1. Studies on Constant-Time Algorithms
for Bounded-Degree Graphs and
Constraint Satisfaction Problems
（次数を制限したグラフと制約充足問題に対する
定数時間アルゴリズムの研究）
京都大学 情報学研究科
通信情報システム専攻
田 悠一
Kyoto University, Japan

2. 研究の背景
• 巨大なデータを扱う必要性
– 例: ゲノム，Web，ユーザログ，天文デー
タ...
• 線形/多項式時間アルゴリズムでさえ遅すぎ
る 計算時間が
入力長nに依存しない
アルゴリズムは作れないか？
Kyoto University, Japan

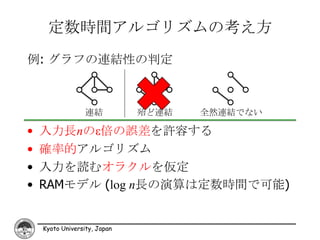
3. 定数時間アルゴリズムの考え方
例: グラフの連結性の判定
連結 殆ど連結 全然連結でない
• 入力長nのε倍の誤差を許容する
• 確率的アルゴリズム
• 入力を読むオラクルを仮定
• RAMモデル (log n長の演算は定数時間で可能)
Kyoto University, Japan

4. 定数時間アルゴリズムとは
定数時間アルゴリズム:
計算時間が入力長nに依存しないアルゴリズム
⋇ εなどのパラメータには依存してよい
先の方針に従って問題を緩和する
• 判定問題 ⇒ 性質検査
• 最適化問題 ⇒ (α, β)近似
Kyoto University, Japan

5. 性質検査
[Blum, Luby Rubinfeld ’93; Rubinfeld, Sudan ’96]
• 判定問題の緩和
• 入力Iが性質Pからε-far:
– I をε割合書き換えないとPを満たさない．
判定問題Pに対するε-検査アルゴリズム
= Pを満たすかε-farかを高い確率で判定
従来: 入力全体 検査: 入力全体 確率2/3
P 受理 P 以上で受理
Pでない 拒否 確率2/3
ε-far 以上で拒否
Kyoto University, Japan

6. (α, β)近似
[Chazelle, Rubinfeld, Trevisan ’05]
• 最適化問題の緩和
• 最適値x*の(α, β)近似 (最大化問題の場合)
αx* - β ≤ x ≤ x*
最適化問題Pに対する(α, β)近似アルゴリズム
= 最適解に対する(α, β)近似を高い確率で出力
本研究の対象:
最適値がO(n)の問題に対する(α, εn)近似
Kyoto University, Japan

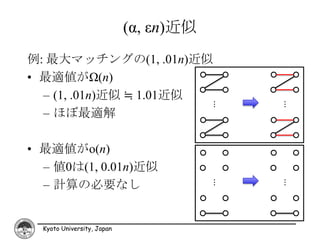
7. (α, εn)近似
例: 最大マッチングの(1, .01n)近似
• 最適値がΩ(n)
– (1, .01n)近似 ≒ 1.01近似
…
…
– ほぼ最適解
• 最適値がo(n)
– 値0は(1, 0.01n)近似
– 計算の必要なし
…
…
Kyoto University, Japan

8. 定数時間アルゴリズムの扱う対象
• 関数
– 線形性 [Blum, Luby, Rubinfeld ’93]
– 低次数多項式 [Rubinfeld, Sudan ’96]
– 確率的検査可能証明(PCP)への応用
• グラフ / 制約充足問題(CSP)
– 密モデル [Goldreich, Goldwasser, Ron ’98]
– 次数制限モデル [Goldreich, Ron ’02]
• 確率分布, 幾何, 形式言語
Kyoto University, Japan

9. 何故，次数制限モデルか
実用的興味: 実世界の多くの問題は疎
理論的興味:
• 密モデルは定数時間アルゴリズムに関して完
結
– 検査可能な性質の必要十分条件 [Alon et al. ’09]
– (1, εn2)近似可能なパラメータの必要十分条
件 [Borgs et al. ’06]
• 密モデルではεn2の誤差を許すため，多くの問
題が自明になる．
– 例: 最大マッチング
Kyoto University, Japan

10. 本研究の目標
対象:
次数制限モデルにおけるグラフと制約充足問題
目標:
定数時間で検査可能 / (α, εn)近似可能な問題の
特徴付け
Kyoto University, Japan

11. グラフに対する次数制限モデル
[Goldreich, Ron ’02]
• d: 次数の上限
• 入力グラフG = (V, E)はオラクル Gで表現
– G(v, i): 頂点vに隣接するi番目の頂点
v
1 3
2
• Gが性質Pからε-far: Pを満たすには少なくと
もεdn本の枝の追加及び削除が必要．
Kyoto University, Japan

12. 既存結果 (グラフ)
• 性質検査
– 連結性, k枝連結性 [Goldreich, Ron ’02]
– k点連結性 [Y., Ito ’08], 外平面性 [Y., Ito ’09]
– H-マイナーフリー [Benjamini et al. ’10]
• (α, εn)近似
– 最小全域木 [Chazelle et al. ’05]
– 頂点被覆 [Parnas, Ron ’07]
– 最大マッチング [Nguyen, Onak ’08]
Kyoto University, Japan

13. 既存結果 (グラフ)
• 枝が少ないと成立しやすい性質
例: 平面グラフ，二部グラフ
ε割合の枝を削除すると，
検査可能 ≒
定数サイズの連結成分に分割可能
[Hassidim et al. ’09; Newman, Sohler ’11]
• 枝が多いと成立しやすい性質
例: 完全マッチングを持つ，k枝連結性
検査可能 ≒ ？
Kyoto University, Japan

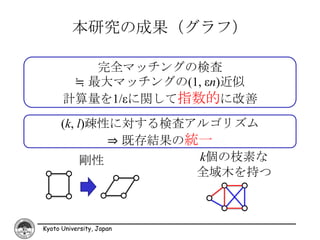
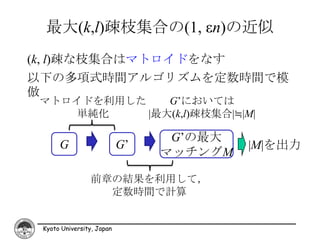
14. 本研究の成果（グラフ）
完全マッチングの検査
≒ 最大マッチングの(1, εn)近似
計算量を1/εに関して指数的に改善
(k, l)疎性に対する検査アルゴリズム
⇒ 既存結果の統一
剛性 k個の枝素な
全域木を持つ
Kyoto University, Japan

15. 制約充足問題 (CSP)
値の集合: L
入力: I = (変数集合V, 制約集合C)
目的: 全制約を満たす変数割り当てを見つける
• 制約の種類により様々な問題になる．
– 線形連立方程式，kSAT，k彩色性
• 次数制限モデル
– オラクル: 変数vを含むi番目の制約を返す
– ε-far: 充足可能にするにはεdn個の制約の削
除が必要
Kyoto University, Japan

16. 既存研究 (CSP)
CSP: 制約が全て充足可能か検査
• Horn SAT: O(1) [Y., Kobayashi ’11]
~
• 2彩色性: Θ(√n) [Goldreich, Ron ’99]
• 3SAT,線形連立方程式: Ω(n) [Bogdanov et al.’02]
Max CSP: 制約を出来るだけ多く充足する
• Max SAT: (2/3, εn)近似 [Trevisan, unpublished]
Kyoto University, Japan

17. 研究の成果（CSP）
定数時間で検査可能なCSPの必要十分条件
Horn SAT ⇒ 検査可能
2SAT，線形連立方程式，3彩色性 ⇒ 検査不可能
全てのCSPに対する最適な
定数時間近似アルゴリズム
例：最大カット
• ∀δ>0，(½, δn)近似は定数時間で可能．
• ∀ε>0∃δ>0，(½+ε,δn)近似は定数時間で不可能．
Kyoto University, Japan

18. 最大マッチングの(1, εn)近似の高速化
Kyoto University, Japan

19. 最大マッチング
• マッチング: 点素な枝の集合
• 以下の貪欲法を考える．
入力：グラフG = (V, E)，枝の順番π
Mπ := ∅
for each e （順番が小さい順に）
if eがMπと頂点を共有しない
Mπ := Mπ + e
return Mπ
[補題] 任意のπに対して，|Mπ| ≧ |M*|/2
M*:最大マッチング
Kyoto University, Japan

20. 最大マッチングの(2, εn)近似
• あるπに対して|Mπ|を定数時間で近似したい
• 以下の様なオラクル πが有ると仮定．
π(e) = [eがMπに含まれる]
F := O(d2/ε2)個のランダムな枝集合
c := FのうちMπに含まれる枝の個数
return cm / |F| m:枝数
[定理] 高い確率でcm / |F|は|Mπ|の(1,εn)近似
⇒ M*の(2, εn)近似
Kyoto University, Japan

21. πの作成
[Nguyen, Onak ’08]
π(e):
res := true
for eに隣接する枝f
if f はeより順番が前 and π(f ) = true
res := false
return res
[Nguyen, Onak ’08]
任意のeに対して，Eπ[ π(e)のクエリ計算量] = 2O(d)
⇒ 計算量2O(d)/ε2の(2,εn)近似アルゴリズム
Kyoto University, Japan

22. πの改良 [本研究]
π(e):
for eに隣接する枝f （小さい順に見る）
if fはeより順番が前 and π(f) = true
return false
return true
[定理] Ee,π[ π(e)のクエリ計算量] = O(d)
⇒ 計算量O(d4/ε2)の(2,εn)近似アルゴリズム
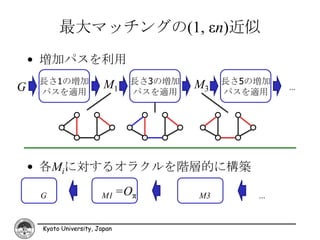
Kyoto University, Japan

23. 最大マッチングの(1, εn)近似
• 増加パスを利用
長さ1の増加 M1 長さ3の増加 M3 長さ5の増加
G パスを適用 パスを適用 パスを適用
...
• 各Miに対するオラクルを階層的に構築
G M1 =Oπ M3 ...
Kyoto University, Japan

24. 最大マッチングの(1, εn)近似
• マッチングM1/εの大きさを近似する
O(1/ε2)
[定理] 最大マッチングに対する計算量 (d/ε)
の(1,εn)近似アルゴリズムが存在
• dO(1/ε) [Nguyen, Onak ’08]から指数的に改善
2
• 最小頂点被覆，最小集合被覆問題でも，指数
的に改善．
Kyoto University, Japan

25. (k, l)疎性に対する検査アルゴリズム
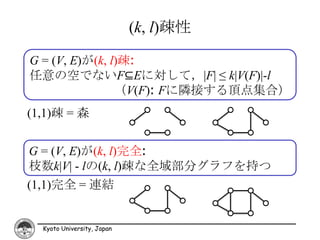
Kyoto University, Japan

26. (k, l)疎性
G = (V, E)が(k, l)疎:
任意の空でないF⊆Eに対して，|F| ≤ k|V(F)|-l
（V(F): Fに隣接する頂点集合）
(1,1)疎 = 森
G = (V, E)が(k, l)完全:
枝数k|V| - lの(k, l)疎な全域部分グラフを持つ
(1,1)完全 = 連結
Kyoto University, Japan

27. (k, l)完全性の検査
[定理] 以下に対する定数時間アルゴリズム
• 最大(k, l)疎枝集合に対する(1,εn)近似
• (k, l)完全性の検査
(1, 1)完全 = 全域木を持つ = 連結
(2, 3)完全 = 剛である
(k, k)完全 = k個の枝素な全域木を持つ
(k, l)完全 = 枝素なl個の全域木とk-l個の全域
(k≥l) 擬似木を持つ
Kyoto University, Japan

28. 最大(k,l)疎枝集合の(1, εn)の近似
(k, l)疎な枝集合はマトロイドをなす
以下の多項式時間アルゴリズムを定数時間で模
倣
マトロイドを利用した G’においては
単純化 |最大(k,l)疎枝集合|≒|M|
G’の最大
G G’ |M|を出力
マッチングM
前章の結果を利用して，
定数時間で計算
Kyoto University, Japan

29. その他の結果
[定理] (k, l)枝連結向き付け可能性は定数時間で
検査可能
• 枝増加問題の手法により証明
• 以前の二つの結果を統一
– k個の枝素な全域木 (l = 0)
– 2k枝連結性 (k = l)
Kyoto University, Japan

30. 全てのCSPに対する
最適な定数時間近似アルゴリズム
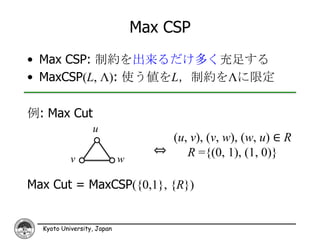
Kyoto University, Japan

31. Max CSP
• Max CSP: 制約を出来るだけ多く充足する
• MaxCSP(L, Λ): 使う値をL，制約をΛに限定
例: Max Cut
u
(u, v), (v, w), (w, u) ∈ R
⇔ R ={(0, 1), (1, 0)}
v w
Max Cut = MaxCSP({0,1}, {R})
Kyoto University, Japan

32. 最適な定数時間近似
[定理] 任意のMaxCSP(L, Λ)に対して、
• ∀δ>0, (α, δn)近似は定数時間で可能
• ∀ε>0,∃δ>0, (α+ε, δn)近似はΩ(n1/2)時間必要
α = BasicLPの整数化ギャップ(∀I, opt(I) ≥ α∙lp(I))
自明 LP W(n1/2)時間
(O(1)時間) (O(1)時間) 必要
一致
Max SAT 0.5 0.75 0.75+ε
Max Cut 0.5 0.5 一致 0.5+ε
一致
Max Dicut 0.25 0.5 0.5+ε
一致
Max k-CSP 1/2k 2/2k 2/2k+ε
Kyoto University, Japan

33. [Raghavendra ’08]との比較
本研究 [Raghavendra ’08]
（定数時間近似） (多項式時間近似)
任意のMax CSPに対し 任意のMax CSPに対し
てBasicLPが最適 てBasicSDPが最適
仮定無しに下限は成立 Unique Games予想
[Khot ’02]の下で下限は成
立
充足可能な入力でも 充足可能な入力では
下限は成立 下限は不成立
Kyoto University, Japan

34. 検査可能なCSPの必要/十分条件
CSP(L, Λ)がBasicLPで判定可能:
lp(I) = 1 ⇒ opt(I) = 1.
CSP(L, Λ)がBasicLPで頑健に判定可能:
lp(I) = 1 – ε ⇒ opt(I) ≥ 1 – r(ε).
r(0) = 0 かつ limε→0r(ε) = 0
[定理]
• CSP(L, Λ)がBasicLPで頑健に判定可能
⇒ 定数時間で検査可能
• 定数時間で検査可能
⇒ CSP(L, Λ)がBasicLPで判定可能
Kyoto University, Japan

35. BasicLP (Max Cutの場合)
μe: 枝eへの割り当ての確率分布
xv: 頂点vへの割り当ての確率分布
μ(u,v)とxu, xvは一貫している
目的関数: Ee Eβ〜μe [β = (0, 1) or (1, 0)]
½⋅ u v + ½⋅ u v = u v
e e
xu xv
μe
Kyoto University, Japan

36. 上限: (α, δn)近似は定数時間で可能
以下の多項式時間アルゴリズムを定数時間で模
倣
I I’
定数サイズ I’の最 Iの近
BasicLP LP解 の入力I’ 適解β’ 似解β
lp(I) ≒ lp(I’) val(I, β) ≒ opt(I’)
⇒ opt(I’) ≥ α⋅lp(I’) ≥ α⋅lp(I)
≒ α⋅lp(I) ≥ α⋅opt(I)
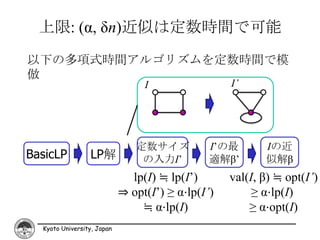
Kyoto University, Japan

37. 下限: (α+ε, δn)近似は定数時間で不可能
• 整数化ギャップ入力Iから二つの入力分布を作
成
入力分布DY : Pr[opt(J) ≥ c] = 1
I J~DY
lp(I) = c 入力分布DN : Pr[opt(J)≤ αc+ε] = 1 – o(1)
opt(I) = αc J~DN
定数時間では分布DYとDNを区別できない
Yao’s Minimax Principle
定数時間では(αΛc+ε, δn)近似できない
Kyoto University, Japan

38. 定数時間で検査可能なCSPに対する
必要十分条件
Kyoto University, Japan

39. 定数時間で検査可能なCSPの特徴付
け
• 検査可能性の組み合わせ的特徴付け
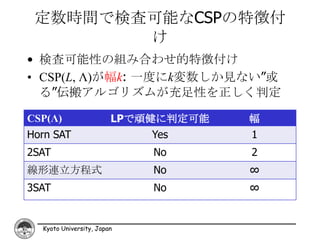
• CSP(L, Λ)が幅k: 一度にk変数しか見ない”或
る”伝搬アルゴリズムが充足性を正しく判定
CSP(Λ) LPで頑健に判定可能 幅
Horn SAT Yes 1
2SAT No 2
線形連立方程式 No ∞
3SAT No ∞
Kyoto University, Japan

40. 定数時間で検査可能なCSPの特徴付
け
[定理]
幅1 ⇒ BasicLPで頑健に判定可能 [本研究]
BasicLPで判定可能 ⇒ 幅1
⊆
[Kun, O’Donnell, Tamaki, Y., Zhou ’12]
BasicLPで頑健に判定可能 ⇒定数時間検査可能
定数時間で検査可能 ⇒ BasicLPで判定可能
[系] CSP(L, Λ)が定数時間で検査可能
if and only if
CSP(L, Λ)が幅1
Kyoto University, Japan

41. 今後の課題（グラフ）
• 検査可能な性質の特徴付けの完成
• 枝が多いほど成り立ちやすい性質
– k枝連結性，k点連結性，(k, l)疎性，(k, l)枝
連結度向き付け可能性
– 枝増加問題で統一的に説明出来る？
– 枝の追加と縮約に関して閉じている性質は
全て検査可能？
Kyoto University, Japan

42. 今後の課題（CSP）
• 定数時間アルゴリズムに関してはほぼ完結
• 準線形時間アルゴリズム
– 二部グラフ: Õ(√n)クエリで検査可能，幅３
– 線形連立方程式: Ω(n)クエリ必要，幅∞
– 凖線形時間で検査可能 ⇔ 幅3？
– 2SATの検査のクエリ計算量？
Kyoto University, Japan