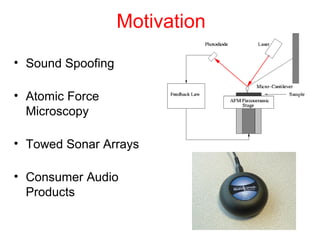
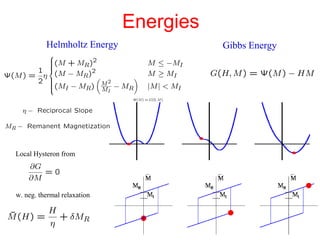
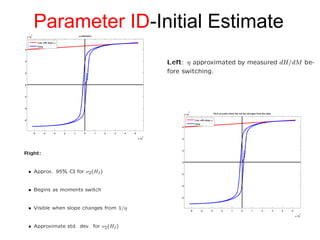
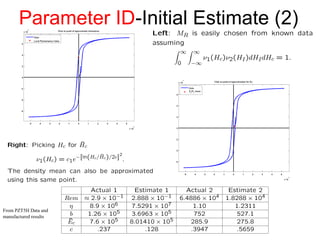
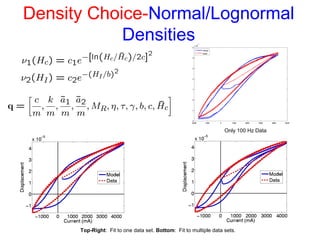
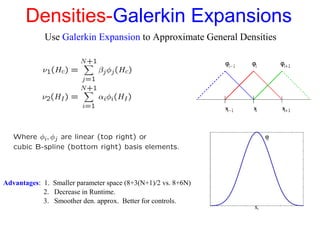
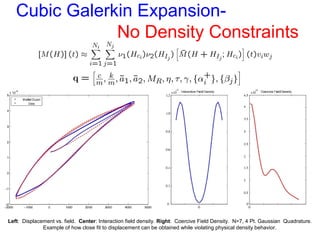
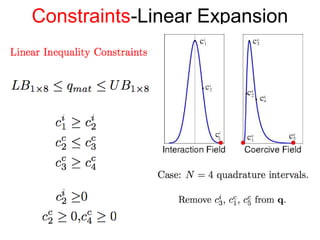
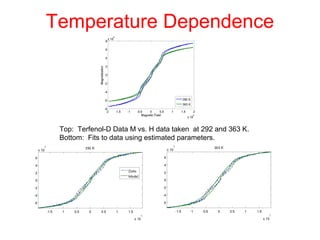
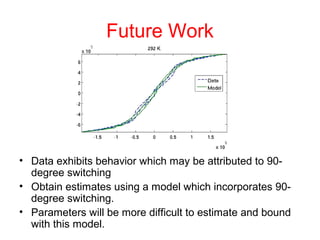
The document presents an overview of a preliminary oral exam focusing on the modeling, parameter estimation, and optimization of an active machining system using terfenol-D. Key aspects include the development of accurate models and controllers, parameter estimation techniques, temperature dependence of materials, and future directions for improving estimation routines. The conclusions highlight the dissipation and efficiency of the modeling approach, while future work aims to enhance initial estimates and explore constraints on density behavior.

1. Oral Preliminary Exam
Jon Ernstberger
Advisor: Ralph C. Smith
April 5, 2007

2. Outline
• Motivation
• Model Description
• Past Work
• Parameter Estimation for the AMS
• Conclusions
• Future Work

3. Motivation-Active Machining System
• ETREMA Products, Inc.
• Active Mat.: Terfenol-D
• High-Speed Milling
(4,000 RPM)
Courtesy of http://www.etrema-usa.com/

4. Motivation
• Sound Spoofing
• Atomic Force
Microscopy
• Towed Sonar Arrays
• Consumer Audio
Products

5. Introduction to Model
• Know Terfenol-D exhibits a physical
lengthening in response to magnetic field.
• Goal is to implement accurate controller in
the use of machining.
• Requires an accurate model representation.
• Need to model how rod tip displacement
(assume uniform strain) varies nonlinearly in
response to magnetic field.

6. Energies
Gibbs EnergyHelmholtz Energy
w. neg. thermal relaxation
Local Hysteron from

7. Thermal Relaxation
Moment Fraction Evolution:
Local Avg. Magnetization:
Expected Magnetization:
Switching Likelihood:
Boltzmann Relation:

8. Homogenized Energy Model
Subject to:
Where:

9. Dissipativity of HEM
• If a system is dissipative, it loses energy.
• “The energy at final time is less than or equal to
initial energy plus input energy.”
• Showed dissipativity of
– Preisach model
– HEM with negligible thermal relaxation for supply rates
and
– HEM with thermal relaxation for same supply rates
• Statement of stability and helps design controllers
HM MH 

10. Lumped Rod Model
Balance rod forces σA with restoring mechanism
or

11. Previous Work and Future Directions
• Prior work
– Homogenized Energy and Lumped Rod Model
– Parameter Estimation with HEM using normal/lognormal
and general densities.
– Modeling of temperature dependence.
• Direction
– Drastically reduce parameter estimation time for the
HEM/LRM.
– Enforce density shapes and incorporate modeling of
physical behaviors.
– Deliver a nearly black box parameter estimation routine.

12. Parameter ID-Initial Estimate

13. Parameter ID-Initial Estimate (2)
From PZT5H Data and
manufactured results

14. Density Choice-Normal/Lognormal
Densities
Only 100 Hz Data
Top-Right: Fit to one data set. Bottom: Fit to multiple data sets.

15. Densities-Galerkin Expansions
Use Galerkin Expansion to Approximate General Densities
Advantages: 1. Smaller parameter space (8+3(N+1)/2 vs. 8+6N)
2. Decrease in Runtime.
3. Smoother den. approx. Better for controls.

16. Cubic Galerkin Expansion-
No Density Constraints
Left: Displacement vs. field. Center: Interaction field density. Right: Coercive Field Density. N=7, 4 Pt. Gaussian Quadrature.
Example of how close fit to displacement can be obtained while violating physical density behavior.

17. Constraints-Linear Expansion

18. Sequential Quadratic Programming
Newton Update:
QP
Subproblem:
Constrained
Optimization
Problem:

19. Results-SQP/SQP
100 Hz 200 Hz
300 Hz 500 Hz
•N=8 Intervals
•4 Pt. Gauss. Quad.
•Linear Expansion
•2000 SQP Fcn Evals
•Runtime: 164.7s

20. Genetic Algorithms
1. Initialize
Population
1. Evaluate
Population
1. Iterate
a. Select
b. Crossover
c. Mutate
d. Evaluate
Algorithm:

21. Fix-Seeded GA
• Normal/
Lognormal used
to seed GA
• Ran enough
iterations to get
close to a local
minima.

22. Results-SQP/GA/SQP
100 Hz 200 Hz
300 Hz 500 Hz
•N=8 Intervals
•Linear Expansion
•4pt. Gauss. Quad.
•250 GA Generations/
33250 Fcn Evals
•1000 SQP Fcn Evals
•Runtime 2,449.3s
•No Crossover

23. Simulated Annealing
Boltzmann Distribution:
Ratio:

24. Results: SQP-SA
100 Hz 200 Hz
300 Hz 500 Hz
•N=8
•4-Pt. Gauss. Quad.
•Many fcn evals
•Soft constraints

25. Alternate Optimization Routines
• Differential Evolution
– Evolution Alg./No initial population
– Only simple constraint bounds (upper,lower)
– Creates new population by differencing
alternate members and adding other member.
• Patternsearch
– Direct Search/initial population
– Allows for constraints
– Choose optimal search via a specified
pattern.

26. Temperature Dependence
Terfenol-D behavior as temperature rises:
• Reduction of saturation magnetization
• Decrease in hysteresis in H-M relation
• Change to anhysteretic H-M relation
through the freezing temperature
How may we incorporate this behavior into
the HEM for ferromagnetics?

27. Temperature Dependence
Using a Helmholtz Energy which incorporates Temperature
from which are yielded
through the relation

28. Temperature Dependence
Top: Terfenol-D Data M vs. H data taken at 292 and 363 K.
Bottom: Fits to data using estimated parameters.

29. Conclusions
• Showed the HEM to be dissipative.
• Greatly reduced the time required to
perform accurate parameter estimation.
• Begin optimization with more accurate
initial estimates (in some cases).
• Constrained densities to have quasi-
physical characteristics.
• Incorporated temperature dependence
into model.

30. Future Work
• Investigate external optimization routines
(donlp2 and NLPQLP)
– Current Model Evaluations is a C implementation.
– MATLAB interface for optimization routine comes
at a cost of function handles, calls, and passes.
– Data sorting occurs at every model call.
– Preliminary results support the robustness of
several of these “industrial-grade” solvers.

31. Future Work
• Obtain better initial parameter estimates
– We can obtain good initial estimates for HEM
given magnetization vs. field data.
– Can we obtain LRM parameters given strain
and magnetization data?
– Can we obtain model parameters if only given
strain vs. field data?

32. Future Work
• Data exhibits behavior which may be attributed to 90-
degree switching
• Obtain estimates using a model which incorporates 90-
degree switching.
• Parameters will be more difficult to estimate and bound
with this model.

33. Future Work
• In too many cases, we’ve had to use
constraints to enforce desired density
behavior.
– Identify other densities which do not require
these bulk constraints.
– Hope to reduce number of parameters to
estimate for densities.

34. Future Work
• Combine work into black-box parameter
estimation scheme for the AMS.
– This work must be executable on the AMS
when delivered.
– "Hands- off" implementation required for
general users.

35. References
[1] P.T. Boggs and J.W. Tolle. Sequential quadratic programming for large-scale
nonlinear optimization. Journal of Computational and Applied Mathematics, 124(1-
2):123–137, 2000.
[2] A.R. Conn, N. Gould, and P.L. Toint. A Globally Convergent Lagrangian Barrier
Algorithm for Optimization with General Inequality Constraints and Simple Bounds.
Mathematics of Computation, 66(217):261–288, 1997.
[3] J.H. Holland. Genetic algorithms and the optimal allocation of trials. SIAM Journal
of Computing, 2(2), 1973.
[4] C.T. Kelley. Iterative Methods for Optimization. Society for Industrial and Applied
Mathematics, 3600 University Science Center, Philadelphia, PA 19104-2688, 1999.
[5] R.M. Lewis and V. Torczon. Pattern search algorithms for bound constrained
minimization. SIAM Journal on Optimization, 9(4):1082–1099, 1999.

36. [6] R.M. Lewis and V. Torczon. A globally convergent augmented lagrangian pattern
search algorithm for optimization with general constraints and simple bounds. SIAM
Journal on Optimization, 12(4):1075–1089, 2002.
[7] Mitchell M. An Introduction to Genetic Algorithms. The MIT Press, Cambridge,
MA, London, England,1996.
[8] N. Metropolis, A.W. Rosenbluth, M.N. Rosenbluth, and A.H Teller. Equation of
State Calculations by Fast Computing Machines. The Journal of Chemical Physics,
21(6):1087–1092, 1953.
[9] M. Momma and K.P. Bennett. A pattern search method for model selection of
support vector regression. Proceedings of the SIAM International Conference on
Data Mining, pages 261–274, 2002.
[10] R.C. Smith. Smart Material Systems: Model Development. Society for Industrial
and Applied Mathematics, 2005.
[11] R.C. Smith, A.G. Hatch, T. De, M.V. Salapaka, R.C.H. del Rosario, and J.K.
Raye. Model development for atomic force microscope stage mechanisms. SIAM
Journal on Applied Mathematics, 66(6):1998–2026,2006.

37. [12] J.C. Spall. Introduction to Stochastic Search and Optimization: Estimation,
Simulation and Control. John Wiley and Sons, Inc., 2003.
[13] R. Storn. On the Usage of Differential Evolution for Function Optimization. do,
50:0.
[14] R. Storn and K. Price. Differential evolution-a simple and efficient adaptive
scheme for global optimization over continuous spaces. Journal of Global
Optimization, 11(4):341–359, 1997.
[15] J. M. Ernstberger and R. C. Smith. High-speed parameter estimation for
nonlinear smart materials. Modeling, Signal Processing, and Control for Smart
Structures 2007. Edited by Lindner, Douglas K. Proceedings of the SPIE. 6523,
2007.