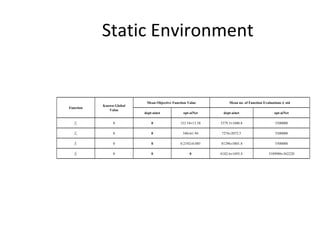
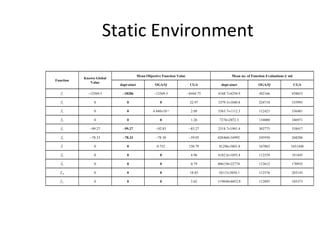
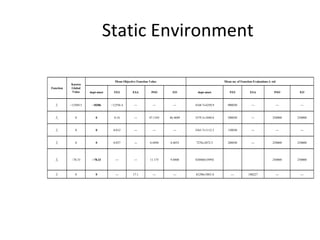
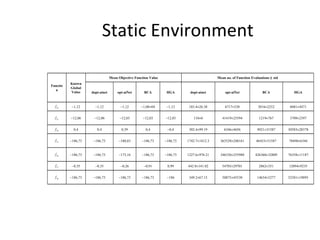
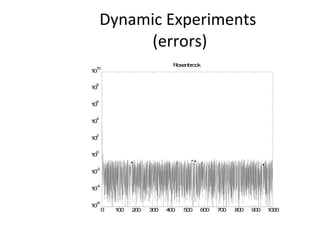
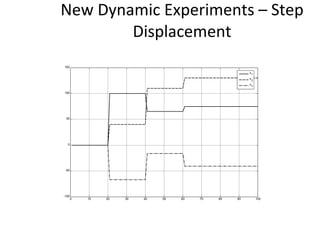
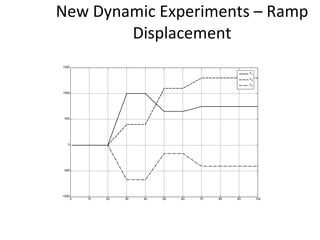
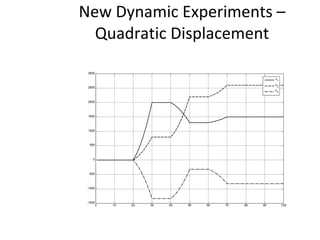
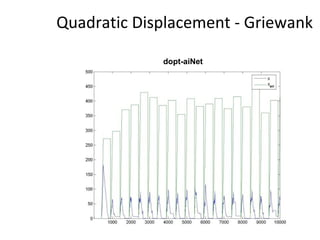
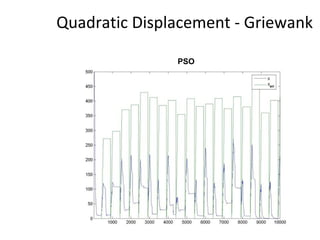
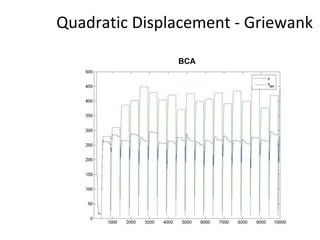
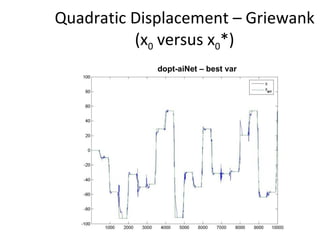
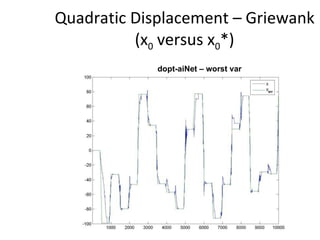
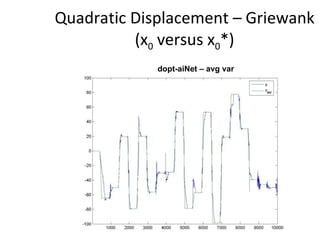
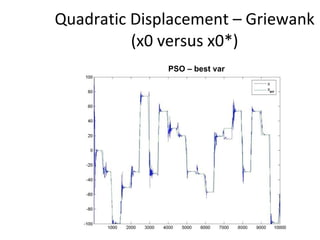
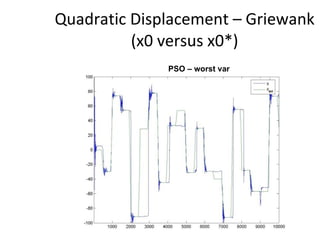
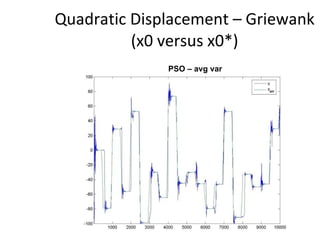
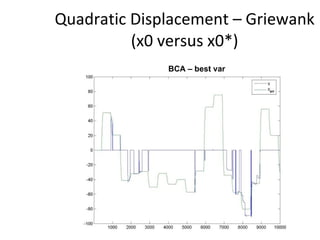
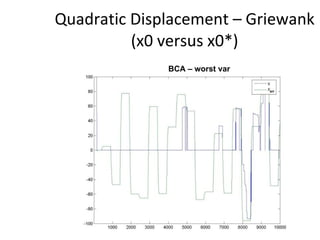
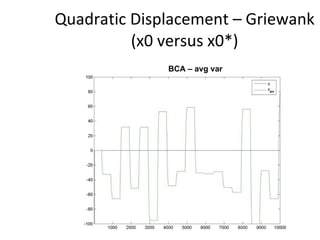
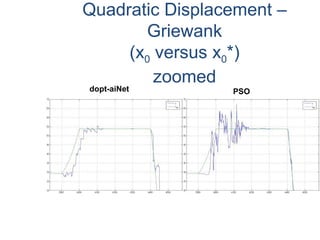
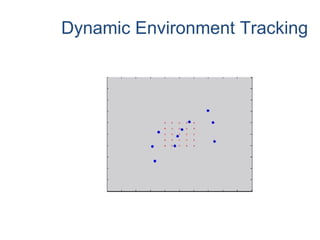
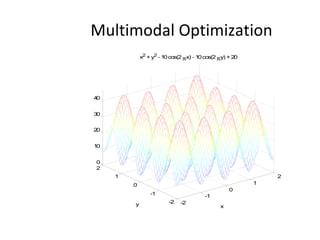
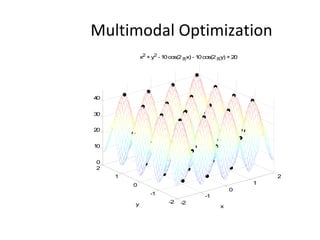
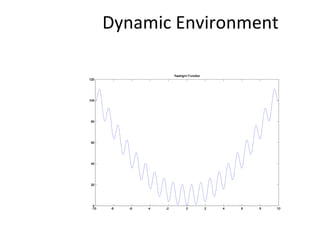
The document proposes an artificial immune network called dopt-aiNet for solving multimodal optimization problems in dynamic environments. dopt-aiNet is inspired by the immune system and uses clonal selection, mutation, and suppression techniques to maintain diversity and track moving optima. Numerical experiments show that dopt-aiNet outperforms other algorithms in terms of accuracy, convergence speed, and ability to track changing optima using fewer function evaluations. The paper discusses areas for future work such as improving suppression algorithms and studying the impact of different mutation operators.

1. An Artificial Immune Network for Multimodal Function Optimization on Dynamic Environments Fabricio Olivetti de França LBiC/DCA/FEEC State University of Campinas (Unicamp) PO Box 6101, 13083-970 Campinas/SP, Brazil Phone: +55 19 3788-3885 [email_address] Fernando J. Von Zuben LBiC/DCA/FEEC State University of Campinas (Unicamp) PO Box 6101, 13083-970 Campinas/SP, Brazil Phone: +55 19 3788-3885 [email_address] Leandro Nunes de Castro Research and Graduate Program in Computer Science, Catholic University of Santos, Brazil. Phone/Fax: +55 13 3226 0500 [email_address]

2. Multimodal Optimization Most algorithms seek only for one optima, hopefully the global one. But maintaining a diversity of local optima solutions helps to improve the whole population solution by not allowing new elements on an already explored neighborhood

3. Multimodal Optimization

4. Multimodal Optimization

5. Local Search Algorithms Converges to nearest Local Optima Usually requires derivative information about the function

6. Meta-heuristics Strategies that defines heuristics to solve a problem, the most successful strategies for non-linear optimization are population based algorithms as it tries several optimas at the same time. Evolutive Strategies Genetic Algorithms opt-aiNet dopt-aiNet

7. Immuno-inspired Algorithms Usually the strategy of populational algorithms is to initially scatter all the individuals on the search space and to make them to converge to a common point where it resides the best local optima found. Exploitation and Exploration

8. Immuno-inspired Algorithms Immuno-inspired algorithms (i.e.: dopt-aiNet) innovates by not allowing two population individuals to converge to the same point. (exploration). Local search of an individual neighborhood (exploitation) is made through clonal selection

9. Immuno-inspired Algorithms Cell populations are represented by a vector of real numbers Cloning process Mutation Clonal Selection Diversity Control through cells affinity

10. opt-aiNet A population of points in n-dimensional Euclidian space are created and each one will be responsible for exploring its vicinity

11. opt-aiNet The exploration process is made by cloning each individual e mutating each clone “c” as:

12. Disadvantage The user must set a constant β a priori, and this value is not optimal at most times

13. Solution Introduce a line search algorithm to estimate the best value for  .

14. Line Search: Golden Section Given a search direction “D” find the step  the minimizes f(x+  .D). If the interval “I” on this function is unimodal and convex one can easily find the best step size by sub-dividing this interval until converges to the optima.

15. But…

16. … what should go here…

17. … may land here

18. How to deal with it Sub-dividing the search into n intervals may reduce de possibility of a failure Also, if it happens just one failure on a population of Nc clones it may not be much troublesome

19. Another mutation disadvantage The possible directions are restricted to gaussian probabilities. When the function has a great number of variables the direction vector generated tends to have 50% of its size with positive values and 50% negative.

20. Solution New mutations are created in order to allow a clone to search most neighborhood.

21. One Dimensional Mutation The search direction is: D =

22. Gene Duplication This creates a brand new cell.

23. Suppression As stated earlier the main goal of opt-aiNet is to maintain diversity on its population. In order to do this when two cells reside on the same vicinity, the one with worst objective function value must be cut off.

24. opt-aiNet It is measured the Euclidian distance of the cells, and if this distance is equal or less than a threshold value the worst cell dies.

25. problem

26. Solution: Cell-line Suppression

27. Solution: Cell-line Suppression

28. Solution: Cell-line Suppression

29. Nothing is Perfect

30. Solution Only compare the closest points in order to reduce the chance of a failure occurrence.

31. Waste of Memory In functions with many peaks opt-aiNet population size grows exponentially and the computational resource wasted may be just an useless effort.

32. Two Solutions The most obvious: to limit the population size to an upper bound, not allowing more than a certain number of individuals. If the size reach this number the worst elements are eliminated.

33. Two Solutions The other solution, more robust, is to implement a second population called “Memory Cells” where a given cell that does not improve its solution for a certain time period is assumed to have converged and put into this population where no more mutation will be done.

34. Two Solutions Initially each cell is given a rank value and whenever this cells succeeds to improve after a mutation operation this value is incremented, otherwise it is decremented. When this value reaches zero the cell is assumed to have converged.

35. dopt-aiNet These improvements altogether form a new algorithm called dopt-aiNet (artificial immune network for dynamic optimization).

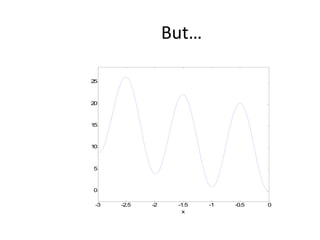
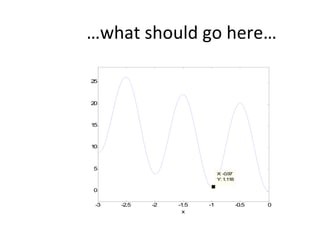
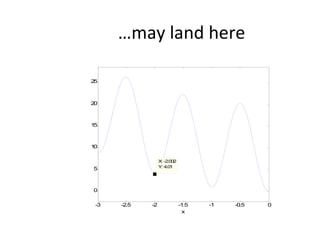
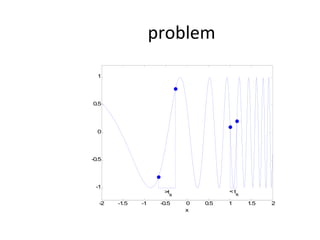
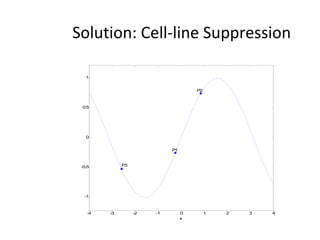
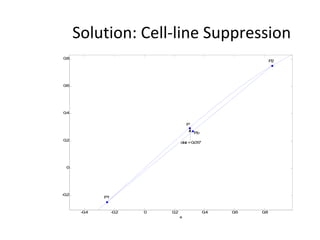
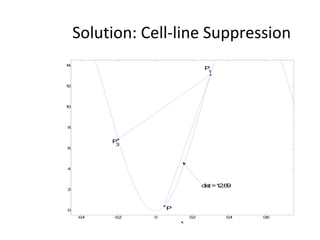
36. dopt-aiNet Function [C] = dopt-aiNet(Nc,range, σ s,f,max_cells) C = random(range) While stopping criterion is not met do fit = f(C) C’ = clone(C,Nc) C’ = mutate(C’,f) C’ = one-dimensional(C’,f) C = clonal_selection(C,C’); C = gene_duplication(C,f) For each cell c from C do , If c’ is better than c, c.rank = c.rank + 1 c = c’ Else c.rank = c.rank – 1 End If c.rank == 0, Mem = [Mem, c] End End Avg = average(f(C)) If the average error does not stagnate return to the beginning of the loop else cell_line_suppress(C, σ s) C = [C; random(range)] End If size(C) > max_cells, suppress_fitness(C) End End End

37. What makes an algorithm able to solve dynamic problems? The capability to: Maintain diversity Escape from local optima dopt-aiNet is capable of both

38. Dynamic Environment Type I: Type II: Type III: Type IV: Marco Farina, Kalyanmoy Deb, Paolo Amato: Dynamic Multiobjective Optimization Problems: Test Cases, Approximation, and Applications . EMO 2003: 311-326

39. Dynamic Environment

40. Type I

41. Type II

42. Type III

43. Type IV

44. dopt-aiNet Advantages between dopt-aiNet and others optimization algorithms: Fast convergence to the local optima nearest to each cell; On average, it needs less function evaluations to reach the global optima on toy functions; Can successfully maintain diversity discovering earlier when two cells are bound to the same optima, and with low error rate; Fast reaction capacity as the environment changes. Self-adjusted population size avoiding computational waste.

45. Numerical Experiments

46. Numerical Experiments

47. Numerical Experiments

48. Numerical Experiments Function Initialization Range Problem Dimension (N) f 1 [-500, 500] N 30 f 2 [-5.12, 5.12] N 30 f 3 [-32, 32] N 30 f 4 [-600, 600] N 30 f 5 [0,  ] N 30 f 6 [-5, 5] N 100 f 7 [-5, 10] N 30 f 8 [-100, 100] N 30 f 9 [-10, 10] N 30 f 10 [-100, 100] N 30 f 11 [-100, 100] N 30

49. Static Environment Function Known Global Value Mean Objective Function Value Mean no. of Function Evaluations  std dopt-ainet opt-aiNet dopt-ainet opt-aiNet f 2 0 0 153.54±13.58 3379.3±1040.8 5500000 f 4 0 0 340±61.94 7276±2072.5 5500000 f 7 0 0 0.2192±0.085 81296±5801.8 5500000 f 8 0 0 0 6182.6±1693.4 3109986±362220

50. Static Environment Function Known Global Value Mean Objective Function Value Mean no. of Function Evaluations  std dopt-ainet OGA/Q CGA dopt-ainet OGA/Q CGA f 1  12569.5  18286  12569.5  8444.75 4168.7±4250.9 302166 458653 f 2 0 0 0 22.97 3379.3±1040.8 224710 335993 f 3 0 0 4.440  10  6 2.69 5563.7±1112.3 112421 336481 f 4 0 0 0 1.26 7276±2072.5 134000 346971 f 5  99.27  99.27  92.83  83.27 2318.7±1901.4 302773 338417 f 6  78.33  78.33  78.30  59.05 428460±34992 245930 268286 f 7 0 0 0.752 150.79 81296±5801.8 167863 1651448 f 8 0 0 0 4.96 6182.6±1693.4 112559 181445 f 9 0 0 0 0.79 406150±22774 112612 170955 f 10 0 0 0 18.83 10113±3050.1 112576 203143 f 11 0 0 0 2.62 119840±6052.8 112893 185373

51. Static Environment Function Known Global Value Mean Objective Function Value Mean no. of Function Evaluations  std dopt-ainet FES ESA PSO EO dopt-ainet FES ESA PSO EO f 1  12569.5  18286  12556.4 --- --- --- 4168.7±4250.9 900030 --- --- --- f 2 0 0 0.16 --- 47.1345 46.4689 3379.3±1040.8 500030 --- 250000 250000 f 3 0 0 0.012 --- --- --- 5563.7±1112.3 150030 --- --- --- f 4 0 0 0.037 --- 0.4498 0.4033 7276±2072.5 200030 --- 250000 250000 f 6  78.33  78.33 --- --- 11.175 9.8808 428460  34992 250000 250000 f 7 0 0 --- 17.1 --- --- 81296±5801.8 --- 188227 --- ---

52. Static Environment Function Known Global Value Mean Objective Function Value Mean no. of Function Evaluations  std dopt-ainet opt-aiNet BCA HGA dopt-ainet opt-aiNet BCA HGA f 12  1,12  1,12  1,12  1,08±04  1,12 103.4±26.38 6717±538 3016±2252 6081±4471 f 13  12,06  12,06  12,03  12,03  12,03 110±0 41419±25594 1219±767 3709±2397 f 14 0,4 0,4 0,39 0,4  0,4 302.4±99.19 6346±4656 4921±31587 30583±28378 f 15  186,73  186,73  180,83  186,73  186,73 1742.7±1412.3 363528±248161 46433±31587 78490±6344 f 16  186,73  186,73  173,16  186,73  186,73 1227.6±976.21 346330±255980 426360±32809 76358±11187 f 17  0,35  0,35  0,26  0,91 0,99 442.8±141.82 54703±29701 2862±351 12894±9235 f 18  186,73  186,73  186,73  186,73  186 349.2±67.15 50875±45530 14654±5277 52581±19095

53. Dynamic Experiments Type I. Three types of optima displacement.  k =  k +   k =  k + N (1,0) (b) Circular (c) Gaussian (a) Linear

54. Dynamic Experiments (errors)

55. Dynamic Experiments (errors)

56. Dynamic Experiments (errors)

57. Dynamic Experiments (errors)

58. New Dynamic Experiments – Step Displacement

59. New Dynamic Experiments – Ramp Displacement

60. New Dynamic Experiments – Quadratic Displacement

61. Quadratic Displacement - Griewank dopt-aiNet

62. Quadratic Displacement - Griewank PSO

63. Quadratic Displacement - Griewank BCA

64. Quadratic Displacement – Griewank (x 0 versus x 0 *) dopt-aiNet – best var

65. Quadratic Displacement – Griewank (x 0 versus x 0 *) dopt-aiNet – worst var

66. Quadratic Displacement – Griewank (x 0 versus x 0 *) dopt-aiNet – avg var

67. Quadratic Displacement – Griewank (x0 versus x0*) PSO – best var

68. Quadratic Displacement – Griewank (x0 versus x0*) PSO – worst var

69. Quadratic Displacement – Griewank (x0 versus x0*) PSO – avg var

70. Quadratic Displacement – Griewank (x0 versus x0*) BCA – best var

71. Quadratic Displacement – Griewank (x0 versus x0*) BCA – worst var

72. Quadratic Displacement – Griewank (x0 versus x0*) BCA – avg var

73. dopt-aiNet PSO Quadratic Displacement – Griewank (x 0 versus x 0 *) zoomed

74. Dynamic Environment Tracking

75. Conclusion: advantages of dopt-aiNet More stability when of occurrence of changes on the environment dopt-aiNet can track a moving target faster than the other algorithms. Capacity to identify multiples optima maintaining several “cells” on strategic positions Although its performance per iteration is usually worse than other algorithms it needs much lesser iterations to reach the optimum, and so the total number of function evaluations needed is much less.

76. Future Work The need to test every pair of cells on suppression algorithm The best moment to do the above procedure avoiding cpu waste Use the absolute value on distance measure between the line and the point. Gaussian mutation combined with one-dimensional mutation An accurate study of how significant each new operator is on improving the algorithm

77. Discussions