The document discusses the optimization of classroom scheduling at LaGrange College and presents a genetic algorithm-inspired approach for solving scheduling problems. The current scheduling system has limitations, such as class size and professor availability, and aims to improve efficiency through a custom integer-based genetic algorithm. The results indicate that while progress has been made, there are still errors in the scheduling, signaling the need for further refinement and potential future enhancements.

1. Optimized Classroom Scheduling at LaGrange
College
Jon M. Ernstberger
21 March 2016

2. About LaGrange College

3. About LaGrange College

4. About LaGrange College

5. We are growing.

6. Classroom Assignment
Heres how this process currently works:
Departments know which courses must run in a given term.
Knowing familial responsibilities, chairs make teaching
schedules.
Everyone tries to schedule in their own building.
Priority is given to largest classes.

7. Simple Case
A builidng with two rooms and only three MWF scheduling periods.
Period No. Room 1 Room 2
One
Two
Three
You have six scheduling opportunities.

8. Simple Case
Call each of those spaces a “bin”.
Period No. Room 1 Room 2
One 1 2
Two 3 4
Three 5 6
What if you only have four classes and two professors?

9. Metaheuristic Approach - Inspired by Genetic Algorithm
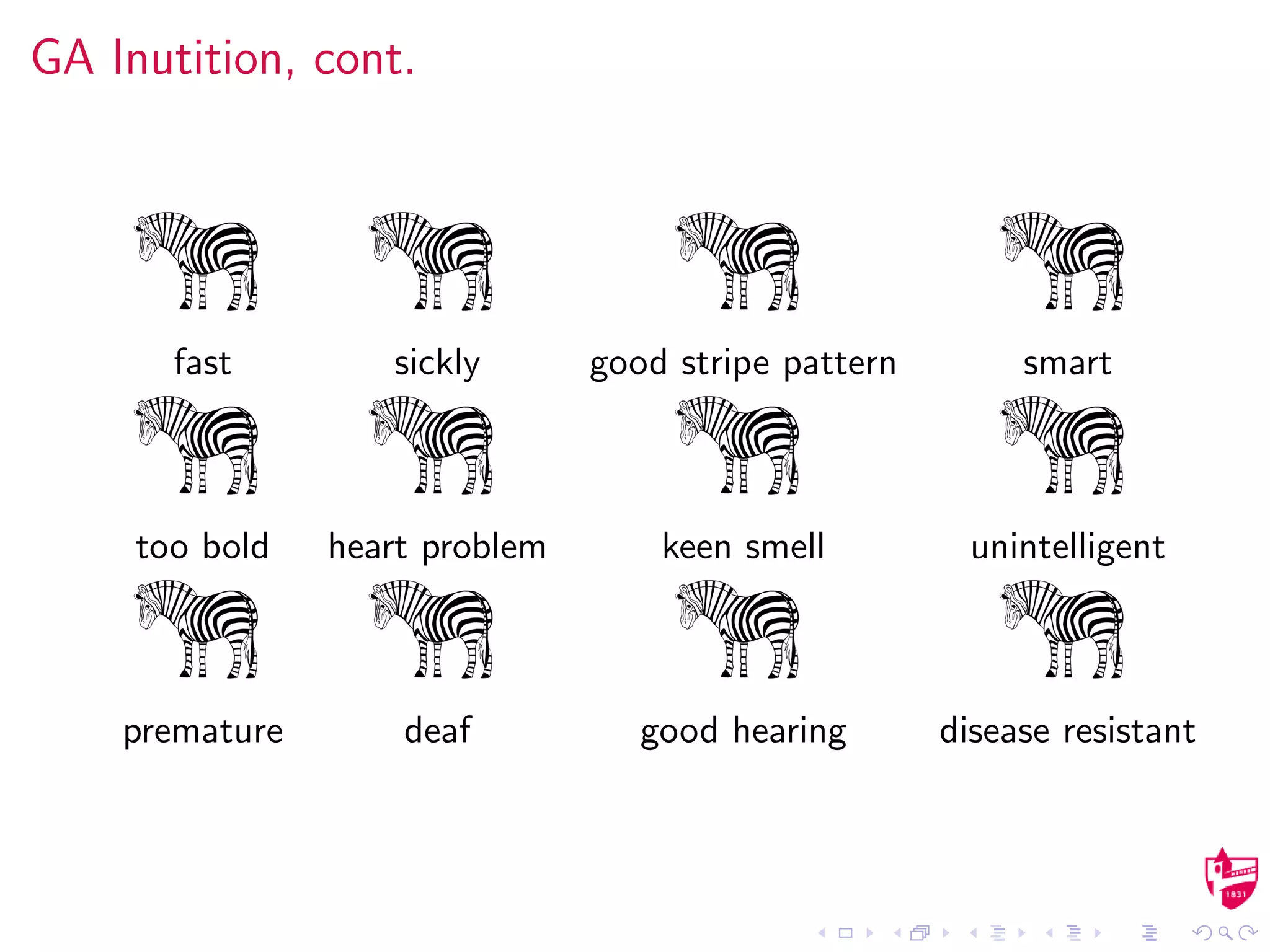
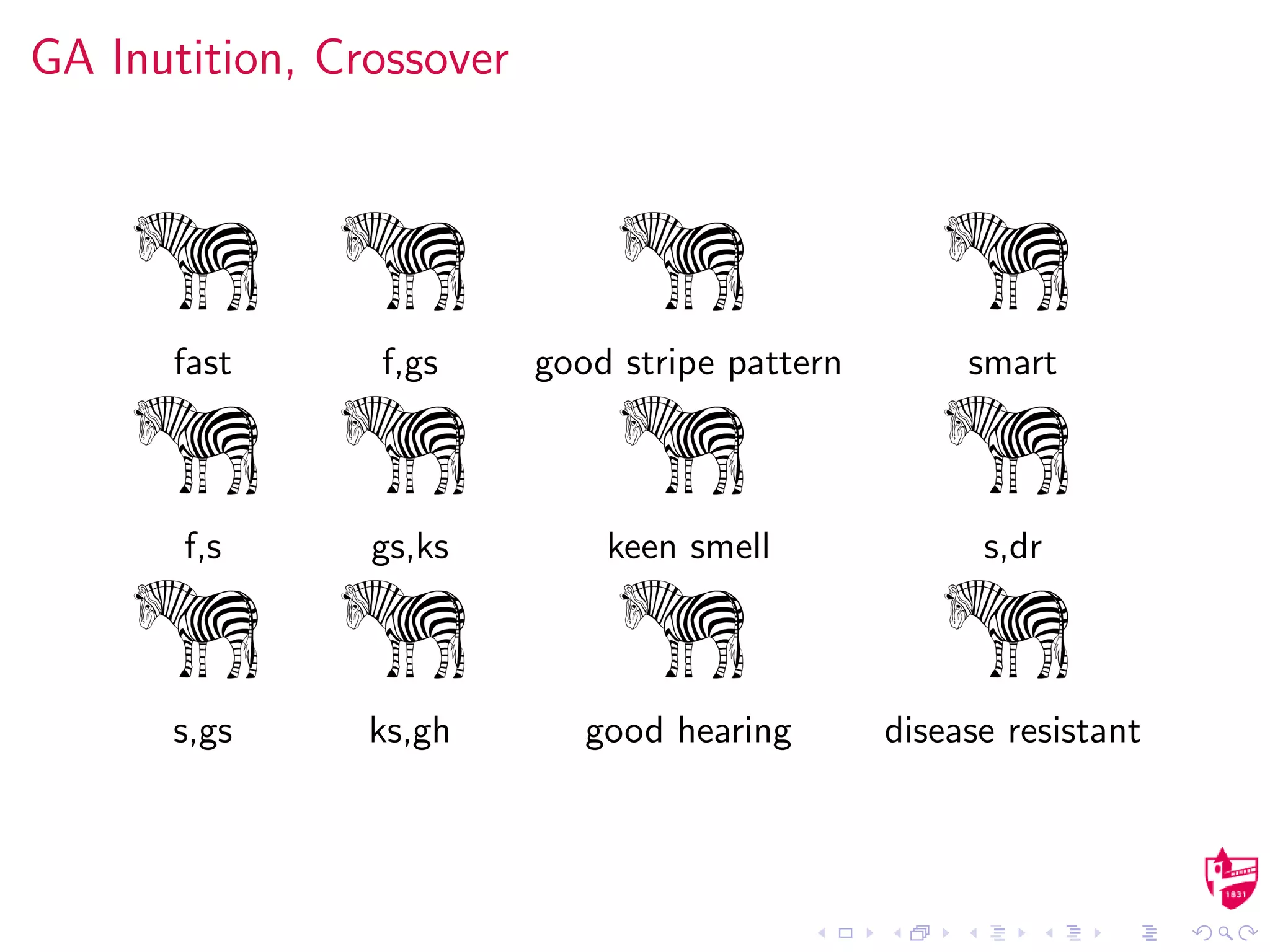
Holland[1] defines this concept of a genetic algorithm.
A population P of trial solutions is randomly created, typically
in Rm×n – m “solutions” for a problem whose domain is in
Rn(a, b).
A fitness function is defined so that the goodness-of-fit of
each member (possible solution) is measured.
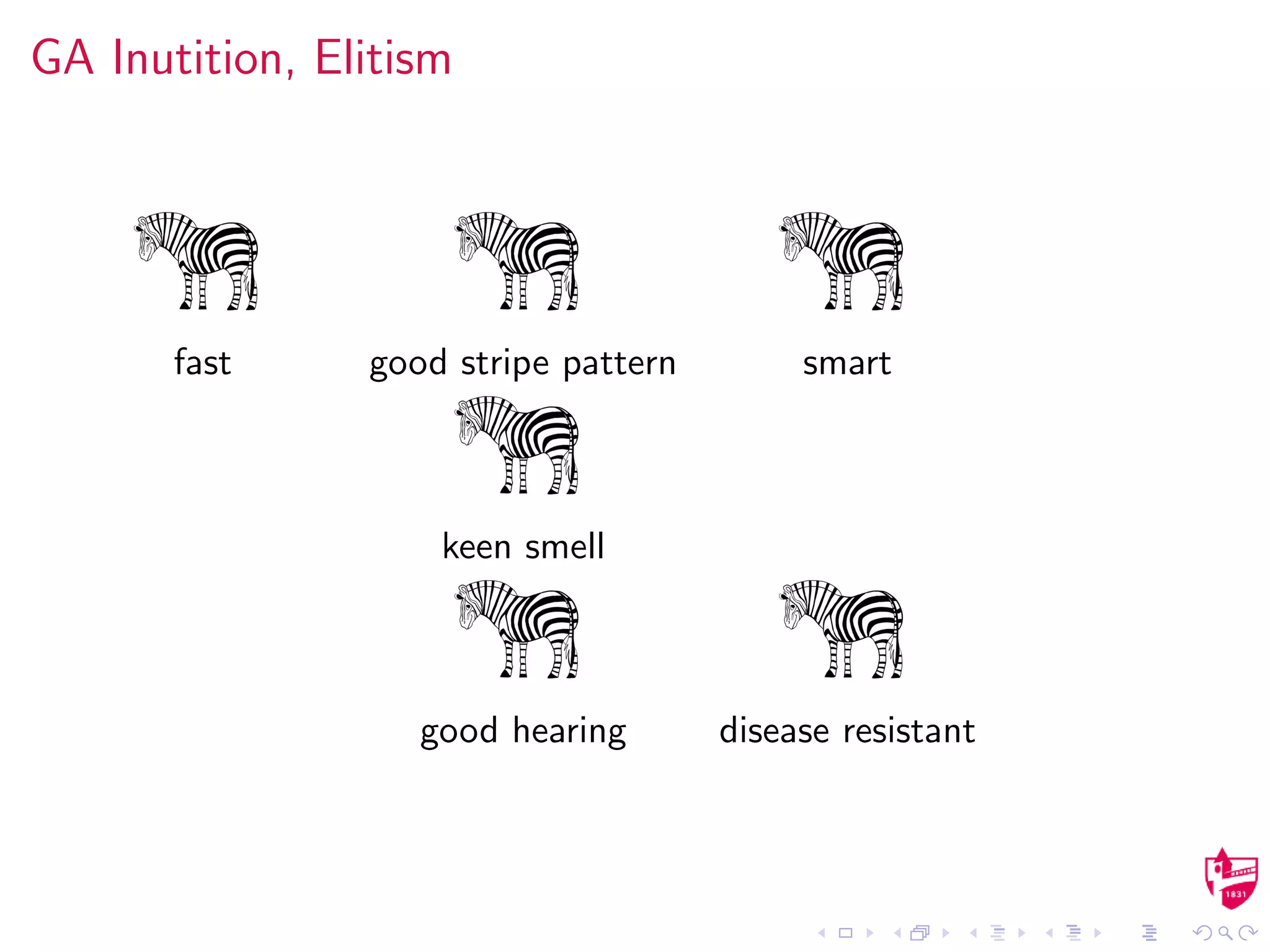
Those solutions deemed most fit remain until a new
“generation”. This process is known as elitism.
Offspring are created via the two processes mutation and
crossover.
Mutation is the result of random noise being added to a
population (or individual attributes, the genes).
Crossover occurs with a probability p and is a direct swap
between genes.

10. GA Intuition

11. GA Inutition, cont.

12. GA Inutition, cont.
fast sickly good stripe pattern smart
too bold heart problem keen smell unintelligent
premature deaf good hearing disease resistant

13. GA Inutition, Elitism
fast good stripe pattern smart
keen smell
good hearing disease resistant

14. GA Inutition, Crossover
fast f,gs good stripe pattern smart
f,s gs,ks keen smell s,dr
s,gs ks,gh good hearing disease resistant

15. GA Inutition, Crossover and Mutation
fast f+
,gs good stripe pattern smart
f,s− gs−,ks−
keen smell s−,dr+
s+,gs+ ks+
,gh−
good hearing disease resistant

16. #GAProbz
There is no formal theory for the convergence (or lack
thereof) of the genetic algorithm.
The algorithm cannot state definitively that there is no
optimized classroom schedule.
It could be fast or it could be slow.
Computationally intense.

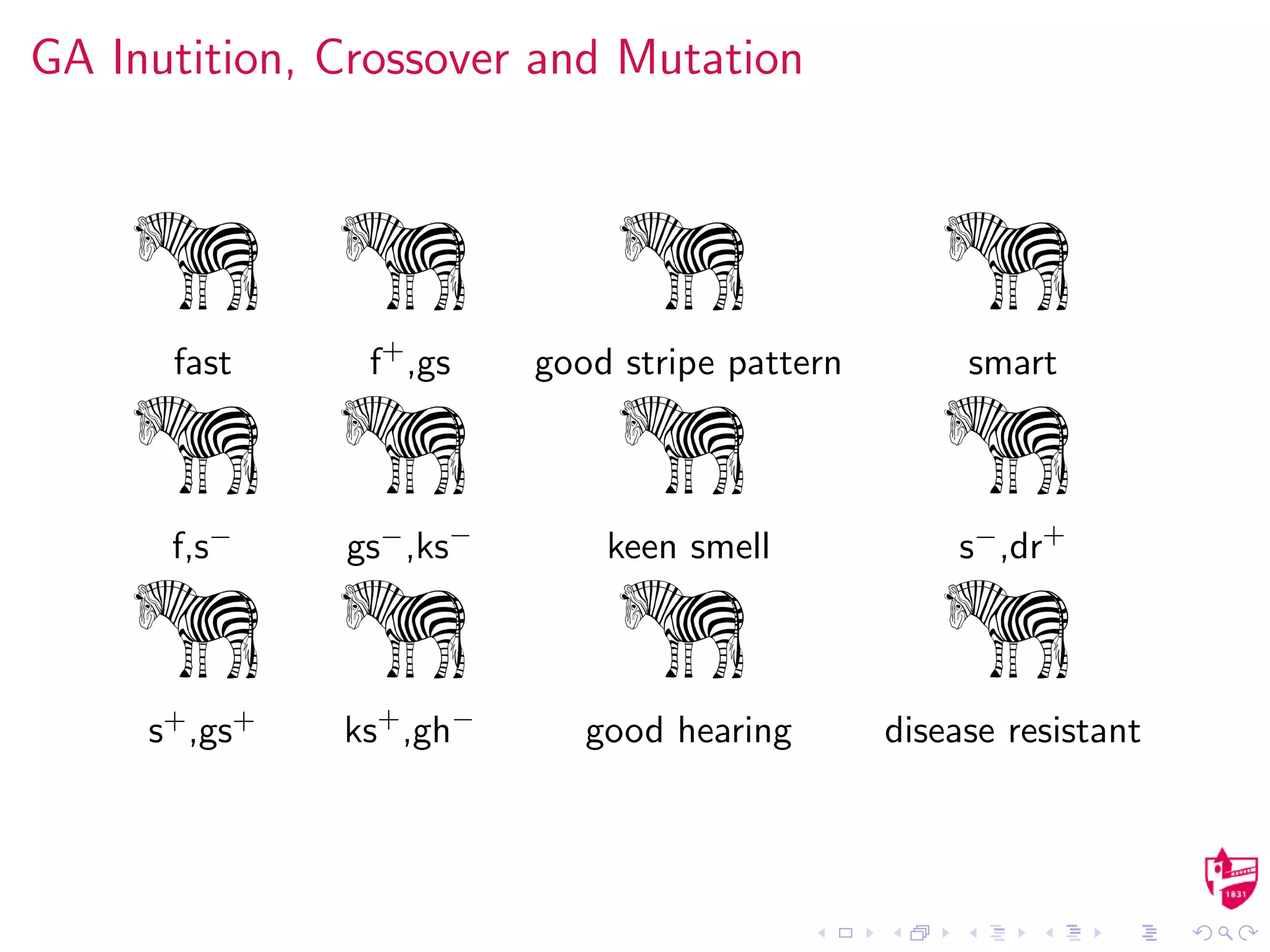
17. Stochastic Integer Search
We use a custom, integer-based genetic algorithm-esque search
that does the following:
We use random permutations of the integers in the set
{1, . . . , q} (q is the number of scheduling opportunities) to
create each member of the population. The population
P ∈ Zm×n[1, q] where n ≤ q.
In our formulation, mutation over the integers and crossover
were equivalent–a swap.

18. Fitness Functional
How do I determine a good solution may be?
Criteria:
1. Make sure I get a “solution” where the class fits in the space.
2. Can’t double-book a professor.
How do we do that?

19. Fitness Functional, Class Fits the Room
Randomly generate the population P and select the ith
member.
Corresponding to the population member, Pi we assign
R(Pi ) := C
where C is the list of the enrollment caps of our offered
courses (of length q) and R is the list of our “bins”.

20. Class Fits the Room, cont.
Define
S is the number of seats for classrooms at the designated
times.
The Heaviside function as
H(x) =
1 x > 0
0 x ≤ 0
Then, create a function
J1(Pi ) =
q
j=1
H (Rj (Pi ) − Sj ) .

21. Fitness Functional, Don’t Overbook the Professor
Corresponding to the population member, Pi we assign
A(Pi ) := T
where T is the list of the instructors of our offered courses
(of length q) and A is the list of our instructor “bins”.
Reshape the list A to look like a grid of rooms by time.
Aq×1 → ˜A(r×t)
where r is the number of rooms we can use and t is the
number of time slots.

22. Don’t Overbook the Professor, cont.
Now, I do a columnwise sort on ˜A.
˜As = sort ˜A .
To determine the number of overbookings, I do some Boolean
logic.
J2(Pi ) = ˜As ≡ 0 − unique ˜As ≡ 0

23. Optimization Problem
The optimization problem then becomes
min
Pi ∈Z1×q
J(Pi ) = min
Pi ∈Z1×q
(J1(Pi ) + J2(Pi ))
= min
Pi ∈Z1×q


q
j=1
H (Rj (Pi ) − Sj )
+ ˜As ≡ 0 − unique ˜As ≡ 0

24. Class Schedules
MWF TTh
8:30a-9:30a 8:00a-9:30a
9:40a-10:40a 9:40a-11:15a
10:50a-11:50a 1:00p-2:30p
12:30p-1:30p 2:40p-4:10p
1:40p-2:40p
2:50p-3:50p

25. Science Building
Removed all labs and spaces that require specialty scheduling.
Nine classrooms.
38 classes.
17 professors.
Results follow.

26. Size of the Scheduling Problem
383 individual courses (labs, recitals, etc.)
Covers hundreds of spaces on campus.
Of the spaces, many have specialty equipment and are not for
general use.
Some are computer labs.

27. Lesson One
If you cannot solve a problem, make it easier.

28. Reduced Problem
If we reduce our problem in this way, here’s what we do:
Remove all science and computer labs.
Remove any recital or performance spaces.
Remove any spaces with healthcare technology (nursing).
Remove any spaces with exercise/strength/conditioning
equipment.
Building Name Number of Classrooms
Callaway Academic 6 (14,16,30,30,30,40)
Smith Hall 7 (14,20,21,22,23,25,48)
Hawkes Hall 2 (24,24)
Manget 9 (12,12,12,14,14,20,24,24,24)
Callaway Science 9 (18,18,24,24,24,34,40,48,64)
Total 33

29. Lesson Two
Money solves lots of problems.

30. Campus Problem
180 courses
67 different professors
33 rooms
330 scheduling opportunities.

31. Campus Problem, Results
There are only flawed results.
So far, the best results I’ve found still have 9 scheduling errors.
Runtime is about 31 minutes.

32. Future Work
Prioritize classes to be in the same building as that of the
office of the professor.
Build in early morning and late afternoon bounds.
Experiment with Longer calendars.
Implement inter-departmental demands.

33. Some Additional Lessons
Mathematicians are problem solvers.
There is always low-hanging fruit to be plucked.
Failure is okay.
We just report the news; we don’t make it.

34. References I
J.H. Holland.
Genetic algorithms and the optimal allocation of trials.
SIAM Journal of Computing, 2(2), 1973.