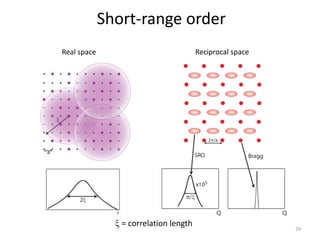
This document discusses the use of diffuse x-ray scattering to study short-range order and atomic displacements in alloys. Three key points: 1) Diffuse scattering patterns provide information about correlations between atoms over short lengths scales, revealing phenomena like chemical ordering, clustering, and thermal vibrations. 2) Experiments using synchrotron sources and advanced analysis allow direct comparison of diffuse scattering data to first-principles calculations, providing new insights into phase stability and properties like magnetostriction. 3) A study of Fe-Ga alloys found that slow cooling produces longer-range chemical ordering compared to quenching, and correlations depend strongly on composition, with anisotropic increases in correlation length influencing magnet

1. Displacement Short Range Order and the
Determination of Higher Order Correlation
Y. S. Puzyrev, D. M. Nicholson, R. I. Barabash, G. Stocks, G. Ice
Oak Ridge National Laboratory
R. McQueeney
Ames National Laboratory
Yingzhou Du
Iowa State University

2. Outline
• Short Range Order and Diffuse Scattering
• Experimental Method
• Data Analysis and Atomic Structure
• Pair and Many-body Correlations
• Displacement SRO and Higher Order Correlations in
One-dimensional Model
• First Principles Calculation of Atomic Displacement in
Fe46.5 Ni53.5 Fe80.0Ga20.0

3. Diffuse scattering poised for a revolution!
• Synchrotron sources /new tools enable new
applications
– Rapid measurements for combinatorial
and dynamics
– High energy for simplified data analysis
– Small (dangerous) samples
• Advanced neutron instruments emerging
– Low Z elements
– Magnetic scattering
– Different contrast
• New theories provide direct link beween
experiments and first-principles calculations
Experiment Theory
Major controversies have split leading scientists in once staid community!

4. Diffuse scattering due to local (short ranged)
correlations/ fluctuations
• Thermal diffuse scattering (TDS)
• Point defect
– Site substitution
– Vacancy
– Interstitial
• Precipitate
• Dislocations
• Truncated surface- more
All have in common reduced correlation length!

5. Bragg reflection occurs when scattering amplitudes
add constructively
• Orientation of sample
• Wavelength
• Bragg Peaks sharp! ~1/N
(arc seconds)
h ˆ
Think in terms of momentum transfer p0 = d0
l

6. Length scales are inverted!
• Big real small reciprocal
• Small real big reciprocal
• We will see same effect in
correlation length scales
– Long real-space correlation
lengths scattering close to
Bragg peaks
If you remember nothing else!

7. Krivoglaz classified defects by effect on Bragg Peak
Intensity
• Defects of 1st kind No defects
– Bragg width unchanged
– Bragg intensity decreased
– Diffuse redistributed in reciprocal space
– Displacements remain finite Defects of 1st kind
• Defects of 2nd kind
– No longer distinct Bragg peaks
Defects of 2nd kind
– Displacements continue to grow with
crystal size

8. Thermal motion-Temperature Diffuse Scattering-
(TDS) -defect of 1st kind
• Atoms coupled through atomic
bonding
• Uncorrelated displacements at
distant sites
– (finite)
• Phonons (wave description)
– Amplitude
– Period
– Propagation direction
– Polarization
(transverse/compressional)
Sophisticated theories from
James, Born Von Karmen, Krivoglaz

9. A little math helps for party conversation
• Decrease in Bragg intensity
scales like e-2M, where
sin2 q
2M = 16p u2 2
s
l
Low Temperature
• Small Big reflections
• e-2M shrinks (bigger effect)
with (q)
High temperature
Displacements, us depend on Debye Temperature D –
Bigger D smaller displacements !

10. TDS makes beautiful patterns reciprocal space
sodium Rock salt
• Iso- intensity contours
– Butterfly
– Ovoid
– Star
• Transmission images
reflect symmetry of Experiment Theory
reciprocal space and
TDS patterns
Chiang et al. Phys. Rev. Lett.
83 3317 (1999)

11. Often TDS mixed with additional diffuse scattering
• Experiment
• Strain contribution
• Combined
theoretical TDS and
strain diffuse
scattering
TDS must often be removed to reveal other diffuse scattering

12. Alloys can have another type 1
defect-site substitution
Each Au has 8 Cu near-neighbors
• Long range
– Ordering (unlike neighbors)
Cu3Au
– Phase separation (like
neighbors) L12
• Short ranged
– Ordering
CuAu
– Clustering (like neighbors)
L10
Alternating planes of Au and Cu

13. Redistribution depends on kind of correlation
Clustering intensity
fundamental sites
Random causes
Laue monotonic
Short-range ordering
superstructure sites

14. Neutron/ X-rays Complimentary For
Short-range Order Measurements
• Chemical order diffuse scattering
proportional to contrast (fA-fB)2
• Neutron scattering cross sections
– Vary wildly with isotope
– Can have + and – sign
– Low Z , high Z comparable
• X-ray scattering cross section
– Monotonic like Z2
– Alter by anomalous scattering

15. Neutrons can select isotope to
eliminate Bragg scattering
• Total scattering cafa2+ cbfb2 = 3 +1 +1 +1
-3 +1
+1 +1 -3
• Bragg scattering (cafa+ cbfb = 0
)2 +1 +1 +1
-3 +1
• Laue (diffuse) scattering +1 +1 -3 0 0
0
cacb(fa- -fb)2 =3 0 0
0 0 0
Isotopic purity important as different isotopes have distinct
scattering cross sections- only one experiment ever done!

16. X-ray anomalous scattering can change x-ray contrast
• Chemical SRO scattering scales like (fa-fb)2
• Static displacements scale like (fa-fb)
• TDS scales like ~faverage2

17. Atomic size (static displacements) affect phase stability/
properties
• Ionic materials (Goldschmidt)
– Ratio of Components
– Ratio of radii
– Influence of polarization
FeFe
r 110
• Metals and alloy phases (Hume-Rothery) c
– Ratio of radii r FeNi
110
– Valence electron concentration
– Electrochemical factor NiNi
r 110 a
a
Grand challenge -include deviations from lattice in modeling of alloys

18. Measurement and theory of atomic size are hard!
• Theory- violates repeat lattice
approximation- every unit cell
different!
• Experiment
– EXAFS marginal (0.02 nm) in
dilute samples
– Long-ranged samples have
balanced forces
Important!

19. Systematic study of bond distances in Fe-Ni alloys
raises interesting questions
• Why is the Fe-Fe bond
distance stable?
• Why does Ni-Ni bond
swell with Fe
concentration?
• Are second near neighbor
bond distances
determined by first
neighbor bonding?

20. Diffuse x-ray scattering measurements of AgPd alloy finds
surprising lack of local ordering
• Negative deviation from Vegard’s
law indicates ordering.
• First principle theory predicts
ordering.- Good system for theory.
• Semi-empirical theory predicts
clustering.

21. High-energy x-ray measurements revolutionize
studies of phase stability
• Data in seconds instead
of days
• Minimum absorption
and stability corrections
• New analysis provides
Crystal growth
direct link to first-
principle Experimental
measurement of short
range structures
Max Planck integrates diffuse x- Data analysis
ray scattering elements! Rapid measurement
ESRF

22. Measurements show competing tendencies to order
Au3Ni -001 plane
• Both L12 and Z1 present
• Compare with first
principles calculations
Reichert et al. Phys. Rev. Lett. 95 235703 (2005)

23. New directions in diffuse scattering
• Microdiffuse x-ray scattering
– Combinatorial
– Easy sample preparation
• Diffuse neutron data from
every sample
• Interpretation more closely
tied to theory
– Modeling of scattering x-
ray/neutron intensity
Experiment Model

24. Intense synchrotron/neutron sources realize the promise
envisioned by pioneers of diffuse x-ray scattering
• M. Born and T. Von Karman 1912-1946- TDS
• Andre Guiner (30’s-40’s)-qualitative size
• I. M. Lifshitz J. Exp. Theoret. Phys. (USSR) 8 959
(1937)
• K. Huang Proc. Roy. Soc. 190A 102 (1947)-long
ranged strain fields
• J. M Cowley (1950) J. Appl. Phys.-local atomic
size
• Warren, Averbach and Roberts J. App. Phys 22
1493 (1954) -SRO
• Krivoglaz JETP 34 139 1958 chemical and spatial
fluctuations
Other references:
• X-ray Diffraction- B.E. Warren Dover Publications New York 1990.
• http://www.uni-wuerzburg.de/mineralogie/crystal/teaching/dif_a.html
• Krivoglaz vol. I and Vol II.

25. Diffuse scattering done by real people-small community
S. Cowley, Arizona St.
• Warren school
Bernie Borie,ORNL Cullie Sparks
ORNL
Jerry Cohen, Northwestern
B. Schoenfeld, ETH Zurich
A. Gunier W. Schweika, KFA Jülich
Simon Moss,U. Of Houston
• Krivoglaz school
Peisl, U. München
Gitgarts,Minsk Rosa Barabash
IMP, ORNL Gene Ice
Rya Boshupka, IMP ORNL

26. Advanced Photon Source
Argonne National Laboratory, Chicago IL

27. Upcomingin 2015: NSLS 2 in Brookhaven

28. Diffuse Scattering
2
 *
  
k rp rq
 
I total k fp f e
q I Bragg k I diffuse k
p ,q
f p - atomic scattering factor of atom p
   
I diffuse k I SRO k I static k ITDS k
Real Space Reciprocal Space

29. Short-range order
Real space Reciprocal space
= correlation length
29

30. Short-range atomic ordering in Galfenol
• Position of doped Ga atoms influences
magnetostriction
– Quenched material has larger MS
– MS is suppressed in D03 ordered samples
– Proposed that uniaxial Ga pairing enhances MS
(R. Wu, JAP 91, 7358, 2002)
• Ga atom distributions measured using X-ray
scattering
– Long-range order (Ga ordering, D03, B2, L12)
– Short-range order (Ga clustering, pairing)
• Can study variation of Ga clustering with …
– Sample composition
– Heat treatment
– Temperature
– Stress/strain state
– Magnetic field 30

31. Fe-Ga structures and
reflection conditions
Reflection A2 (BCC) B2 (SC) D03 (FCC)
(1,0,0) X  
(2,0,0)   
(1,1,0)   
(1,1,1) X  
(1/2,1/2,1/2) X X 
(1/2,1/2,0) X X X
31

32. Experimental Method
• Measurements performed at UNI-CAT
(Sector 33ID-D APS)
– Absorption edge energy monochromatic x-rays
• (E=7.1 and 10.32 keV)
– Measure weak diffuse scattering signal
– Point detector for quantitative data
• Sample Fe80Ga20
– Crystals prepared at Ames Lab by Bridgman technique
– Samples cut Size ~ 5x5x0.5 mm
– “Quenched” - rapidly cooled
– Etched for x-ray scattering

33. Data
100000
(100) 26% quenched (111)
LRO
10000
Counts/monitor
1000 18.7% slow-cooled
SRO
100
10
1
0.1
-0.5 0.0 0.5 1.0 1.5 2.0
[1,L,L]
Thermal diffuse Short-range
scattering order
Thermal diffuse Short-range order
33

34. Conversion of the Data to Electron Units
• Scattering factors, - corrected for x-ray absorption fine structure (XAFS) and
Lorentzian hole width of an inner shell.
• Compton and Resonant Raman inelastic scattering is separated and removed from
integrated intensities.
•Ni standard integrated intensities are obtained to compute conversion factor.

35. Short-Range Order Parameters
Anomalous (resonant) scattering
Warren-Cowley Short-Range Order Parameters
AB
Plmn AB
lmn 1 , where Plmn probability to find atom Ain shell ' lmn ' away from B
cA

36. Large Scattering Factor Contrast
12 eV below Fe absorption edge
E = 7.100 keV
Small Scattering Factor Contrast
50 eV below Ga absorption edge
E = 10.320 keV

37. Large atomic displacements are instrumental for
understanding of occurrence of DO3 phase

38. Magnetistriction Effect
Experiment at high energy E= 80-120 keV, R. McQueeney
• Correlation lengths 1.00 1.0
Fe100-xGax 1.1
– Slow-cooled more ordered than 0.75 1.3
1.6
quenched 0.50 2.0
2.7
– At low x, ~ 2-4 unit cells 0.25 4.0
SRO Peak Width (Units of 2 /a)
8.0
•
(1/2,1/2,1/2) (3/2,1/2,1/2)
Correlation Length (Unit Cells)
Slow-cooled 0.00
1.1
– dramatic increase in correlation length
(100)SC
(100)Q
0.75 (011)SC
1.3
(011)Q
1.6
above 17.7% 0.50
(111)SC
(111)Q
2.0
•
2.7
Quenched 0.25 4.0
(100) (3/2,3/2,3/2) 8.0
– Gradual increase in correlation length 0.00
1.1
• Anisotropy 0.75 1.3
1.6
– Long correlation lengths along (111) 0.50 2.0
2.7
– Anisotropy disappears at high Ga% 0.25 4.0
(111) (5/2,1/2,1/2) 8.0
0.00
12 13 14 15 16 17 18 19 20 13 14 15 16 17 18 19 20
x, Ga Composition (%)
• Atomic displacements – increase
before magnetostriction decreases

39. X-ray diffraction diffuse scattering experiment
Warren-Cowley SRO parameters
Atomic displacements lmn lmn
where lmn include 20 or more shells
Based on this information one can reconstruct
atomic configuration
If interactions are accurately described by
Pair Hamiltonian, the higher order correlations
are reproduced correctly from pair correlations
which can be shown using DFT
Classical DFT: R. Evans, Advances in Physics 28, 2, 143 (1979)

40. Test multi-atom real-space correlations in Reverse Monte-
Carlo model against equilibrium configurations
Create equilibrium configurations
With realistic interactions
• Set 1 - pair interactions
to 4th neighbor
Determine pair and higher
• Set 2 -pair +multi-atom Order correlations
interactions
Construct a configuration
By Reverse Monte-Carlo
From pair correlations
Compare
Determine pair and higher correlations
Order correlations

41. Nearest Neighbor distribution
• Pair correlations determine all higher order correlations
•Equilibrium for pair potential Hamiltonians.
•Constructed • For many body Hamiltonians they do not.
•Random • Derivatives provide information about higher order
correlations: pressure, magnetic field, stress,…

42. SRO in 1D Model with PBC
•Show that displacements SRO limits higher order correlations
•Simple analytical model
Iso- g (r ) process used to check realizability of
pair correlation function
Inappropriateness of so called “reverse Monte Carlo
Method” that uses a candidate pair correlation function
as a means to suggest typical many-body configuraitons
F. H. Stillinger,S. Torquato, “Pair Correlation Function Realizability”, J. Phys. Chem. B 108, 19589

43. Lattice Model
n, N configuration of n particles distributed on N sites
For example
Class collects all members that differ only by
•Translation
•Inversion j
m j number of configurations
N 11
w j weight
n 3

44. Enumeration of states
Given
The weights have to be positive g (r )
The solution of linear equations
1 2 2w1 2w2 2w3 k • Exists and not unique
•1,2, n dimensional manifold
1 3 2w2 2w4 w5 k
w1 2w3 2w5 k • Exists and unique
1 4
etc... • Doesn’t exist

45. Displacements SRO in 1D Model with PBC
• Suppose that there is an average ‘lattice’ and
introduce displacements off the ideal positions
• Create a simple RULE for the displacement
dependence on chemical environment
Displacement table
101 N
Displace 0 in the
001 R
1 middle to the right if 100 L
j , j
0 is to the left and 1 111 N
0
is to the right 011 L
0
110 R
000 N

46. Displacements SRO in 1D Model with PBC
d1d4 = w1 + w3 + 2w5 = f This puts additional restrictions
On the possible configurations
etc...
s 1s 2 = 2w1 + 2w2 + 2w3 = k The displacements in the real
system must give an indication
s 1s 3 = 2w2 + 2w4 + w5 = k whether the particular local
environment is realizable or not,
s 1s 4 = w1 + 2w3 + 2w5 = k i.e. restrict the higher order
correlations in the system
etc...

47. Average correlations: point, pair, triplet
1 A
i
1 B
N
1 2c 1
N i 1
i
N
2
1 4(c 2 c 1 c ) 2c 1
j N i i j j
i 1
 ö-1
N
 æ V (q)
a ( q ) = ç1+ 2cA cB ÷
3
1
j ,k N i i j i k
i 1
è kB T ø

48. Real alloy system
Fe46.5 Ni53.5
N
2
1 Configurations with the same pair correlations
j N i 1
i i j
Vary triplet correlations
1-st
Compute displacements from first principles
Compare the displacements with
Measured values

49. Configurations with triplet correlation variation
P AAA
11 0.1 A Ni P AAA
11 0.4
Reverse
Monte-Carlo
128 atom
VASP
Displacements
Experiment
Fe 4.09e-4 Ni 1.70e-4 Fe 0.028 Ni 0.012 Fe 7.09e-4 Ni 0.70e-4

50. Conclusion
• One-dimensional model shows that displacement SRO
further restricts higher order correlations
• For realistic system calculation of displacements can
give qualitative prediction of higher order
correlations.