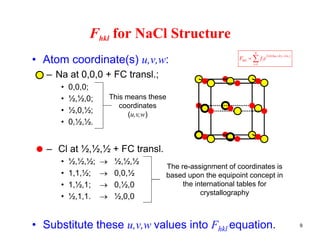
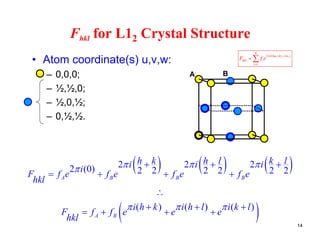
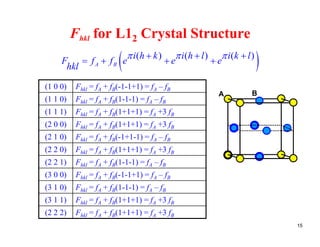
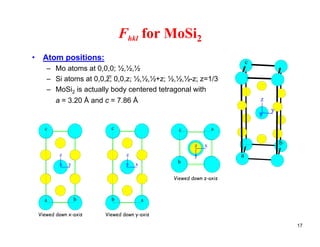
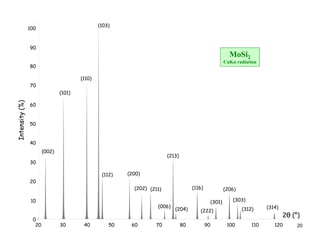
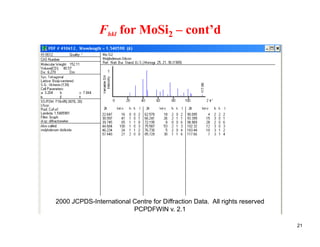
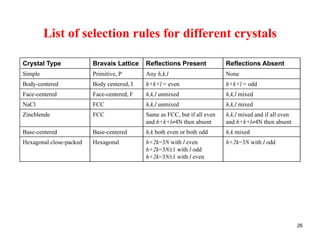
The structure factor (Fhkl) describes how the atomic arrangement influences the intensity of scattered x-rays in diffraction patterns. It is calculated as the sum of all atomic scattering factors multiplied by their positions. Fhkl tells us which diffraction peaks (hkl reflections) will be present. Different crystal structures have characteristic Fhkl equations and diffraction patterns depending on their atomic positions. Examples include simple cubic, body centered cubic, face centered cubic, NaCl, L12, and MoSi2 structures.

1. The Structure FactorThe Structure Factor
Suggested Reading
P 303 312 i D G f & M HPages 303-312 in DeGraef & McHenry
Pages 59-61 in Engler and Randle
1

2. Structure Factor (Fhkl)
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
• Describes how atomic arrangement (uvw)
1i
influences the intensity of the scattered beam.
It tells us which reflections (i e peaks hkl) to• It tells us which reflections (i.e., peaks, hkl) to
expect in a diffraction pattern.
2

3. Structure Factor (Fhkl)
• The amplitude of the resultant wave is given by a
ratio of amplitudes:ratio of amplitudes:
amplitude of the wave scattered by all atoms of a UC
li d f h d b l
hklF 
• The intensity of the diffracted wave is proportional
amplitude of the wave scattered by one electron
hkl
• The intensity of the diffracted wave is proportional
to |Fhkl|2.
3

4. Some Useful Relations
ei = e3i = e5i = … = -1
e2i = e4i = e6i = … = +1
eni = (-1)n, where n is any integery g
eni = e-ni, where n is any integer
eix + e-ix =2 cos x
Needed for structure factor calculationsNeeded for structure factor calculations
4

5. Fhkl for Simple Cubic
• Atom coordinate(s) u,v,w:
– 0,0,0
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
0,0,0
2 (0 0 0 )i h k l2 (0 0 0 )i h k l
hklF fe f     
 
No matter what atom coordinates or plane indices you substitute into theNo matter what atom coordinates or plane indices you substitute into the
structure factor equation for simple cubic crystals, the solution is always
non-zero.
5
Thus, all reflections are allowed for simple cubic (primitive) structures.

6. Fhkl for Body Centered Cubic
• Atom coordinate(s) u,v,w:
– 0,0,0;
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
0,0,0;
– ½, ½, ½.
2
h k l
i
 
 2
2 (0) 2 2 2
h k l
i
i
hklF fe fe


 
  
 
 

 
 1 i h k l
F f e
hkl
  
 
When h+k+l is even Fhkl = non-zero → reflection.
6
When h+k+l is odd Fhkl = 0 → no reflection.

7. Fhkl for Face Centered Cubic
• Atom coordinate(s) u,v,w:
– 0,0,0;
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
0,0,0;
– ½,½,0;
– ½,0,½;
– 0,½,½.
 
2 2 2
2 0 2 2 2 2 2 2
h k h l k l
i i i
i
f f f f
  

            
      2 0 2 2 2 2 2 2i
hklF fe fe fe fe      
   

7
     
 1 i h k i h l i k l
hklF f e e e    
   

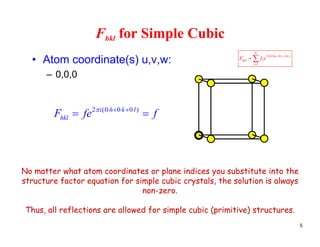
8. Fhkl for Face Centered Cubic
     
 1 i h k i h l i k l
hklF f e e e    
   
• Substitute in a few values of hkl and you will find
the following:the following:
– When h,k,l are unmixed (i.e. all even or all odd), then
Fhkl = 4f. [NOTE: zero is considered even]
F 0 f i d i di (i bi ti f dd– Fhkl = 0 for mixed indices (i.e., a combination of odd
and even).
8

9. Fhkl for NaCl Structure
• Atom coordinate(s) u,v,w:
– Na at 0,0,0 + FC transl.;
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
Na at 0,0,0 FC transl.;
• 0,0,0;
• ½,½,0;
½ 0 ½
This means these
coordinates
• ½,0,½;
• 0,½,½.
coordinates
(u,v,w)
– Cl at ½,½,½ + FC transl.
• ½,½,½;  ½,½,½
1 1 ½ 0 0 ½
The re-assignment of coordinates is
• 1,1,½;  0,0,½
• 1,½,1;  0,½,0
• ½,1,1.  ½,0,0
g
based upon the equipoint concept in
the international tables for
crystallography
9• Substitute these u,v,w values into Fhkl equation.

10. Fhkl for NaCl Structure – cont’d
• For Na:
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
 2 (0) ( ) ( ) ( )i i h k i h l i k l
f e e e e     
    
 
( ) ( ) ( ) ( )
( ) ( ) ( )
1
Na
i h k i h l i k l
Na
f e e e e
f e e e    
   
  
• For Cl:
 
 
2 ( ) 2 ( ) 2 ( )( ) 2 2 2
l k hi h k i h l i k li h k l
Clf e e e e
         
   
 
 
( ) ( ) ( ) ( )
( ) ( ) ( )
2 2 2 2
( )
2 2i h k l i i ih k h l k l
Cl
i h k l i i i
Cl
f e e e e
f e e e e
   
   
       
 
   
  
l k h
l k h
These terms are all positive and even.
 Whether the exponent is odd or
10
 Whether the exponent is odd or
even depends solely on the remaining
h, k, and l in each exponent.

11. Fhkl for NaCl Structure – cont’d
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 • Therefore Fhkl:
 
 
( ) ( ) ( )
( ) ( ) ( ) ( )
1 i h k i h l i k l
hkl Na
i h k l i i i
Cl
F f e e e
f e e e e
  
   
  
 
    
  l k h
 Clf e e e e  
which can be simplified to*:
  ( ) ( ) ( ) ( )
1i h k l i h k i h l i k l
hkl Na ClF f f e e e e       
    
11

12. Fhkl for NaCl Structure
When hkl are even Fhkl = 4(fNa + fCl)
Primary reflectionsPrimary reflections
When hkl are odd F = 4(f f )When hkl are odd Fhkl = 4(fNa - fCl)
Superlattice reflections
When hkl are mixed Fhkl = 0
N fl tiNo reflections
12

13. (200)
100
80
90
NaCl
CuKα radiation
(220)
%)
60
70
Intensity(
50
I
30
40
(111)
(222)
(400)
(420)
(422) (600)
(442)
10
20
13
(111)
(311)
(400)
(331)
(333)
(511)
(440)
(531)
20 30 40 50 60 70 80 90 100 110 120
2θ (°)
0
10

14. Fhkl for L12 Crystal Structure
• Atom coordinate(s) u,v,w:
– 0,0,0; A B
2 ( )
1
i j i
N
i hu kv lw
hkl i
i
F f e
  

 
0,0,0;
– ½,½,0;
– ½,0,½;
A
– 0,½,½.
     2 2 22 (0) 2 2 2 2 2 2
h k h l k li i ii           2 (0) 2 2 2 2 2 2
A B B B
i
F f e f e f e f e
hkl
   

14
 ( ) ( ) ( )
A B
i h k i h l i k l
F f f e e e
hkl
    
   

15. Fhkl for L12 Crystal Structure
 ( ) ( ) ( )
A B
i h k i h l i k l
F f f e e e
hkl
    
   
(1 0 0) Fhkl = fA + fB(-1-1+1) = fA – fB
(1 1 0) Fhkl = fA + fB(1-1-1) = fA – fB
A B
(1 1 1) Fhkl = fA + fB(1+1+1) = fA +3 fB
(2 0 0) Fhkl = fA + fB(1+1+1) = fA +3 fB
(2 1 0) Fhkl = fA + fB(-1+1-1) = fA – fB(2 1 0) Fhkl fA fB( 1 1 1) fA fB
(2 2 0) Fhkl = fA + fB(1+1+1) = fA +3 fB
(2 2 1) Fhkl = fA + fB(1-1-1) = fA – fB
(3 0 0) Fhkl = fA + fB(-1-1+1) = fA – fB
(3 1 0) Fhkl = fA + fB(1-1-1) = fA – fB
(3 1 1) Fhkl = fA + fB(1+1+1) = fA +3 fB
15
(3 1 1) Fhkl fA + fB(1+1+1) fA +3 fB
(2 2 2) Fhkl = fA + fB(1+1+1) = fA +3 fB

16. Intensity (%)
100
(111)
Example of XRD pattern
from a material with an
L12 crystal structure
A B
80
90
100
A B
60
70
80
40
50
60
(200)
30
40
(220)
(311)
2 θ (°)
10
20
(100)
(110)
(210) (211) (221)
(300)
(310)
(222)
(320) (321)
16
( )
20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115
0
( ) ( )

17. Fhkl for MoSi2
• Atom positions:
– Mo atoms at 0,0,0; ½,½,½
Si t t 0 0 0 0 ½ ½ ½ ½ ½ ½ 1/3
c
– Si atoms at 0,0,z; 0,0,z; ½,½,½+z; ½,½,½-z; z=1/3
– MoSi2 is actually body centered tetragonal with
a = 3.20 Å and c = 7.86 Å z
c c ac
x
y
x y
z
xy
z
b
x
y
z
a
b
a b ab
Viewed down z-axis
17
a a
Viewed down x-axis Viewed down y-axis

18. Fhkl for MoSi2
Substitute in atom positions:
( )2
1
  

  i j i
N
i hu kv lw
hkl i
i
F f e
• Mo atoms at 0,0,0; ½,½,½
• Si atoms at 0,0, ; 0,0,z; ½,½,½+z; ½,½,½-z; z=1/3
     5   h k l h k l h k ll l
     
   
52 2 22 ( ) 2 ( )2 (0) 2 2 2 2 2 6 2 2 63 3
5
   
           
        
   
   
 
h k l h k l h k ll li i ii ii
F f e f e f e f e f e f e
hkl Mo Mo Si Si Si Si
l ll l h k h k     52 ( ) 2 ( )
3 33 31
  
        
        
   
 
l ll l i h k i h ki ii h k l
F f e f e e e e
Mo Si
Now we can plug in different values for h k l to determine the structure factor.
F h k l 1 0 0• For h k l = 1 0 0
 
     5(0) (0)(0) (0)
3 33 3
1 0 1 02 ( ) 2 ( )1 0 0
2
1
0
(1 1) (1 1 1 1) 0
               
  
      
i ii ii
hkl Mo Si
hkl
Mo Si
F f e f e e e e
F
f f
18
2
( ) ( )
You will soon learn that intensity is proportional to ; there is NO REFLECTION!
Mo S
l
i
hkF
f f

19. Now we can plug in different values for h k l to determine the structure factor
Fhkl for MoSi2 – cont’d
Now we can plug in different values for h k l to determine the structure factor.
• For h k l = 0 0 1
 
     5(1) (1)
1 1
3 33 3
0 0 0 02 ( ) 2 ( )0 0 10                
 
i ii ii
hkl Mo SiF f e e f e e e e
22
3(1 ) (2 ( ) )
(1 1) ( 1 1) 0
 
   
     

i i
Mo Si
Mo si
f e f COS e
f f
• For h k l = 1 1 0
2
0 NO REFLECTION!hklF
 
     
 1 1 0 1 1 0 1 1 00 2 (0) 2 (0)
2 (0) (0) 2 2
(1 ) ( )
(2) (4)
   
  
     
     
     
 
i i ii i
hkl Mo Si
i i i
Mo Si
Mo si
F f e e f e e e e
f e f e e e e
f f
If you continue for different h k l combinations trends will emerge this will lead you
2
POSITIVE! YOU WILL SEE A REFLECTION

hklF
19
• If you continue for different h k l combinations… trends will emerge… this will lead you
to the rules for diffraction…
h + k + l = even

20. 100
(103)
80
90
(110)
MoSi2
CuKα radiation
%)
60
70
(101)
(110)
Intensity(
50
I
30
40
(002)
(213)
10
20
(112) (200)
(202) (211) (116)
(301)
(206)
(303)
2020 30 40 50 60 70 80 90 100 110 120
2θ (°)
0
10
(006)
(204) (222)
(301) (303)
(312) (314)

21. Fhkl for MoSi2 – cont’d
2000 JCPDS International Centre for Diffraction Data All rights reserved
21
2000 JCPDS-International Centre for Diffraction Data. All rights reserved
PCPDFWIN v. 2.1

22. Structure Factor (Fhkl) for HCP
2 ( )i j i
N
i hu kv lw
F f
  

• Describes how atomic arrangement (uvw)
( )
1
i j i
hkl i
i
F f e

 
• Describes how atomic arrangement (uvw)
influences the intensity of the scattered beam.
i.e.,
• It tells us which reflections (i.e., peaks, hkl) to
expect in a diffraction pattern from a given crystal
structure with atoms located at positions u v w
22
structure with atoms located at positions u,v,w.

23. • In HCP crystals (like Ru Zn Ti and Mg) the• In HCP crystals (like Ru, Zn, Ti, and Mg) the
lattice point coordinates are:
– 0 0 0
–
1 2 1
3 3 2
• Therefore, the structure factor becomes:
2
2
h k l
i  
   2
3 3 2
1
i
hkl iF f e
  
  
 
 
  
 

24. • We simplify this expression by letting:p y p y g
2 1
3 2
h k
g

 
which reduces the structure factor to:
 2
1 ig
hkl iF f e 
 
• We can simplify this once more using:
 1hkl iF f e
from which we find:
2ix ix
2cosix ix
e e x 
2 2 2 2
4 cos
h k l
F f 
   4 cos
3 2
hkl iF f   
 

25. Selection rules for HCP
0 when 2 3 and oddh k n l  
2
2
2
when 2 3 1 and even
3 when 2 3 1 and odd
i
hkl
f h k n l
F
f h k n l

    
 
   
2
3 when 2 3 1 and odd
4 when 2 3 and even
i
i
f h k n l
f h k n l
 
   
 For your HW problem, you will need these things to
do the structure factor calculation for Ru.
 HINT: It might save you some time if you already
had the ICDD card for Ru.ad t e C ca d o u

26. List of selection rules for different crystals
Crystal Type Bravais Lattice Reflections Present Reflections Absent
Simple Primitive, P Any h,k,l Nonep , y
Body-centered Body centered, I h+k+l = even h+k+l = odd
Face-centered Face-centered, F h,k,l unmixed h,k,l mixed
NaCl FCC h,k,l unmixed h,k,l mixed
Zincblende FCC Same as FCC, but if all even
and h+k+l4N then absent
h,k,l mixed and if all even
and h+k+l4N then absent
Base-centered Base-centered h,k both even or both odd h,k mixed
Hexagonal close-packed Hexagonal h+2k=3N with l even
h+2k=3N1 with l odd
h+2k=3N1 with l even
h+2k=3N with l odd
26

27. What about solid solution alloys?
• If the alloys lack long range order, then youIf the alloys lack long range order, then you
must average the atomic scattering factor.
falloy =xAfA + xBfB
where xn is an atomic fraction for the atomic
iconstituent
27

28. Exercises
• For CaF2 calculate the structure factor and
determine the selection rules for alloweddetermine the selection rules for allowed
reflections.
28