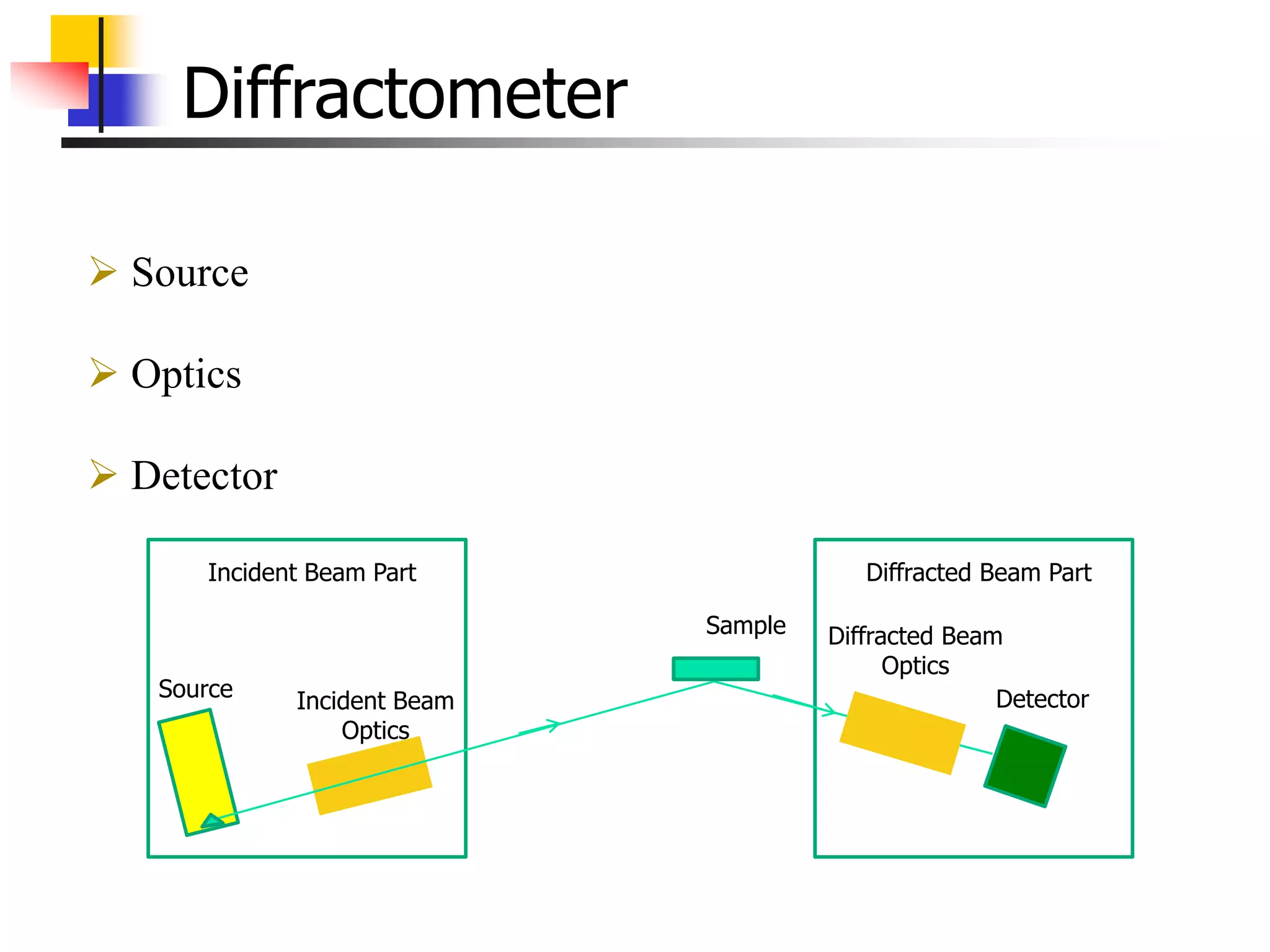
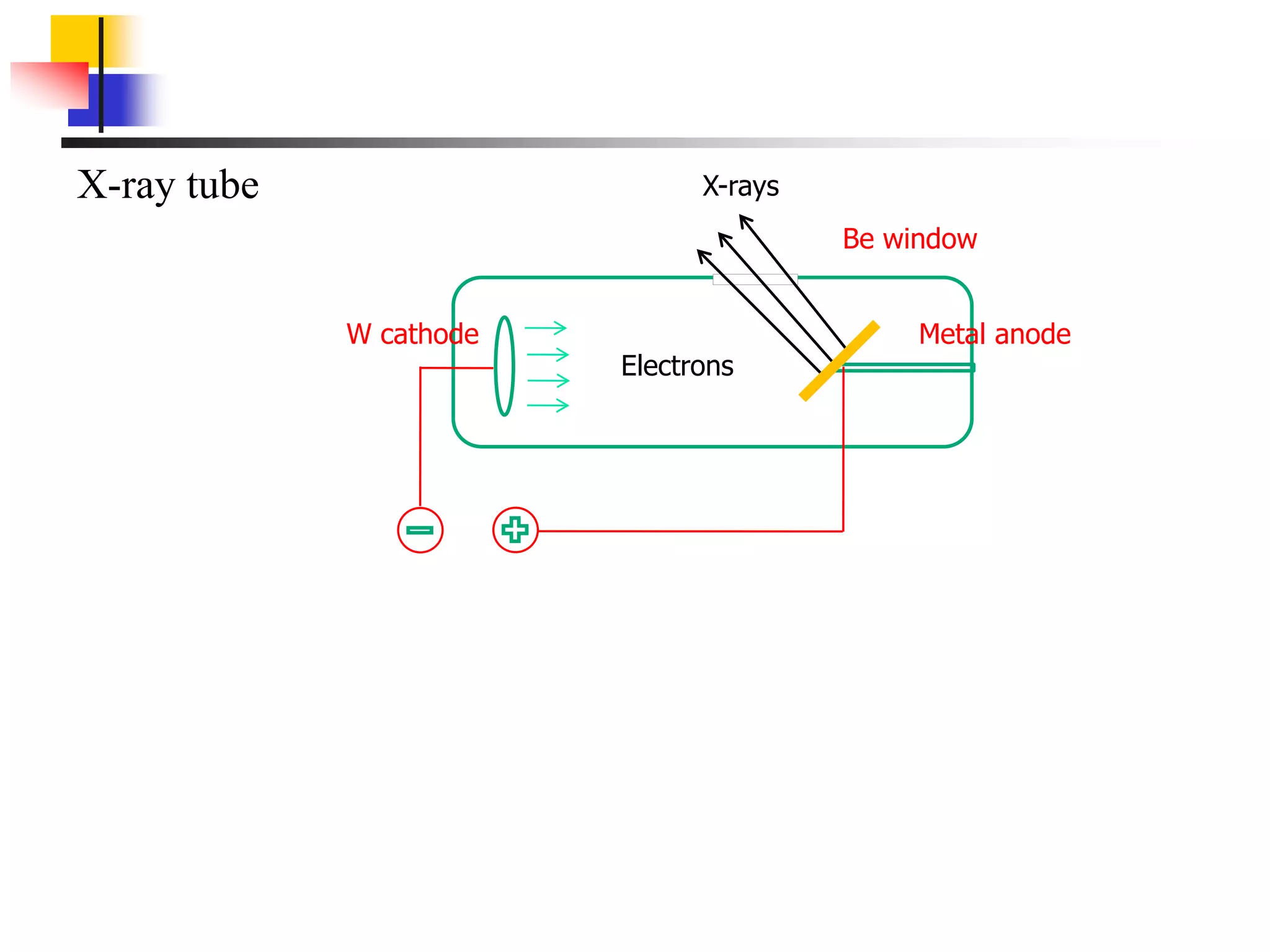
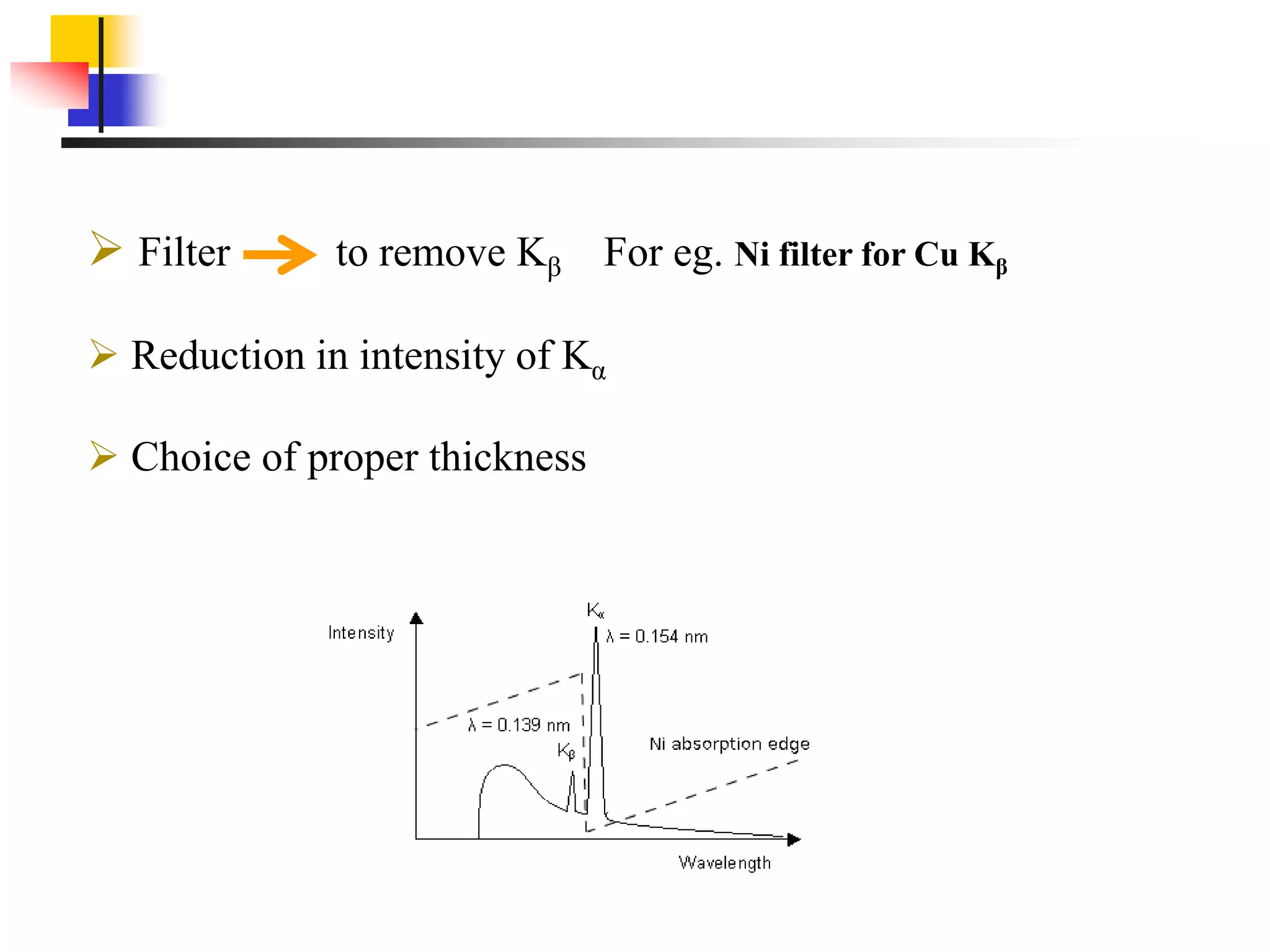
This document provides an overview of x-ray diffraction principles and practices. It begins with an introduction to materials characterization and the importance of x-ray diffraction. It then covers the basics of diffraction and Bragg's law. The document discusses different x-ray diffraction methods and techniques for analyzing crystal structure, phase, texture, stress, and particle size. It provides examples of analyzing diffraction patterns from single and multiple phases. Finally, it touches on concepts like broadening, texture, and pole figures.

1. X-ray Diffraction: Principles and Practice
Khan Hassnain Abbas

2. Layout of the Lecture
 Materials Characterization
 Importance of X-ray Diffraction
 Basics
 Diffraction
 X-ray Diffraction
 Crystal Structure and X-ray Diffraction
 Different Methods
 Phase Analysis
 Texture Analysis
 Stress Analysis
 Particles Size Analysis
 ………..
 Summary

3. Materials Characterization
 Essentially to evaluate the structure and
properties
 Structural Characterization
 Diffraction
 X-ray and Electron Diffraction
 Microscopy
 Spectroscopy
 Property Evaluation
 Mechanical
 Electrical
 Anything else

4. Time Line
 1665: Diffraction effects observed by Italian
mathematician Francesco Maria Grimaldi
 1868: X-rays Discovered by German Scientist
Röntgen
 1912: Discovery of X-ray Diffraction by
Crystals: von Laue
 1912: Bragg’s Discovery

5. Generation of X-rays

6. Crystal Systems and Bravais Lattices

7. Structure of Common Materials
 Metals
 Copper: FCC
 -Iron: BCC
 Zinc: HCP
 Silver: FCC
 Aluminium: FCC
 Ceramics
 SiC: Diamond Cubic
 Al2O3: Hexagonal
 MgO: NaCl type

8. Diffraction
 A diffracted beam may be defined as a beam
composed of a large number of scattered rays
mutually reinforcing each other
Scattering
Interaction with a single particle
Diffraction
Interaction with a crystal

9. Scattering Modes
 Random arrangement of atoms in space gives rise
to scattering in all directions: weak effect and
intensities add
 By atoms arranged periodically in space
 In a few specific directions satisfying Bragg’s law: strong
intensities of the scattered beam :Diffraction
 No scattering along directions not satisfying Bragg’s law

10. d
Diffraction of light through an aperture
-15 -10 -5 0 5 10 15
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Intensity

11. Interference and Diffraction

12. Bragg’s Law
n=2d.sin
n: Order of reflection
d: Plane spacing
=
: Bragg Angle
Path difference must be integral multiples of the wavelength
in=out
in out
2
2 2 2
a
h k l
 

13. Braggs Law


sin
2
n
d 


2
1
sin d


14. Geometry of Bragg’s law
 The incident beam, the normal to the reflection plane,
and the diffracted beam are always co-planar.
 The angle between the diffracted beam and the
transmitted beam is always 2 (usually measured).
 Sin  cannot be more than unity; this requires
nλ < 2d, for n=1, λ < 2d
λ should be less than twice the d spacing we want to study

15. Order of reflection
 Rewrite Bragg’s law λ=2 sin d/n
 A reflection of any order as a first order reflection from planes,
real or fictitious, spaced at a distance 1/n of the previous spacing
 Set d’ = d/n
 An nth order reflection from (hkl) planes of spacing d may be
considered as a first order reflection from the (nh nk nl) plane of
spacing d’ = d/n
λ=2d’ sin
*The term reflection is only notional due to symmetry between incoming and
outgoing beam w.r.t. plane normal, otherwise we are only talking of diffraction.

16. Reciprocal lattice vectors
Used to describe Fourier analysis of electron concentration
of the diffracted pattern.
Every crystal has associated with it a crystal lattice and a
reciprocal lattice.
A diffraction pattern of a crystal is the map of reciprocal
lattice of the crystal.

17. Real space Reciprocal space
Crystal Lattice Reciprocal Lattice
Crystal structure Diffraction pattern
Unit cell content Structure factor
x
y
y’
x’
y’
x’

18. Reciprocal space
Reciprocal lattice of FCC is BCC
and vice versa
)
(
*
)
(
*
)
(
*
c
b
a
b
a
c
c
b
a
a
c
b
c
b
a
c
b
a












a
b
c
100
001
010

19. Two Circle Diffractometer
 For polycrystalline Materials

20. Four Circle Diffractometer
For single crystals

21. 2 Circle diffratometer  2 and 
3 and 4 circle diffractometer  2θ, ω, φ, χ
 6 circle diffractometer  θ, φ, χ and δ, γ, µ
www.serc.carleton.edu/
Hong et al., Nuclear Instruments and Methods in Physics Research A 572 (2007) 942

22. NaCl crystals in a tube facing X-ray beam

23. Powder Diffractometer

24. Calculated Patterns for a Cubic Crystal
(100)
(110)
(200)
(111)
(210)
(211)
(220)
(330)
(221)
(310)
(311)
(222)
(320)
(321)
(400)
(410)

25. Structure Factor
2 ( )
1
n n n
N
i hu kv lw
hkl n
F f e   
 
− h,k,l : indices of the diffraction plane under consideration
− u,v,w : co-ordinates of the atoms in the lattice
− N : number of atoms
− fn : scattering factor of a particular type of atom
Bravais Lattice Reflections possibly present Reflections necessarily absent
Simple All None
Body Centered (h+k+l): Even (h+k+l): Odd
Face Centered h, k, and l unmixed i.e. all
odd or all even
h, k, and l: mixed
Intensity of the diffracted beam  |F|2

26. Systematic Absences
Simple Cubic (100), (110), (111), (200), (210), (211),
(220), (300), (221) ………
BCC (110), (200), (211), (220), (310), (222)….
FCC (111), (200), (220), (311)…..
Permitted Reflections

27. Diffraction Methods
Method Wavelength Angle Specimen
Laue Variable Fixed Single
Crystal
Rotating
Crystal
Fixed Variable (in
part)
Single
Crystal
Powder Fixed Variable Powder

28. Laue Method
• Uses Single crystal
• Uses White Radiation
• Used for determining crystal orientation and quality
Transmission Zone axis
crystal
Incident beam
Film
Reflection
Zone axis
crystal
Incident beam Film

29. Rotating Crystal Method
 Determination of unknown crystal structures

30. Diffraction from a variety of materials
(From “Elements of X-ray
Diffraction”, B.D. Cullity,
Addison Wesley)

31. Reality
0.9
cos



B
t
B
Crystallite size can be
calculated using
Scherrer Formula
Instrumental broadening must be subtracted
(From “Elements of X-ray Diffraction”, B.D. Cullity, Addison Wesley)

32. • polarization factor
• structure factor (F2)
• multiplicity factor
• Lorentz factor
• absorption factor
• temperature factor
For most materials the peaks and their intensity are
documented
 JCPDS
 ICDD
Intensity of diffracted beam

33. Name and formula
Reference code: 00-001-1260
PDF index name: Nickel
Empirical formula: Ni
Chemical formula: Ni
Crystallographic parameters
Crystal system: Cubic
Space group: Fm-3m
Space group number: 225
a (Å): 3.5175
b (Å): 3.5175
c (Å): 3.5175
Alpha (°): 90.0000
Beta (°): 90.0000
Gamma (°): 90.0000
Measured density (g/cm^3): 8.90
Volume of cell (10^6 pm^3): 43.52
Z: 4.00
RIR: -
Status, subfiles and quality
Status: Marked as deleted by ICDD
Subfiles: Inorganic
Quality: Blank (B)
References
Primary reference: Hanawalt et al., Anal. Chem., 10, 475, (1938)
Optical data: Data on Chem. for Cer. Use, Natl. Res. Council Bull. 107
Unit cell: The Structure of Crystals, 1st Ed.

34. http://ww1.iucr.org/cww-top/crystal.index.html
Stick pattern from JCPDS

35. Bulk electrodeposited nanocrystalline nickel
Lattice parameter, phase diagrams
Texture, Strain (micro and residual)
Size, microstructure (twins and
dislocations)
Actual Pattern

36. Powder X-ray diffraction
is essentially a misnomer and should be replaced by
Polycrystalline X-ray diffraction

37. Information in a Diffraction Pattern
 Phase Identification
 Crystal Size
 Crystal Quality
 Texture (to some extent)
 Crystal Structure

38. Analysis of Single Phase
Intensity
(a.u.)
2(˚) d (Å) (I/I1)*100
27.42 3.25 10
31.70 2.82 100
45.54 1.99 60
53.55 1.71 5
56.40 1.63 30
65.70 1.42 20
76.08 1.25 30
84.11 1.15 30
89.94 1.09 5
I1: Intensity of the strongest peak

39. Procedure
 Note first three strongest peaks at d1, d2, and d3
 In the present case: d1: 2.82; d2: 1.99 and d3: 1.63 Å
 Search JCPDS manual to find the d group belonging to the
strongest line: between 2.84-2.80 Å
 There are 17 substances with approximately similar d2 but only 4
have d1: 2.82 Å
 Out of these, only NaCl has d3: 1.63 Å
 It is NaCl……………Hurrah
Specimen and Intensities Substance File Number
2.829 1.999 2.26x 1.619 1.519 1.499 3.578 2.668 (ErSe)2Q 19-443
2.82x 1.996 1.632 3.261 1.261 1.151 1.411 0.891 NaCl 5-628
2.824 1.994 1.54x 1.204 1.194 2.443 5.622 4.892 (NH4)2WO2Cl4 22-65
2.82x 1.998 1.263 1.632 1.152 0.941 0.891 1.411 (BePd)2C 18-225
Caution: It could be much more tricky if the sample is oriented or textured or your goniometer is not
calibrated

40. Presence of Multiple phases
 More Complex
 Several permutations combinations possible
 e.g. d1; d2; and d3, the first three strongest lines
show several alternatives
 Then take any of the two lines together and match
 It turns out that 1st and 3rd strongest lies belong to
Cu and then all other peaks for Cu can be
separated out
 Now separate the remaining lines and normalize
the intensities
 Look for first three lines and it turns out that the
phase is Cu2O
 If more phases, more pain to solve 
d (Å) I/I1
3.01 5
2.47 72
2.13 28
2.09 100
1.80 52
1.50 20
1.29 9
1.28 18
1.22 4
1.08 20
1.04 3
0.98 5
0.91 4
0.83 8
0.81 10
*
*
*
*
*
*
*
Pattern for Cu
d (Å) I/I1
2.088 100
1.808 46
1.278 20
1.09 17
1.0436 5
0.9038 3
0.8293 9
0.8083 8
Remaining Lines
d (Å) I/I1
Observed Normalized
3.01 5 7
2.47 72 100
2.13 28 39
1.50 20 28
1.29 9 13
1.22 4 6
0.98 5 7
Pattern of Cu2O
d (Å) I/I1
3.020 9
2.465 100
2.135 37
1.743 1
1.510 27
1.287 17
1.233 4
1.0674 2
0.9795 4

41. Broadeing 2 2 tan
 

   
d
b
d
Lattice Strain
Non-uniform Strain
Uniform Strain
No Strain
do
2
2
2
  d  strain

42. Texture in Materials
 Grains with in a polycrystalline are not completely
randomly distributed
 Clustering of grains about some particular
orientation(s) to a certain degree
 Examples:
 Present in cold-rolled brass or steel sheets
 Cold worked materials tend to exhibit some texture after
recrystallization
 Affects the properties due to anisotropic nature

43. Texture
 Fiber Texture
 A particular direction [uvw] for all grains is more or less parallel to
the wire or fiber axis
 e.g. [111] fiber texture in Al cold drawn wire
 Double axis is also possible
 Example: [111] and [100] fiber textures in Cu wire
 Sheet Texture
 Most of the grains are oriented with a certain crystallographic plane
(hkl) roughly parallel to the sheet surface and certain direction [uvw]
parallel to the rolling direction
 Notation: (hkl)[uvw]

44. Texture in materials
 [uvw] i.e. perpendicular to
the surface of all grains is
parallel to a direction [uvw]










Also, if the direction [u1v1w1]
is parallel for all regions, the
structure is like a single
crystal
However, the direction [u1v1w1]
is not aligned for all regions,
the structure is like a mosaic
structure, also called as
Mosaic Texture

45. Degree of orientation
Substrate
Film
Side view
[uvw] corresponding
to planes parallel to
the surface
But what if the planes when looked from top have random orientation?
Top view

46. Pole Figure
 4 Peaks at ~50
 Excellent in-plane
orientation
1
1
1
1
2
2
2
2
1
1
1
2
2
2
3
3
3
1
2
3
 2 sets of peaks at ~ 5, 65
and 85°
 Indicating a doublet or
opposite twin growth
 3 sets of peaks
at ~ 35 and 85°
 indicating a
triplet or triple
twin growth
(117) Pole Figures for Bismuth Titanate Films
SrTiO3 (100) SrTiO3 (110) SrTiO3 (111)

47. Rocking Curve
 An useful method for evaluating the quality of oriented samples such as
epitaxial films
  is changed by rocking the sample but B is held constant
 Width of Rocking curve is a direct measure of the range of orientation present in
the irradiated area of the crystal
17.4 17.6 17.8 18.0 18.2
Intensity
(a.u.)
 ()
17.5 17.6 17.7 17.8
FWHM = 0.07°
(0010) Rocking curve of (001)-
oriented SrBi2Ta2O9 thin film
32.4 32.6 32.8 33.0 33.2
 ()
32.4 32.6 32.8 33.0 33.2
(2212) Rocking curve of (116)-
oriented SrBi2Ta2O9 thin film
FWHM = 0.171°
B 
Normal

48. Order Disorder Transformation
 Structure factor is dependent on the presence
of order or disorder within a material
 Present in systems such as Cu-Au, Ti-Al, Ni-
Fe
 Order-disorder transformation at specific
compositions upon heating/cooling across a
critical temperature
 Examples: Cu3Au, Ni3Fe

49. Order Disorder Transformation
 Structure factor is dependent on the presence
of order or disorder within a material.
 Complete Disorder
 Example: AB with A and B atoms
randomly distributed in the lattice
 Lattice positions: (000) and (½ ½ ½)
Atomic scattering factor
favj= ½ (fA+fB)
Structure Factor, F, is given by
F = Σf exp[2i (hu+kv+lw)]
= favj [1+e( i (h+k+l))]
= 2. favj when h+k+l is even
= 0 when h+k+l is odd
 The expected pattern is like a BCC crystal
A
B

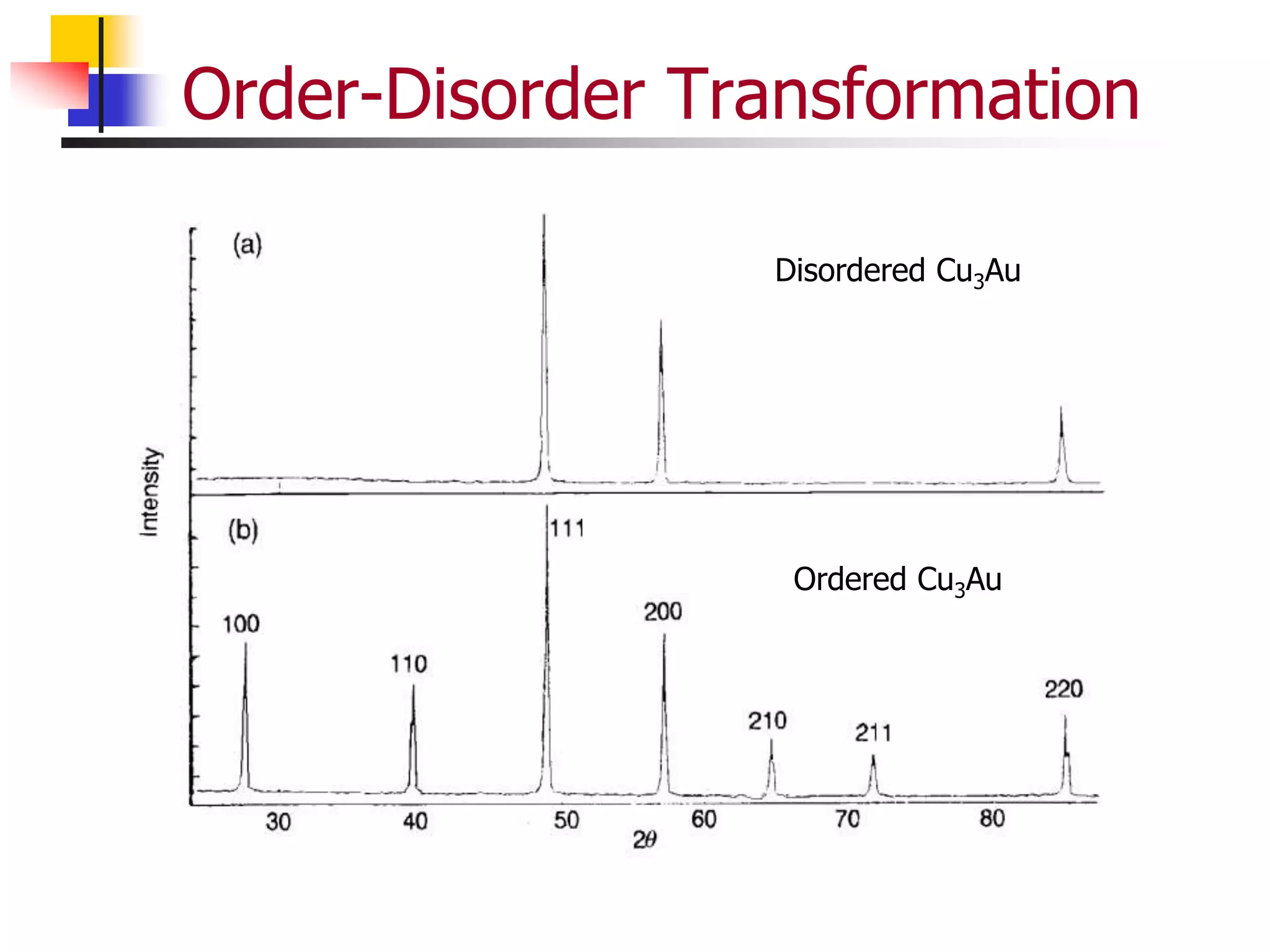
50. Order Disorder Transformation
 Complete Order
 Example: AB with A at (000) and B at (½ ½ ½)
Structure Factor, F, is given by
F = fA e[2i (h.0+k.0+l.0)]+ fA e[2i (h. ½+k. ½+l. ½)]
= fA+fB when h+k+l is even
= fA-fB when h+k+l is odd
 The expected pattern is not like a BCC crystal,
rather like a simple cubic crystal where all the
reflections are present.
 Extra reflections present are called as
superlattice reflections
A
B

51. Order-Disorder Transformation
Disordered Cu3Au
Ordered Cu3Au

52. Instrumentation

53. Diffractometer
 Source
 Optics
 Detector
Source Incident Beam
Optics
Sample Diffracted Beam
Optics
Detector
Incident Beam Part Diffracted Beam Part

54. Geometry and Configuration
Source Incident Beam
Optics
Sample Diffracted Beam
Optics
Detector
Incident Beam Part Diffracted Beam Part
 Theta-Theta Source and detector move θ, sample fixed
 Theta-2Theta Sample moves θ and detector 2θ , source fixed
 Vertical configuration Horizontal sample
 Horizontal configuration Vertical sample

55.  XYZ translation
 Z translation sample alignment
 Sample exactly on the diffractometer circle
 Knife edge or laser
 Video microscope with laser
 XY movement to choose
area of interest
Sample translation

56. X-ray generation
 X-ray tube (λ = 0.8-2.3 Ǻ)
 Rotating anode (λ = 0.8-2.3 Ǻ)
 Liquid metal
 Synchrotron (λ ranging from infrared to X-ray)

57. Electrons
X-rays
Be window
Metal anode
W cathode
X-ray tube

58. Small angle anode Large angle anode
Small focal spot Large focal spot

59.  Rotating anode of W or Mo for high flux
 Microfocus rotating anode 10 times brighter
 Liquid anode for high flux 100 times brighter
and small beam size
 Gallium and Gallium, indium, tin alloys
 Synchrotron provides intense beam but access is limited
 Brighter than a thousand suns

60.  High brilliance and coherence
 X-ray bulb emitting all radiations from IR to X-rays
http://www.coe.berkeley.edu/AST/srms
Synchrotron

61.  Moving charge emits radiation
 Electrons at v~c
 Bending magnet, wiggler and undulator
 Straight section wiggler and undulator
 Curved sections Bending magnet

62.  Filter to remove Kβ For eg. Ni filter for Cu Kβ
 Reduction in intensity of Kα
 Choice of proper thickness

63.  Slits To limit the size of beam (Divergence slits)
To alter beam profile
(Soller slit angular divergence )
 Narrow slits Lower intensity
+
Narrow peak

64. Mirror focusing and remove Kα2
Mono-chromator remove Kα2
Si Graphite

65. Beam Profile
Detector
Sample
Mirror
Source
Soller slit
Mirror
Detector
Sample
Source
Parallel beam
Para-focusing

66. Detector
Sample
Source
Point focus

67. Comparison
Parallel beam Para-focusing
X-rays are aligned X-rays are diverging
Lower intensity for bulk
samples
Higher intensity
Higher intensity for small
samples
Lower intensity
Instrumental broadening
independent of orientation
of diffraction vector with
specimen normal
Instrumental broadening
dependent of orientation of
diffraction vector with
specimen normal
Suitable for GI-XRD Suitable for Bragg-Brentano
Texture, stress Powder diffraction

68. Detectors
 Single photon detector (Point or 0D)
 scintillation detector NaI
 proportional counter, Xenon gas
 semiconductor
 Position sensitive detector (Linear or 1D)
 gas filled wire detectors, Xenon gas
 charge coupled devices (CCD)
 Area detectors (2D)
 wire
 CCD
 3D detector
X-ray photon
Photoelectron or
Electron-hole pair
Photomultiplier tube or
amplifier
Electrical signal

70.  Resolution: ability to distinguish between energies
 Energy proportionality: ability to produce signal proportioanl to
energy of x-ray photon detected
 Sensitivity: ability to detect low intensity levels
 Speed: to capture dynamic phenomenon
 Range: better view of the reciprocal space

71. Data collection and analysis
 Choose 2θ range
 Step size and time per step
 Hardware: slit size, filter, sample alignment
 Fast scan followed with a slower scan
 Look for fluorescence
 Collected data: Background subtraction, Kα2 stripping
 Normalize data for comparison I/Imax

72. Summary
 X-ray Diffraction is a very useful to characterize materials
for following information
 Phase analysis
 Lattice parameter determination
 Strain determination
 Texture and orientation analysis
 Order-disorder transformation
 and many more things
 Choice of correct type of method is critical for the kind of
work one intends to do.
 Powerful technique for thin film characterization