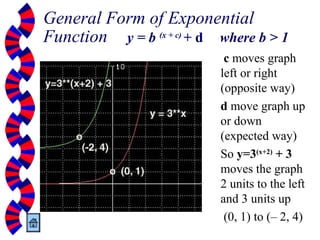
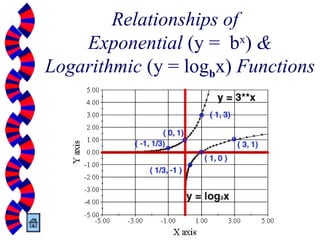
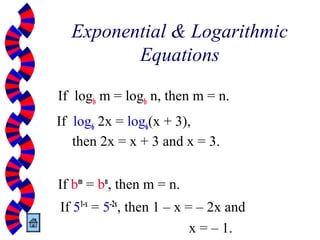The document provides an overview of exponential and logarithmic functions, detailing their definitions, properties, and relationships. It covers how to convert between exponents and logarithms, simplifies logarithmic expressions, and solves exponential and logarithmic equations. Key formulas, including general forms and properties of logarithms are also included to aid understanding.

1. Exponential & Logarithmic
Functions
Dr. Carol A. Marinas

2. Table of Contents
Exponential Functions
Logarithmic Functions
Converting between Exponents and
Logarithms
Properties of Logarithms
Exponential and Logarithmic Equations

3. General Form of Exponential
Function y = b x
where b > 1
Domain:
All reals
Range:
y > 0
x-intercept:
None
y-intercept:
(0, 1)

4. General Form of Exponential
Function y = b (x + c)
+ d where b > 1
c moves graph
left or right
(opposite way)
d move graph up
or down
(expected way)
So y=3(x+2)
+ 3
moves the graph
2 units to the left
and 3 units up
(0, 1) to (– 2, 4)

5. Relationships of
Exponential (y = bx
) &
Logarithmic (y = logbx) Functions
y = logbx is the
inverse of y = bx
Domain: x > 0
Range: All Reals
x-intercept: (1, 0)
y-intercept: None
y = bx
Domain: All Reals
Range: y > 0
x-intercept: None
y-intercept: (0, 1)

6. Relationships of
Exponential (y = bx
) &
Logarithmic (y = logbx) Functions

7. Converting between
Exponents & Logarithms
BASEEXPONENT
= POWER
42
= 16
4 is the base. 2 is the exponent.
16 is the power.
As a logarithm,
logBASEPOWER=EXPONENT
log 416 = 2

8. Logarithmic Abbreviations
log10 x = log x (Common log)
logex = ln x (Natural log)
e = 2.71828...

9. Properties of Logarithms
logb(MN)= logbM + logbN
Ex: log4(15)= log45 + log43
logb(M/N)= logbM – logbN
Ex: log3(50/2)= log350 – log32
logbMr
= r logbM
Ex: log7 103
= 3 log7 10
logb(1/M) = logbM-1
= –1 logbM = – logbM
log11(1/8) = log118-1
= – 1 log118 = – log11 8

10. Properties of Logarithms
(Shortcuts)
logb1 = 0 (because b0
= 1)
logbb = 1 (because b1
= b)
logbbr
= r (because br
= br
)
blogbM
= M (because logbM = logbM)

11. Examples of Logarithms
Simplify log 7 + log 4 – log 2 =
log 7*4 = log 14
2
Simplify ln e2
=
2 ln e = 2 logee = 2 * 1 = 2
Simplify e 4ln3-3ln4
=
e ln34-ln43
= e ln81/64
= e loge81/64
= 81/64

12. Change-of-Base Formula
logam
logbm = --------
logab
log712 = log 12
log 7
OR
log712 = ln 12
ln 7

13. Exponential & Logarithmic
Equations
If logb m = logb n, then m = n.
If log6 2x = log6(x + 3),
then 2x = x + 3 and x = 3.
If bm
= bn
, then m = n.
If 51-x
= 5-2x
, then 1 – x = – 2x and
x = – 1.

14. If your variable is in the
exponent…..
Isolate the base-exponent term.
Write as a log. Solve for the variable.
Example: 4x+3
= 7
log 4 7 = x + 3 and – 3 + log 4 7 = x
OR with change of bases:
x = – 3 + log 7
log 4
Another method is to take the LOG of
both sides.

15. Logarithmic Equations
Isolate to a single log term.
Convert to an exponent.
Solve equation.
Example: log x + log (x – 15) = 2
log x(x – 15) = 2 so 102
= x (x – 15) and
100 = x2
– 15x and 0 = x2
– 15x – 100
So 0 = (x – 20) (x + 5) so x = 20 or – 5

16. That’s All Folks !