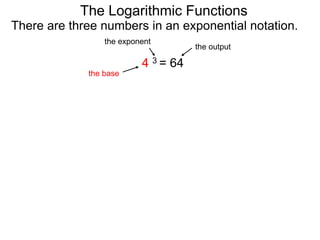
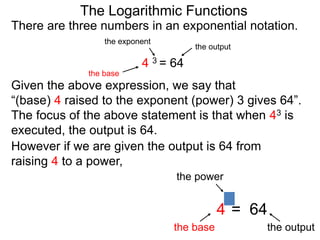
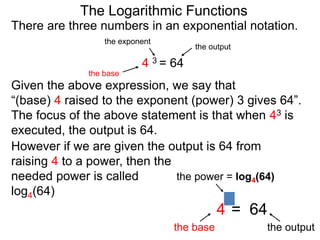
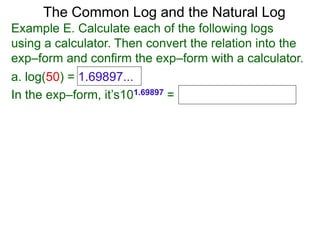
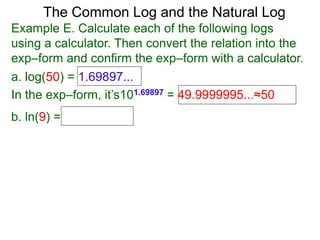
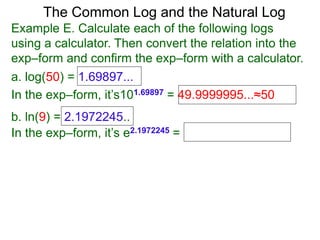
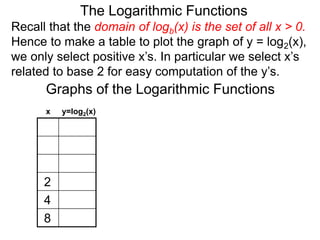
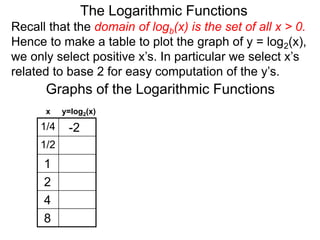
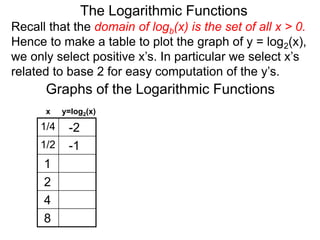
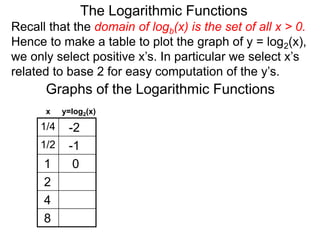
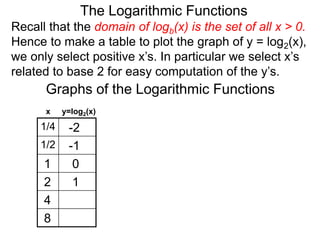
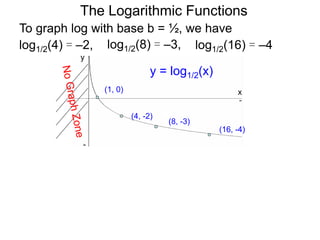
The document discusses logarithmic functions and how they relate to exponential forms. It explains that logarithmic functions take the form logb(y)=x, where b is the base, y is the output, and x is the exponent. This is equivalent to the exponential form bx=y. The document provides examples of converting between exponential and logarithmic forms using different bases. It also notes that the base and output must be positive numbers for logarithmic functions.

1. The Logarithmic Functions

2. There are three numbers in an exponential notation.
The Logarithmic Functions
4 3 = 64

3. There are three numbers in an exponential notation.
The Logarithmic Functions
the base
4 3 = 64

4. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
4 3 = 64

5. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64

6. There are three numbers in an exponential notation.
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64

7. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The focus of the above statement is that when 43 is
executed, the output is 64.

8. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64
However if we are given the output is 64 from
raising 4 to a power,
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The focus of the above statement is that when 43 is
executed, the output is 64.

9. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64
However if we are given the output is 64 from
raising 4 to a power,
the power
the base the output
4 = 64
3
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The focus of the above statement is that when 43 is
executed, the output is 64.

10. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64
However if we are given the output is 64 from
raising 4 to a power, then the
needed power is called
log4(64)
the power = log4(64)
the base the output
4 = 64
3
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The focus of the above statement is that when 43 is
executed, the output is 64.

11. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64
However if we are given the output is 64 from
raising 4 to a power, then the
needed power is called
log4(64) which is 3.
the power = log4(64)
the base the output
4 = 64
3
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The focus of the above statement is that when 43 is
executed, the output is 64.

12. There are three numbers in an exponential notation.
The Logarithmic Functions
the exponent
the base
the output
4 3 = 64
However if we are given the output is 64 from
raising 4 to a power, then the
needed power is called
log4(64) which is 3.
the power = log4(64)
the base the output
4 = 64
3
or that log4(64) = 3 and we say
that “log–base–4 of 64 is 3”.
Given the above expression, we say that
“(base) 4 raised to the exponent (power) 3 gives 64”.
The focus of the above statement is that when 43 is
executed, the output is 64.

13. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.”,

14. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.” The expression
“64 = 43”
contains the same information as
“log4(64) = 3”.

15. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.” The expression
“64 = 43”
contains the same information as
“log4(64) = 3”.
The expression “64 = 43” is called the exponential form
and “log4(64) = 3” is called the logarithmic form of the
expressed relation.

16. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.” The expression
“64 = 43”
contains the same information as
“log4(64) = 3”.
The expression “64 = 43” is called the exponential form
and “log4(64) = 3” is called the logarithmic form of the
expressed relation.
In general, we say that
“log–base–b of y is x” or
logb(y) = x

17. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.” The expression
“64 = 43”
contains the same information as
“log4(64) = 3”.
The expression “64 = 43” is called the exponential form
and “log4(64) = 3” is called the logarithmic form of the
expressed relation.
In general, we say that
“log–base–b of y is x” or
logb(y) = x if y = bx (b > 0).

18. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.” The expression
“64 = 43”
contains the same information as
“log4(64) = 3”.
The expression “64 = 43” is called the exponential form
and “log4(64) = 3” is called the logarithmic form of the
expressed relation.
In general, we say that
“log–base–b of y is x” or
logb(y) = x if y = bx (b > 0).
the power = logb(y)
the base the output
b = y
x

19. The Logarithmic Functions
Just as the sentence
“Bart's dad is Homer.”
contains the same information as
“Homer's son is Bart.” The expression
“64 = 43”
contains the same information as
“log4(64) = 3”.
The expression “64 = 43” is called the exponential form
and “log4(64) = 3” is called the logarithmic form of the
expressed relation.
In general, we say that
“log–base–b of y is x” or
logb(y) = x if y = bx (b > 0),
i.e. logb(y) is the exponent x.
the power = logb(y)
the base the output
b = y
x

20. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.

21. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.

22. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
exp–form

23. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
Their corresponding
log–form are differentiated
by the bases and the
different exponents
required.
43 → 64
82 → 64
26 → 64
exp–form log–form

24. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64)
log8(64)
log2(64)
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.

25. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
Their corresponding
log–form are differentiated
by the bases and the
different exponents
required.
43 → 64
82 → 64
26 → 64
log4(64) →
log8(64) →
log2(64) →
exp–form log–form

26. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64) → 3
log8(64) →
log2(64) →
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.

27. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64) → 3
log8(64) → 2
log2(64) →
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.

28. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64) → 3
log8(64) → 2
log2(64) → 6
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.

29. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64) → 3
log8(64) → 2
log2(64) → 6
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.
Both numbers b and y appearing in the log notation
“logb(y)” must be positive.

30. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64) → 3
log8(64) → 2
log2(64) → 6
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.
Both numbers b and y appearing in the log notation
“logb(y)” must be positive. Switch to x as the input,
the domain of logb(x) is the set D = {x l x > 0 }.

31. The Logarithmic Functions
When working with the exponential form or the
logarithmic expressions, always identify the base
number b first.
All the following exponential expressions yield 64.
43 → 64
82 → 64
26 → 64
log4(64) → 3
log8(64) → 2
log2(64) → 6
exp–form log–formTheir corresponding
log–form are differentiated
by the bases and the
different exponents
required.
Both numbers b and y appearing in the log notation
“logb(y)” must be positive. Switch to x as the input,
the domain of logb(x) is the set D = {x l x > 0 }.
We would get an error message if we execute
log2(–1) with software.

32. The Logarithmic Functions
To convert the exp-form to the log–form:
b = y
x

33. The Logarithmic Functions
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
Identity the base and the
correct log–function

34. The Logarithmic Functions
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
insert the exponential
output.

35. The Logarithmic Functions
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
The log–output is the
required exponent.

36. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16
b. w = u2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

37. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

38. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

39. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

40. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

41. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

42. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→

43. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
→
To convert the log–form to the exp–form:
logb( y ) = x
logb( y ) = x

44. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→
logb( y ) = x

45. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→
logb( y ) = x

46. The Logarithmic Functions
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→
logb( y ) = x

47. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2
b. 2w = logv(a – b)
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

48. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

49. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

50. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

51. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)  v2w = a – b
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

52. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)  v2w = a – b
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

53. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)  v2w = a – b
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→

54. The Logarithmic Functions
Example B. Rewrite the log-form into the exp-form.
a. log3(1/9) = –2  3-2 = 1/9
b. 2w = logv(a – b)  v2w = a – b
Example A. Rewrite the exp-form into the log-form.
a. 42 = 16  log4(16) = 2
b. w = u2+v  logu(w) = 2+v
To convert the exp-form to the log–form:
b = y
x
logb( y ) = x→
To convert the log–form to the exp–form:
b = y
x
logb( y ) = x→
The output of logb(x), i.e. the exponent in the defined
relation, may be positive or negative.

55. The Logarithmic Functions
Example C.
a. Rewrite the exp-form into the log-form.
4–3 = 1/64
8–2 = 1/64
log4(1/64) = –3
log8(1/64) = –2
exp–form log–form
b. Rewrite the log-form into the exp-form.
(1/2)–2 = 4log1/2(4) = –2
log1/2(8) = –3
exp–formlog–form
(1/2)–3 = 8

56. The Logarithmic Functions
The Common Log and the Natural Log
Example C.
a. Rewrite the exp-form into the log-form.
4–3 = 1/64
8–2 = 1/64
log4(1/64) = –3
log8(1/64) = –2
exp–form log–form
b. Rewrite the log-form into the exp-form.
(1/2)–2 = 4log1/2(4) = –2
log1/2(8) = –3
exp–formlog–form
(1/2)–3 = 8

57. The Logarithmic Functions
Base 10 is called the common base.
The Common Log and the Natural Log
Example C.
a. Rewrite the exp-form into the log-form.
4–3 = 1/64
8–2 = 1/64
log4(1/64) = –3
log8(1/64) = –2
exp–form log–form
b. Rewrite the log-form into the exp-form.
(1/2)–2 = 4log1/2(4) = –2
log1/2(8) = –3
exp–formlog–form
(1/2)–3 = 8

58. The Logarithmic Functions
Base 10 is called the common base. Log with
base10, written as log(x) without the base number b,
is called the common log,
The Common Log and the Natural Log
Example C.
a. Rewrite the exp-form into the log-form.
4–3 = 1/64
8–2 = 1/64
log4(1/64) = –3
log8(1/64) = –2
exp–form log–form
b. Rewrite the log-form into the exp-form.
(1/2)–2 = 4log1/2(4) = –2
log1/2(8) = –3
exp–formlog–form
(1/2)–3 = 8

59. The Logarithmic Functions
Base 10 is called the common base. Log with
base10, written as log(x) without the base number b,
is called the common log, i.e. log(x) is log10(x).
The Common Log and the Natural Log
Example C.
a. Rewrite the exp-form into the log-form.
4–3 = 1/64
8–2 = 1/64
log4(1/64) = –3
log8(1/64) = –2
exp–form log–form
b. Rewrite the log-form into the exp-form.
(1/2)–2 = 4log1/2(4) = –2
log1/2(8) = –3
exp–formlog–form
(1/2)–3 = 8

60. Base e is called the natural base.
The Common Log and the Natural Log

61. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log,
The Common Log and the Natural Log

62. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log

63. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000
ln(1/e2) = -2
ert =
log(1) = 0
A
P

64. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000 log(1000) = 3
ln(1/e2) = -2
ert =
log(1) = 0
A
P

65. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000 log(1000) = 3
e-2 = 1/e2 ln(1/e2) = -2
ert =
log(1) = 0
A
P

66. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000 log(1000) = 3
e-2 = 1/e2 ln(1/e2) = -2
ert = ln( ) = rt
log(1) = 0
A
P
A
P

67. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000 log(1000) = 3
e-2 = 1/e2 ln(1/e2) = -2
ert = ln( ) = rt
100 = 1 log(1) = 0
A
P
A
P

68. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000 log(1000) = 3
e-2 = 1/e2 ln(1/e2) = -2
ert = ln( ) = rt
100 = 1 log(1) = 0
A
P
A
P
Most log and powers can’t be computed efficiently by
hand.

69. Base e is called the natural base.
Log with base e is written as ln(x) and it’s called
the natural log, i.e. In(x) is loge(x).
The Common Log and the Natural Log
Example D. Convert to the other form.
exp-form log-form
103 = 1000 log(1000) = 3
e-2 = 1/e2 ln(1/e2) = -2
ert = ln( ) = rt
100 = 1 log(1) = 0
A
P
A
P
Most log and powers can’t be computed efficiently by
hand. We need a calculation device to extract
numerical solutions.

70. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) =

71. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...

72. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 =

73. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50

74. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) =

75. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..

76. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
In the exp–form, it’s e2.1972245 =

77. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
In the exp–form, it’s e2.1972245 = 8.9999993...≈ 9

78. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
c. Calculate the power using a calculator.
Then convert the relation into the log–form and
confirm the log–form by the calculator.
e4.3 =
In the exp–form, it’s e2.1972245 = 8.9999993...≈ 9

79. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
c. Calculate the power using a calculator.
Then convert the relation into the log–form and
confirm the log–form by the calculator.
e4.3 = 73.699793..
In the exp–form, it’s e2.1972245 = 8.9999993...≈ 9

80. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
c. Calculate the power using a calculator.
Then convert the relation into the log–form and
confirm the log–form by the calculator.
e4.3 = 73.699793..→ In(73.699793) =
In the exp–form, it’s e2.1972245 = 8.9999993...≈ 9

81. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
c. Calculate the power using a calculator.
Then convert the relation into the log–form and
confirm the log–form by the calculator.
e4.3 = 73.699793..→ In(73.699793) = 4.299999..≈ 4.3
In the exp–form, it’s e2.1972245 = 8.9999993...≈ 9

82. The Common Log and the Natural Log
Example E. Calculate each of the following logs
using a calculator. Then convert the relation into the
exp–form and confirm the exp–form with a calculator.
a. log(50) = 1.69897...
In the exp–form, it’s101.69897 = 49.9999995...≈50
b. ln(9) = 2.1972245..
c. Calculate the power using a calculator.
Then convert the relation into the log–form and
confirm the log–form by the calculator.
e4.3 = 73.699793..→ In(73.699793) = 4.299999..≈ 4.3
Your turn. Follow the instructions in part c for 10π.
In the exp–form, it’s e2.1972245 = 8.9999993...≈ 9

83. Equations may be formed with log–notation.
The Common Log and the Natural Log

84. Equations may be formed with log–notation. Often we
need to restate them in the exp–form.
The Common Log and the Natural Log

85. Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

86. Example F. Solve for x
a. log9(x) = –1
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

87. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

88. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

89. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
b. logx(9) = –2
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

90. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
b. logx(9) = –2
Drop the log and get 9 = x–2,
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

91. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
b. logx(9) = –2
Drop the log and get 9 = x–2, i.e. 9 =
1
x2
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

92. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
b. logx(9) = –2
Drop the log and get 9 = x–2, i.e. 9 =
So 9x2 = 1
1
x2
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

93. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
b. logx(9) = –2
Drop the log and get 9 = x–2, i.e. 9 =
So 9x2 = 1
x2 = 1/9
x = 1/3 or x= –1/3
1
x2
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

94. Example F. Solve for x
a. log9(x) = –1
Drop the log and get x = 9–1.
So x = 1/9
b. logx(9) = –2
Drop the log and get 9 = x–2, i.e. 9 =
So 9x2 = 1
x2 = 1/9
x = 1/3 or x= –1/3
Since the base b > 0, so x = 1/3 is the only solution.
1
x2
Equations may be formed with log–notation. Often we
need to restate them in the exp–form. We say we
"drop the log" when this step is taken.
The Common Log and the Natural Log

95. The Logarithmic Functions
Graphs of the Logarithmic Functions
Recall that the domain of logb(x) is the set of all x > 0.

96. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4
1/2
1
2
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s.

97. The Logarithmic Functions
Graphs of the Logarithmic Functions
2
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

98. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4
1/2
1
2
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

99. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4 -2
1/2
1
2
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

100. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4 -2
1/2 -1
1
2
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

101. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4 -2
1/2 -1
1 0
2
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

102. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4 -2
1/2 -1
1 0
2 1
4
8
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

103. The Logarithmic Functions
Graphs of the Logarithmic Functions
1/4 -2
1/2 -1
1 0
2 1
4 2
8 3
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.

104. The Logarithmic Functions
(1, 0)
(2, 1)
(4, 2)
(8, 3)
(16, 4)
(1/2, -1)
(1/4, -2)
y=log2(x)
Graphs of the Logarithmic Functions
1/4 -2
1/2 -1
1 0
2 1
4 2
8 3
x y=log2(x)
Recall that the domain of logb(x) is the set of all x > 0.
Hence to make a table to plot the graph of y = log2(x),
we only select positive x’s. In particular we select x’s
related to base 2 for easy computation of the y’s.
x
y

105. The Logarithmic Functions
To graph log with base b = ½, we have
log1/2(4) = –2, log1/2(8) = –3, log1/2(16) = –4

106. The Logarithmic Functions
x
y
(1, 0)
(8, -3)
To graph log with base b = ½, we have
log1/2(4) = –2, log1/2(8) = –3, log1/2(16) = –4
(4, -2)
(16, -4)
y = log1/2(x)

107. The Logarithmic Functions
x
y
(1, 0)
(8, -3)
To graph log with base b = ½, we have
log1/2(4) = –2, log1/2(8) = –3, log1/2(16) = –4
(4, -2)
(16, -4)
y = log1/2(x)
x x
y
(1, 0)(1, 0)
y = logb(x), b > 1
y = logb(x), 1 > b
Here are the general shapes of log–functions.
y
(b, 1)
(b, 1)

108. 1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:

109. 1. logb(1) = 01. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:

110. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:

111. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:

112. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:

113. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:
We veryify part 2: logb(xy) = logb(x) + logb(y), x, y > 0.
Proof:

114. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:
We veryify part 2: logb(xy) = logb(x) + logb(y), x, y > 0.
Proof:
Let x and y be two positive numbers.

115. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:
We veryify part 2: logb(xy) = logb(x) + logb(y), x, y > 0.
Proof:
Let x and y be two positive numbers. Let logb(x) = r
and logb(y) = t, which in exp-form are x = br and y = bt.

116. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:
We veryify part 2: logb(xy) = logb(x) + logb(y), x, y > 0.
Proof:
Let x and y be two positive numbers. Let logb(x) = r
and logb(y) = t, which in exp-form are x = br and y = bt.
Therefore x·y = br+t,

117. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:
We veryify part 2: logb(xy) = logb(x) + logb(y), x, y > 0.
Proof:
Let x and y be two positive numbers. Let logb(x) = r
and logb(y) = t, which in exp-form are x = br and y = bt.
Therefore x·y = br+t, which in log-form is
logb(x·y) = r + t = logb(x)+logb(y).

118. 1. logb(1) = 0
2. logb(x·y) = logb(x)+logb(y)
3. logb( ) = logb(x) – logb(y)
4. logb(xt) = t·logb(x)
x
y
1. b0 = 1
2. br · bt = br+t
3. = br-t
4. (br)t = brt
bt
br
Properties of Logarithm
Recall the following
Rules of Exponents:
The corresponding
Rules of Logs are:
We veryify part 2: logb(xy) = logb(x) + logb(y), x, y > 0.
Proof:
Let x and y be two positive numbers. Let logb(x) = r
and logb(y) = t, which in exp-form are x = br and y = bt.
Therefore x·y = br+t, which in log-form is
logb(x·y) = r + t = logb(x)+logb(y).
The other rules may be verified similarly.

119. Example G.
3x2
y
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).

120. 3x2
y
log( ) = log( ),3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
Example G.

121. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
Example G.

122. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule
= log(3) + log(x2)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
Example G.

123. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule power rule
= log(3) + log(x2) – ½ log(y)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
Example G.

124. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule power rule
= log(3) + log(x2) – ½ log(y)
= log(3) + 2log(x) – ½ log(y)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
Example G.

125. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule power rule
= log(3) + log(x2) – ½ log(y)
= log(3) + 2log(x) – ½ log(y)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
b. Combine log(3) + 2log(x) – ½ log(y) into one log.
Example G.

126. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule power rule
= log(3) + log(x2) – ½ log(y)
= log(3) + 2log(x) – ½ log(y)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
log(3) + 2log(x) – ½ log(y) power rule
= log(3) + log(x2) – log(y1/2)
b. Combine log(3) + 2log(x) – ½ log(y) into one log.
Example G.

127. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule power rule
= log(3) + log(x2) – ½ log(y)
= log(3) + 2log(x) – ½ log(y)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
log(3) + 2log(x) – ½ log(y) power rule
= log(3) + log(x2) – log(y1/2) product rule
= log (3x2) – log(y1/2)
b. Combine log(3) + 2log(x) – ½ log(y) into one log.
Example G.

128. 3x2
y
log( ) = log( ), by the quotient rule
= log (3x2) – log(y1/2)
product rule power rule
= log(3) + log(x2) – ½ log(y)
= log(3) + 2log(x) – ½ log(y)
3x2
y
3x2
y1/2
Properties of Logarithm
a. Write log( ) in terms of log(x) and log(y).
log(3) + 2log(x) – ½ log(y) power rule
= log(3) + log(x2) – log(y1/2) product rule
= log (3x2) – log(y1/2)= log( )3x2
y1/2
b. Combine log(3) + 2log(x) – ½ log(y) into one log.
Example G.
quotient rule

129. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x.
Properties of Logarithm

130. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Properties of Logarithm

131. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
Properties of Logarithm

132. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b

133. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b
Example H. Simplify
a. log2(2-5) =
b. 8log (xy) =
c. e2+ln(7) =
8

134. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b
Example H. Simplify
a. log2(2-5) = -5
b. 8log (xy) =
c. e2+ln(7) =
8

135. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b
Example H. Simplify
a. log2(2-5) = -5
b. 8log (xy) = xy
c. e2+ln(7) =
8

136. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b
Example H. Simplify
a. log2(2-5) = -5
b. 8log (xy) = xy
c. e2+ln(7) = e2·eln(7)
8

137. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b
Example H. Simplify
a. log2(2-5) = -5
b. 8log (xy) = xy
c. e2+ln(7) = e2·eln(7) = 7e2
8

138. Recall that given a pair of inverse functions, f and f -1,
then f(f -1(x)) = x and f -1(f(x)) = x. Let expb(x) ≡ bx.
Since expb(x) and logb(x) is a pair of inverse functions,
we have that:
a. logb(expb(x)) = x or logb(bx) = x
b. expb(logb(x)) = x or blog (x) = x
Properties of Logarithm
b
Example H. Simplify
a. log2(2-5) = -5
b. 8log (xy) = xy
c. e2+ln(7) = e2·eln(7) = 7e2
8
Logb(x) and expb(x) along with trig. and inverse trig.
functions are the most important explicit inverse
function pairs in mathematics.

139. 1.
Exercise A. Rewrite the following exp-form into the log-form.
2. 3.
4. 5. 6.
7. 8. 9.
10.
The Logarithmic Functions
Exercise B. Rewrite the following log–form into the exp-form.
52 = 25 33 = 27
1/25 = 5–2 x3 = y
y3 = x ep = a + b
e(a + b) = p 10x–y = z11. 12.
1/25 = 5–2
1/27 = 3–3
1/a = b–2
A = e–rt
log3(1/9) = –2 –2 = log4(1/16)13. 14. log1/3(9) = –215.
2w = logv(a – b)17. logv(2w) = a – b18.log1/4(16) = –216.
log (1/100) = –2 1/2 = log(√10)19. 20. ln(1/e2) = –221.
rt = ln(ert)23. ln(1/√e) = –1/224.log (A/B) = 322.

140. Exercise C. Convert the following into the exponential form
then solve for x.
The Logarithmic Functions
logx(9) = 2 x = log2(8)1. 2. log3(x) = 23.
5. 6.4.
7. 9.8.
logx(x) = 2 2 = log2(x) logx(x + 2) = 2
log1/2(4) = x 4 = log1/2(x) logx(4) = 1/2
11. 12.10.
13. 15.14.
ln(x) = 2 2 = log(x) log(4x + 15) = 2
In(x) = –1/2 a = In(2x – 3) log(x2 – 15x) = 2

141. Ex. D
Disassemble the following log expressions in terms of
sums and differences logs as much as possible.
Properties of Logarithm
5. log2(8/x4) 6. log (√10xy)
y√z3
2. log (x2y3z4)
4. log ( )
x2
1. log (xyz)
7. log (10(x + y)2) 8. ln ( )
√t
e2
9. ln ( )
√e
t2
10. log (x2 – xy) 11. log (x2 – y2) 12. ln (ex+y)
13. log (1/10y) 14. log ( )x2 – y2
x2 + y2
15. log (√100y2)
3
3. log ( )
z4
x2y3
16. ln( )x2 – 4
√(x + 3)(x + 1)
17. ln( )(x2 + 4)2/3
(x + 3)–2/3(x + 1) –3/4

142. E. Assemble the following expressions into one log.
Properties of Logarithm
2. log(x) – log(y) + log(z) – log(w)
3. –log(x) + 2log(y) – 3log(z) + 4log(w)
4. –1/2 log(x) –1/3 log(y) + 1/4 log(z) – 1/5 log(w)
1. log(x) + log(y) + log(z) + log(w)
6. –1/2 log(x – 3y) – 1/4 log(z + 5w)
5. log(x + y) + log(z + w)
7. ½ ln(x) – ln(y) + ln(x + y)
8. – ln(x) + 2 ln(y) + ½ ln(x – y)
9. 1 – ln(x) + 2 ln(y)
10. ½ – 2ln(x) + 1/3 ln(y) – ln(x + y)

143. Continuous Compound Interest
F. Given the following projection of the world
populations, find the growth rate between each
two consecutive data.
Is there a trend in the growth rates used?

144. (Answers to the odd problems) Exercise A.
Exercise B.
13. 3−2 = 1/9 15.
1
3
−2
= 9 17. 𝑦2𝑤
= 𝑎 − 𝑏
19. 10−2 = 1/100 21. 𝑒−2 = 1/𝑒2 23. 𝑒 𝑟𝑡 = 𝑒 𝑟𝑡
1. 𝑙𝑜𝑔5 25 = 2 3. 𝑙𝑜𝑔3 27 = 3
7. 𝑙𝑜𝑔 𝑦(𝑥) = 3 9. 𝑙𝑜𝑔 𝑒 𝑎 + 𝑏 = 𝑝
5. 𝑙𝑜𝑔391/27) = −3
11. 𝑙𝑜𝑔 𝑒 𝐴 = −𝑟𝑡
Exercise C.
1. 𝑥 = 3 3. 𝑥 = 9 5. 𝑥 = 4 7. 𝑥 = −2
9. 𝑥 = 16 11. 𝑥 = 100 13. 𝑥 =
1
𝑒
15. 𝑥 = −5, 𝑥 = 20
The Logarithmic Functions

145. Exercise D.
5. 𝑙𝑜𝑔2 8 − 4𝑙𝑜𝑔2(𝑥)
1. log(𝑥) + log(𝑦) + log(𝑧)
7. log(10) + 2log(𝑥 + 𝑦)
9. 2ln(𝑡) − 1/2ln(𝑒) 11. log(𝑥2 – 𝑦2)
13. log(1) − 𝑦𝑙𝑜𝑔(10)
3. 2log(𝑥) + 3log(𝑦) − 4log(𝑧)
15. 1/3log(100) + 2/3log(𝑦)
17. 2/3ln(𝑥 + 4) + 2/3ln(𝑥 + 3) + 3/4ln(𝑥 + 1)
Exercise E.
3. log
𝑦2 𝑤4
𝑥𝑧3
1. log(𝑥𝑦𝑧𝑤) 5. 𝑙𝑜𝑔 (𝑥 + 𝑦)(𝑧 + 𝑤)
7. 𝑙𝑛
𝑥(𝑥+𝑦)
𝑦
9. 𝑙𝑛
𝑒𝑦2
𝑥
Properties of Logarithm