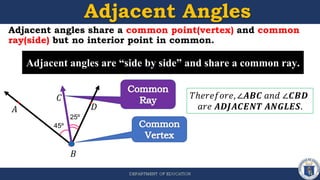
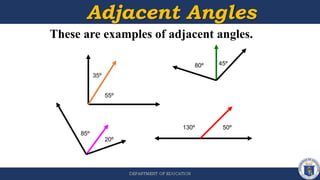
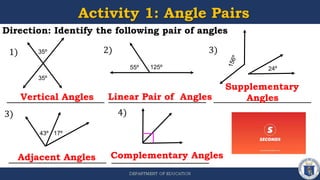
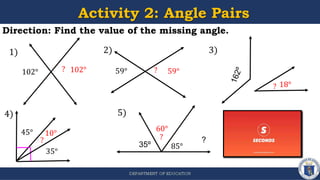
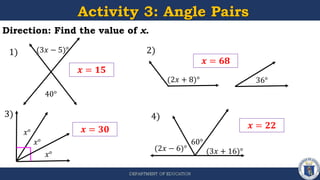
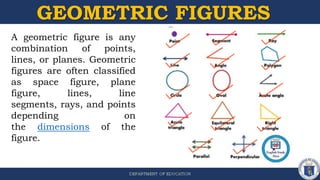
1) The document defines different types of angle pairs including adjacent angles, vertical angles, complementary angles, supplementary angles, and linear pairs of angles. It provides examples and explanations of each. 2) Activities are included for students to identify angle pair types and find missing angle measures using properties of different angle pairs. 3) The objectives are to define angle pairs, derive relationships between geometric figures using inductive reasoning involving angle pairs, and solve problems involving angle pairs.

1. PRAYER

2. WATCHING VIDEO LESSON

3. 4 PICS ONE
WORD

4. R E L T I N S I P
__ __
A O H
__

5. GEOMETRIC __
F __
I R
U
G ES

6. A __ G __ E
N L

7. I __ S
P __
A R

8. Relationship of
Geometric Figures:
Angle Pairs
MARK ATNHONY F. GUIRA
CUBAL INTEGRATED SCHOOL

9. OBJECTIVES:
At the end of this lesson, you will be able to:
1) Define angle pairs;
2) Derive the relationship of geometric figures using
inductive reasoning: angle pairs;
3) Solve problems involving angle pairs.

10. GEOMETRIC FIGURES
A geometric figure is any
combination of points,
lines, or planes. Geometric
figures are often classified
as space figure, plane
figure, lines, line
segments, rays, and points
depending on
the dimensions of the
figure.

11. ANGLE PAIRS
Angle pairs are angles that appear in twos to display a
certain geometrical property.
Adjacent Angles
Vertical Angles
Complementary Angles
Supplementary Angles
Linear Pair of Angles

12. To denote the measure of an angle we write an
“m” in front of the symbol for the angle.
𝑨𝒄𝒖𝒕𝒆 𝑨𝒏𝒈𝒍𝒆 𝑹𝒊𝒈𝒉𝒕 𝑨𝒏𝒈𝒍𝒆
𝑶𝒃𝒕𝒖𝒔𝒆 𝑨𝒏𝒈𝒍𝒆
𝑺𝒕𝒓𝒂𝒊𝒈𝒉𝒕 𝑨𝒏𝒈𝒍𝒆
Here are some common angles and their measurements.
4
4 180
m  
2 90
m  
2
1
1 45
m  
3 135
m  
3
“the measure of angle 1
is equal to 45 degrees”

13. Congruent Angles
• So, two angles are congruent if and only if
they have the same measure.
∠𝐴𝐵𝐶 ≅ ∠XYZ if and only if 𝑚∠𝐴𝐵𝐶 = 𝑚∠𝑋𝑌𝑍.
Means
Congruent
Means Equal
• So, the angles are congruent.
𝐴
𝑋
𝐸𝑥𝑎𝑚𝑝𝑙𝑒:
𝐵
𝐶
𝑌
𝑍
30°
30°

14. ANGLE PAIRS

15. Adjacent Angles
Adjacent angles share a common point(vertex) and common
ray(side) but no interior point in common.
Adjacent angles are “side by side” and share a common ray.
45º
𝐴
25º
𝐵
𝐶
𝐷
𝑇ℎ𝑒𝑟𝑒𝑓𝑜𝑟𝑒, ∠𝑨𝑩𝑪 𝑎𝑛𝑑 ∠𝑪𝑩𝑫
𝑎𝑟𝑒 𝑨𝑫𝑱𝑨𝑪𝑬𝑵𝑻 𝑨𝑵𝑮𝑳𝑬𝑺.

16. Adjacent Angles
These are examples of adjacent angles.
55º
35º
50º
130º
80º 45º
85º
20º

17. Adjacent Angles
These angles are NOT adjacent.
45º
55º
50º
100º
35º
35º

18. Vertical Angles
Two opposite angles formed by intersecting lines and have no
common sides but share a common vertex.
Four angles are formed at the point of
intersection.
∠𝑨𝑷𝑪
∠𝑨𝑷𝑩
∠𝑩𝑷𝑫
∠𝑪𝑷𝑫
≅
≅
Vertical angles are congruent.
Point of intersection ‘P’ is the
common vertex of the four
angle.
𝐵
𝐴
𝐶
𝐷
𝑃
Common
Vertex
105º
105º
75º
75º

19.  1 &  4
Example 1:
1 2
3 4
5 6
7 8
 2 &  3
 5 &  8,
 6 &  7
Name the Vertical Angles
Vertical Angles

20. 145º
35º
𝑺𝒐𝒍𝒖𝒕𝒊𝒐𝒏:
2𝑥 + 3 = 105
2𝑥 = 105 − 3
2𝑥 = 102
2 2
𝒙 = 𝟓𝟏
𝟏𝟎𝟓°
Example :Given that the pair of angles are vertical angles. Find
for the angle measure and the value of the variable.
2) 105°
(2𝑥 + 3)°
1)
35°
145°
?
?
Vertical Angles
2𝑥 + 3; 𝑥 = 51
2 51 + 3 = 𝟏𝟎𝟓°

21. Complementary Angles
If the sum of two angles is 𝟗𝟎°, then they are called
complementary angles.
70º
20º
𝑋
𝑊 𝑌
𝑍
𝐴
60º
𝐵
𝐶
𝐸
30º
𝐹
𝐺
 ABC and EFG are
complementary angles.
𝒎𝑨𝑩𝑪 + 𝒎𝑬𝑭𝑮 = 𝟗𝟎°
60° + 30° = 90°
Not
adjacent
angles.
𝒎𝑾𝑿𝒀 + 𝒎𝒀𝑿𝒁 = 𝟗𝟎°
70° + 20° = 90°
𝑊𝑋𝑌 and YXZ are
complementary angles.
Adjacent
angles.

22. Example :Given that the pair of angles are complementary. Find
for the angle measure and the value of the variable.
Complement
16º
𝑺𝒐𝒍𝒖𝒕𝒊𝒐𝒏:
3𝑥 + 30 = 90
3𝑥 = 90 − 30
3𝑥 = 60
3 3
𝒙 = 𝟐𝟎
2)
(3𝑥)°
30°
𝟔𝟎°
1)
74º
?
Complementary Angles
3𝑥; 𝑥 = 20
3 20 = 𝟐𝟎°

23. Supplementary Angles
If the sum of two angles is 18𝟎°, then they are called
complementary angles.
𝐴
120º
𝐵 𝐶
𝐸
60º
𝐹 𝐺
 ABC and EFG are
supplementary angles.
𝒎𝑨𝑩𝑪 + 𝒎𝑬𝑭𝑮 = 𝟏𝟖𝟎°
120° + 60° = 180°

24. Linear Pair of Angles
Two angles are linear pair if they are adjacent and
supplementary.
55º
𝐴
125º
𝑃 𝐶
𝐷
 APC and APD are
supplementary angles
and are also adjacent
angles .
𝒎𝑨𝑷𝑪 + 𝒎𝑨𝑷𝑫 = 𝟏𝟖𝟎°
125° + 55° = 180°
Therefore,  APC and
APD are linear pair of
angles.

25. Supplementary & Linear Pair of Angles
1)
Supplement
37º
𝑺𝒐𝒍𝒖𝒕𝒊𝒐𝒏:
5𝑥 + 5 + 45 = 180
5𝑥 = 130
5𝑥 = 180 − 50
5 5
𝒙 = 𝟐𝟔
143º
?
𝟏𝟑𝟓°
Example :Given that the pair of angles are supplementary. Find
for the angle measure and the value of the variable.
5𝑥 + 50 = 180
2)
(5𝑥 + 5)°
45°
5𝑥 + 5; 𝑥 = 26
5 26 + 5 = 𝟏𝟑𝟓°

26. ACTIVITY

27. Activity 1: Angle Pairs
Direction: Identify the following pair of angles
35º
35º
1)
_____________________
2)
_____________________
125º
55º
3)
_____________________
43º 17º
4)
_____________________
Vertical Angles Linear Pair of Angles
Adjacent Angles Complementary Angles
3)
_____________________
Supplementary
Angles

28. Activity 2: Angle Pairs
Direction: Find the value of the missing angle.
102°
1) 2)
?
35º
4) 5)
3)
?
45°
35°
59°
?
?
102° 59°
?
18°
10°
85°
?
60°

29. Activity 3: Angle Pairs
Direction: Find the value of x.
(3𝑥 − 5)°
1) 2)
(2𝑥 − 6)°
3) 4)
𝑥°
𝑥°
40°
𝑥°
(3𝑥 + 16)°
60°
(2𝑥 + 8)° 36°
𝒙 = 𝟏𝟓
𝒙 = 𝟔𝟖
𝒙 = 𝟑𝟎 𝒙 = 𝟐𝟐

30. THANK YOU!
“The essence of Mathematics is
not to make simple things
complicated but to make
complicated things simple”
D.S Gudder