This document discusses elastic beam theory and how it relates to the bending of beams. It contains the following key points: 1) Elastic beam theory assumes the beam bends into a smooth curve such that cross-sections remain plane and perpendicular to the neutral axis. The radius of curvature is defined as the distance from the center of curvature to the beam. 2) Hooke's law and the flexure formula can be used to relate the radius of curvature to the internal moment and beam properties. Their product is called the flexural rigidity. 3) The moment-area theorems relate the slope and displacement of the beam to the area under the bending moment diagram divided by the flexural rigidity (M/

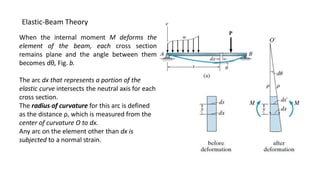
1. Elastic-Beam Theory
When the internal moment M deforms the
element of the beam, each cross section
remains plane and the angle between them
becomes dθ, Fig. b.
The arc dx that represents a portion of the
elastic curve intersects the neutral axis for each
cross section.
The radius of curvature for this arc is defined
as the distance ρ, which is measured from the
center of curvature O to dx.
Any arc on the element other than dx is
subjected to a normal strain.

2. Elastic-Beam Theory
For example, the strain in arc ds, located at a
position y from the neutral axis, is

3. If the material is homogeneous and behaves in a
linear elastic manner, then Hooke’s law applies,
Also, since the flexure formula applies,
Here
ρ = the radius of curvature at a specific point on the elastic
curve (1/ρ is referred to as the curvature)
M = the internal moment in the beam at the point where ρ is
to be determined
E = the material’s modulus of elasticity
I = the beam’s moment of inertia computed about the
neutral axis

4. The product EI in this equation is referred to as the
flexural rigidity, and it is always a positive quantity
Moment-Area Theorems
To develop the theorems, reference is made to the beam in Fig. a.
If we draw the moment diagram for the beam and then divide it
by the flexural rigidity, EI, the “M/EI diagram” shown in Fig.b
results.

5. Moment-Area Theorems
Thus it can be seen that the change dθ in the slope of the
tangents on either side of the element dx is equal to the
lighter-shaded area under the M/EI diagram.
Integrating from point A on the elastic curve to point B,
Fig. c, we have
This equation forms the basis for the first moment-area
theorem.
Theorem 1: The change in slope between any two
points on the elastic curve equals the area of the M/EI
diagram between these two points.

6. Theorem 1: The change in slope between any two
points on the elastic curve equals the area of the M/EI
diagram between these two points.
The notation θB/A is referred to as the angle of the
tangent at B measured with respect to the tangent at A,
Fig.c.
From the proof it should be evident that this angle is
measured counterclockwise from tangent A to tangent
B if the area of the M/EI diagram is positive,
Conversely, if this area is negative, or below the x axis,
the angle θ B/A is measured clockwise from tangent A to
tangent B.
Furthermore, θ B/A is measured in radians.

7. The second moment-area theorem is based on the
relative deviation of tangents to the elastic curve. Shown
in Fig.d is a greatly exaggerated view of the vertical
deviation dt of the tangents on each side of the
differential element dx.
This deviation is measured along a vertical line passing
through point A. Since the slope of the elastic curve and
its deflection are assumed to be very small, it is
satisfactory to approximate the length of each tangent
line by x and the arc ds by dt.
Using the circular-arc formula s = θr, where r is of length
x, we can write
dt = x dθ.
Using Eq.2, dθ = (M/EI) dx,
the vertical deviation of the tangent at A with respect to
the tangent at B can be found by integration, in which
case

8. Recall from statics that the centroid of an area is
determined from
Since represents an area of the M/EI
diagram, we can also write
Here x is the distance from the vertical axis through
A to the centroid of the area between A and B, Fig.
e.
Theorem 2: The vertical deviation of the
tangent at a point (A) on the elastic curve with
respect to the tangent extended from another
point (B) equals the “moment” of the area
under the M/EI diagram between the two
points (A and B). This moment is computed
about point A (the point on the elastic curve),
where the deviation t A/B is to be determined.

18. Conjugate-Beam Method
Here the shear V compares with the slope θ,
the moment M compares with the
displacement v,
and the external load w compares with the
M/EI diagram.
To make use of this comparison we will now
consider a beam having the same length as
the real beam, but referred to here as
the “conjugate beam,”
The conjugate beam is “loaded” with the
M/EI diagram derived from the load w on
the real beam.
From the above comparisons, we can state
two theorems related to the conjugate
beam, namely,

19. Theorem 1: The slope at a point in the real
beam is numerically equal to the shear at the
corresponding point in the conjugate beam.
Theorem 2: The displacement of a point in the
real beam is numerically equal to the moment
at the corresponding point in the conjugate
beam.

20. pin or roller support at the end of the real beam
provides zero displacement, but the beam has a
nonzero slope.
Consequently, from Theorems 1 and 2, the conjugate
beam must be supported by a pin or roller, since this
support has zero moment but has a shear or end
reaction.
When the real beam is fixed supported (3), both the
slope and displacement at the support are zero. Here
the conjugate beam has a free end, since at this end
there is zero shear and zero moment.
Corresponding real and conjugate-beam supports for
other cases are listed
in the table.