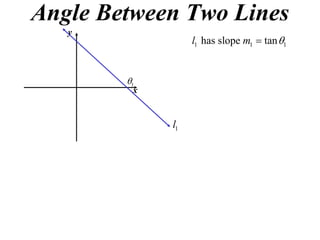
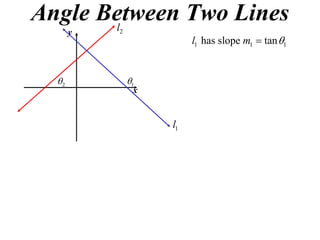
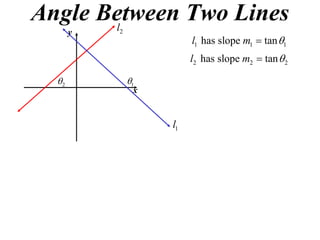
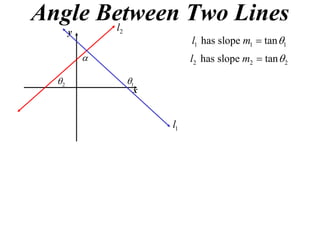
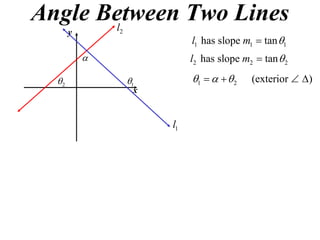
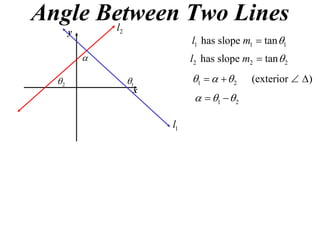
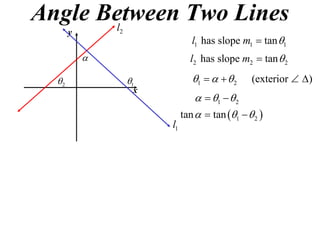
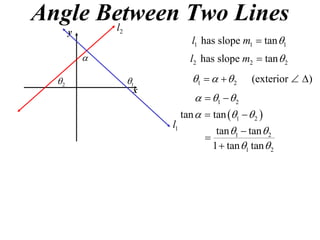
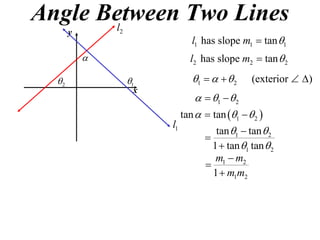
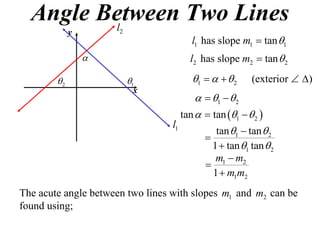
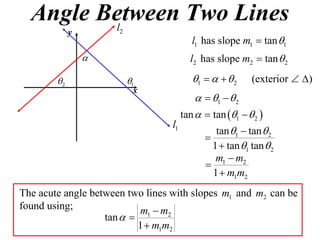
The document shows how to find the acute angle between two lines given their slopes. It provides examples that demonstrate using the formula tan(α) = (m1 - m2) / (1 + m1m2) to calculate the angle. For lines with slopes m1 and m2, this formula can be used to find the acute angle between them.

1. Angle Between Two Lines

2. Angle Between Two Lines
y
x

3. Angle Between Two Lines
y
1
x
l1

4. Angle Between Two Lines
y
l1 has slope m1  tan 1
1
x
l1

5. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
2 1
x
l1

6. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
l2 has slope m2  tan  2
2 1
x
l1

7. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1
x
l1

8. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
l1

9. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
  1   2
l1

10. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
  1   2
tan   tan 1   2 
l1

11. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
  1   2
tan   tan 1   2 
l1
tan 1  tan  2

1  tan 1 tan  2

12. Angle Between Two Lines
l
y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
  1   2
tan   tan 1   2 
l1
tan 1  tan  2

1  tan 1 tan  2
m1  m2

1  m1m2

13. Angle Between Two Lines
l y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
  1   2
tan   tan 1   2 
l1
tan 1  tan  2

1  tan 1 tan  2
m1  m2

1  m1m2
The acute angle between two lines with slopes m1 and m2 can be
found using;

14. Angle Between Two Lines
l y 2
l1 has slope m1  tan 1
 l2 has slope m2  tan  2
2 1 1     2 (exterior  )
x
  1   2
tan   tan 1   2 
l1
tan 1  tan  2

1  tan 1 tan  2
m1  m2

1  m1m2
The acute angle between two lines with slopes m1 and m2 can be
found using; m1  m2
tan  
1  m1m2

15. 2000 Extension 1 HSC Q1b)
e.g. Find the acute angle between the lines
1
y  2 x  1 and y  x  1
3

16. 2000 Extension 1 HSC Q1b)
e.g. Find the acute angle between the lines
1
y  2 x  1 and y  x  1
3
1
2
tan   3
1
1  2  
 3

17. 2000 Extension 1 HSC Q1b)
e.g. Find the acute angle between the lines
1
y  2 x  1 and y  x  1
3
1
2
tan   3
1
1  2  
 3
6 1

3 2

18. 2000 Extension 1 HSC Q1b)
e.g. Find the acute angle between the lines
1
y  2 x  1 and y  x  1
3
1
2
tan   3
1
1  2  
 3
6 1

3 2
1

19. 2000 Extension 1 HSC Q1b)
e.g. Find the acute angle between the lines
1
y  2 x  1 and y  x  1
3
1
2
tan   3
1
1  2  
 3
6 1

3 2
1
  45

20. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.

21. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m

22. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m

23. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m

24. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m

25. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m
4m  2

26. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m
4m  2
1
m
2

27. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m
4m  2  1  3m  3  m
1
m
2

28. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m
4m  2  1  3m  3  m
1
m 2m  4
2

29. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m
4m  2  1  3m  3  m
1
m 2m  4
2
m  2

30. 2005 Extension 1 HSC Q1f)
(ii) The acute angle between the lines y = 3x + 5 and y = mx + 4 is 45
Find the possible values of m.
3 m
tan 45 

1  3m
3 m
1
1  3m
1  3m  3  m
1  3m  3  m or  1  3m   3  m
4m  2  1  3m  3  m
1
m 2m  4
2
1 m  2
 m  or m  2
2

31. Exercise 14E; 1ac, 2bdf, 4, 7, 8, 10, 11a, 15*