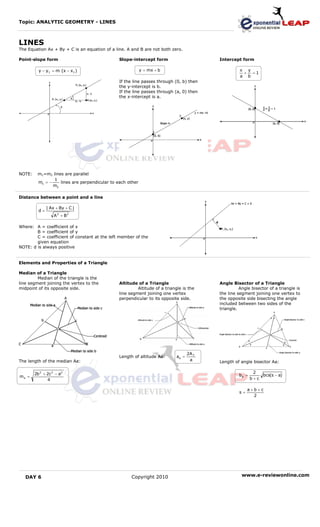
This document discusses fundamental concepts in analytic geometry related to lines. It defines key terms like slope, the different forms of a line equation, and how to find the distance from a point to a line. It also covers properties and elements of triangles, including how to calculate the length of a median, altitude, and angle bisector.

1. Topic: ANALYTIC GEOMETRY - LINES
FUNDAMENTALS
RECTANGULAR OR CARTESIAN COORDINATES
Division of Line Segment
x1 + x 2
The x-coordinate is the abscissa, and the y-coordinate is the x=
2
ordinate.
Distance between two points y1 + y 2
y=
2
Slope and Inclination of a Line
The slope (m) of a line is the tangent of the inclination
2 2
The distance between P1 and P2: d = (x 2 − x1 ) + (y2 − y1 )
m = tan θ
Area of a Triangle Let P1 (x1, y1) and P2 (x2, y2) be two given points, and is
indicated by slope m
1 x1 x 2 x 3
A= y 2 − y1
2 y1 y 2 y 3 m = tan θ =
x 2 − x1
1
A = [(x1y2 + x 2 y3 + x3y1 ) − (y1x2 + y 2 x3 + y 3x1 )] Angle between Two Lines
2
Area of polygon of n-sides
1 x1 x2 x3 ... xn
A =
2 y1 y2 y3 ... yn
m2 − m1
tan θ =
1 + m2m1
Where: m1 = slope of line 1
m2 = slope of line 2
θ = angle from line 1 to line 2, measured
clockwise from line 1 to line 2
DAY 6 Copyright 2010 www.e-reviewonline.com

2. Topic: ANALYTIC GEOMETRY - LINES
LINES
The Equation Ax + By + C is an equation of a line. A and B are not both zero.
Point-slope form Slope-intercept form Intercept form
y − y1 = m (x − x1 ) y = mx + b x y
+ =1
a b
If the line passes through (0, b) then
the y-intercept is b.
If the line passes through (a, 0) then
the x-intercept is a.
NOTE: m1=m2 lines are parallel
1
m1 = − lines are perpendicular to each other
m2
Distance between a point and a line
| Ax + By + C |
d=
A 2 + B2
Where: A = coefficient of x
B = coefficient of y
C = coefficient of constant at the left member of the
given equation
NOTE: d is always positive
Elements and Properties of a Triangle
Median of a Triangle
Median of the triangle is the
line segment joining the vertex to the Altitude of a Triangle Angle Bisector of a Triangle
midpoint of its opposite side. Altitude of a triangle is the Angle bisector of a triangle is
line segment joining one vertex the line segment joining one vertex to
perpendicular to its opposite side. the opposite side bisecting the angle
included between two sides of the
triangle.
2A T
Length of altitude Aa: aa =
The length of the median Aa: a Length of angle bisector Aa:
2b 2 + 2c 2 − a2 2
ma = ba = bcs(s − a)
4 b+c
a+b+c
s=
2
DAY 6 Copyright 2010 www.e-reviewonline.com