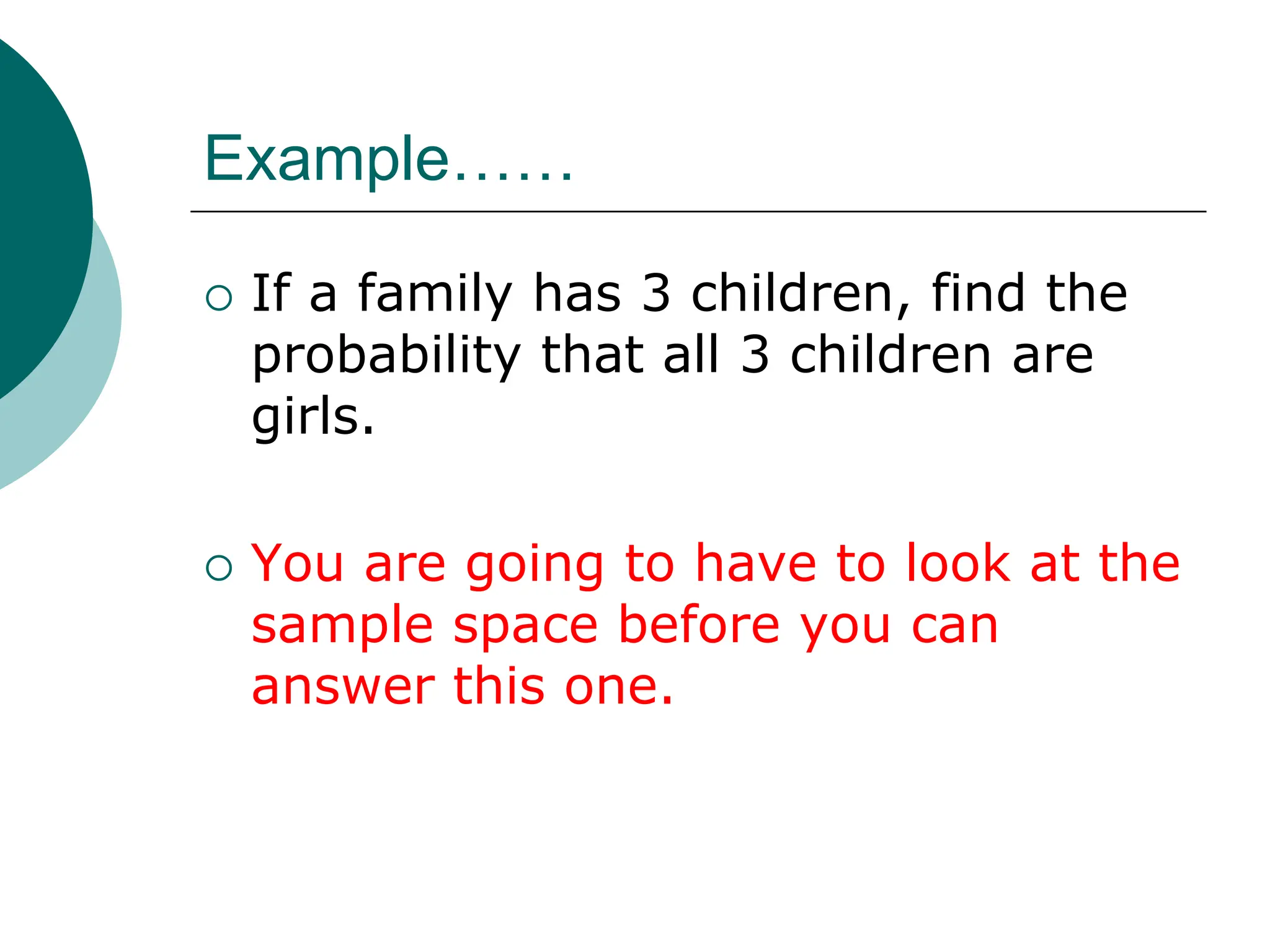
This document discusses probability and sample spaces. It defines key probability terms like probability experiment, outcome, and sample space. It provides examples of finding the sample space for experiments like tossing a coin or die. The document also discusses different methods for calculating probability, including empirical, theoretical, and subjective probabilities. It introduces concepts like the law of large numbers and probability rules. Examples are provided for finding probabilities of events occurring as well as complementary events.

1. Probability and Sample
Space…….

2. Vocabulary To Know
 Probability Experiment: A
chance process that leads to well
defined results called outcomes.
 Outcome: The result of a single
trial of a probability experiment.

3. Sample Space
 Sample Space:
the set of ALL
possible outcomes
of a probability
experiment.
 Example:
 Flipping a coin
has 2 possible
outcomes
1. Heads
2. Tails

4. You Try
 Find the sample space for the
following probability experiments.
1. Toss One Coin
2. Roll a Die
3. Answer a T/F Question
4. Toss 2 Coins

5. Answers
1. Toss One Coin
2. Roll a Die
3. Answer T/F
Question
4. Toss 2 Coins
1. H,T
2. 1,2,3,4,5,6
3. T,F
4. HH, TT, HT, TH

6. Finding a Probability
 The probability of an event can be
obtained by 3 different methods:
1. Empirical - experimental
2. Theoretical – assumes all outcomes in
the sample space are equally likely to
occur.
3. Subjective – a value based on an
educated guess.

7. Empirical Probability
trials
of
occurred
A
times
of
n
A
n
A
P
#
#
)
(
)
(
'



8. Empirical Probability Example
 If a person rolls a
die 40 times and 9
of the rolls results
in a “5”, what
empirical
probability was
observed for the
event “5”?
 Answer:
225
.
40
9
)
5
(
'


P

9. Theoretical Probability
space
sample
in
outcomes
total
E
event
in
outcomes
of
E
P
#
)
( 

10. Theoretical Probability Example
 What is the
probability of
rolling a die and
getting a “5”?
 Answer:
17
.
6
1
)
( 

E
P

11.  The difference between theoretical
and empirical probability is that
theoretical assumes that certain
outcomes are equally likely while
empirical probability relies on actual
experience to determine the
likelihood of outcomes.

12. Law of Large Numbers
 The Law of Large Numbers says
that as the # of trials in an
experiment increases, the empirical
probability approaches the
theoretical probability.
 If an experiment is done many
times, everything tends to “even
out.”

13. Labs
Let’s try to see how the Law of
Large Numbers works……..

14. Theoretical Probability…..

15. How are probabilities expressed?
 Probabilities are
expressed as
reduced fractions,
decimals rounded
to 2 or 3 decimal
places, or, where
appropriate,
percentages
 Examples:
1.
2. 0.5
3. 50%
2
1

16. Example……
 Find the
probability of
drawing a queen
from a deck of
cards.
 Answer:
13
1
52
4
)
( 

Queen
P

17. Example……
 If a family has 3 children, find the
probability that all 3 children are
girls.
 You are going to have to look at the
sample space before you can
answer this one.

18. Looking for all 3 girls……
 Sample Space:
BBB
BBG
BGB
GBB
GGG
GGB
GBG
BGG
 Answer:
8
1
)
3
( 
Girls
All
P

19. Example……
 A card is drawn from an ordinary
deck. Find these probabilities:
a. P(Jack)
b. P(6 of Clubs)
c. P(Red Queen)

20. Answers……
a.
b.
c.
13
1
52
4
)
( 

Jack
P
52
1
)
6
( 
CLUBS
OF
P
26
1
52
2
)
( 

QUEEN
RED
P

21. Probability Rules……
 Rule 1:
The probability of
an event is
between 0 and 1.
 In other words….
*The probability
can NOT be
negative.
*The probability
can NOT be
greater than 1.
1
)
(
0 
 A
P

22.  Rule 2:
If an event can
NOT occur, then
the probability is
0.
 Example:
Find the P(9) on a
die.
 Answer:
P(9) = 0

23.  Rule 3:
If an event is
certain, then the
probability is 1.
 Example:
Roll a die. What is
the probability of
getting a number
less than 7?
 Answer:
P(# less than 7) =
1

24.  Rule 4:
The sum of the
probabilities in the
sample space is 1.
 Example:
In a roll of a die,
each outcome in
the sample space
has a probability
of 1/6. See chart.
x 1 2 3 4 5 6
P(x) 1/6 1/6 1/6 1/6 1/6 1/6
6/6
= 1

25. Complement……
 The complement is the set of all
outcomes in the sample space that
are NOT included in the event, A.
 In other words, it is the probability
of event NOT occurring.
)
(
1
)
( A
P
A
P 


26. Example……
 Find the
complement of
getting an odd #
on the roll of a die.
 Answer:
Getting an EVEN
number.

27. Example……
 If the probability
that a person
owns a computer
is 0.70, find the
probability that a
person does not
own a computer.
 Answer:
P(Not Owning) =
1 -.70
P(Not Owning) = .30

28. Example……
 If the probability
that a person does
not own a TV is
1/5, find the
probability that a
person does own
a TV.
 Answer:
P(Does) = 1 – 1/5
P(Does) = 4/5

29. Example……
 2 dice are rolled. Find
a. P(sum of 3)
b. P(at least 3)
c. P(more than 9)

30. You need your array of the sums
first……
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12

31. P(sum of 3)
 Answer:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
18
1
36
2
)
3
( 

of
sum
P

32. P(at least 3) - Use the
complement……
 Answer:
 Prob = 1 – 1/36 =
35/36
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
)
3
(
1
)
3
( than
less
P
least
at
P 


33. P(more than 9)……
 Answer:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
6
1
36
6
)
9
( 

than
more
P