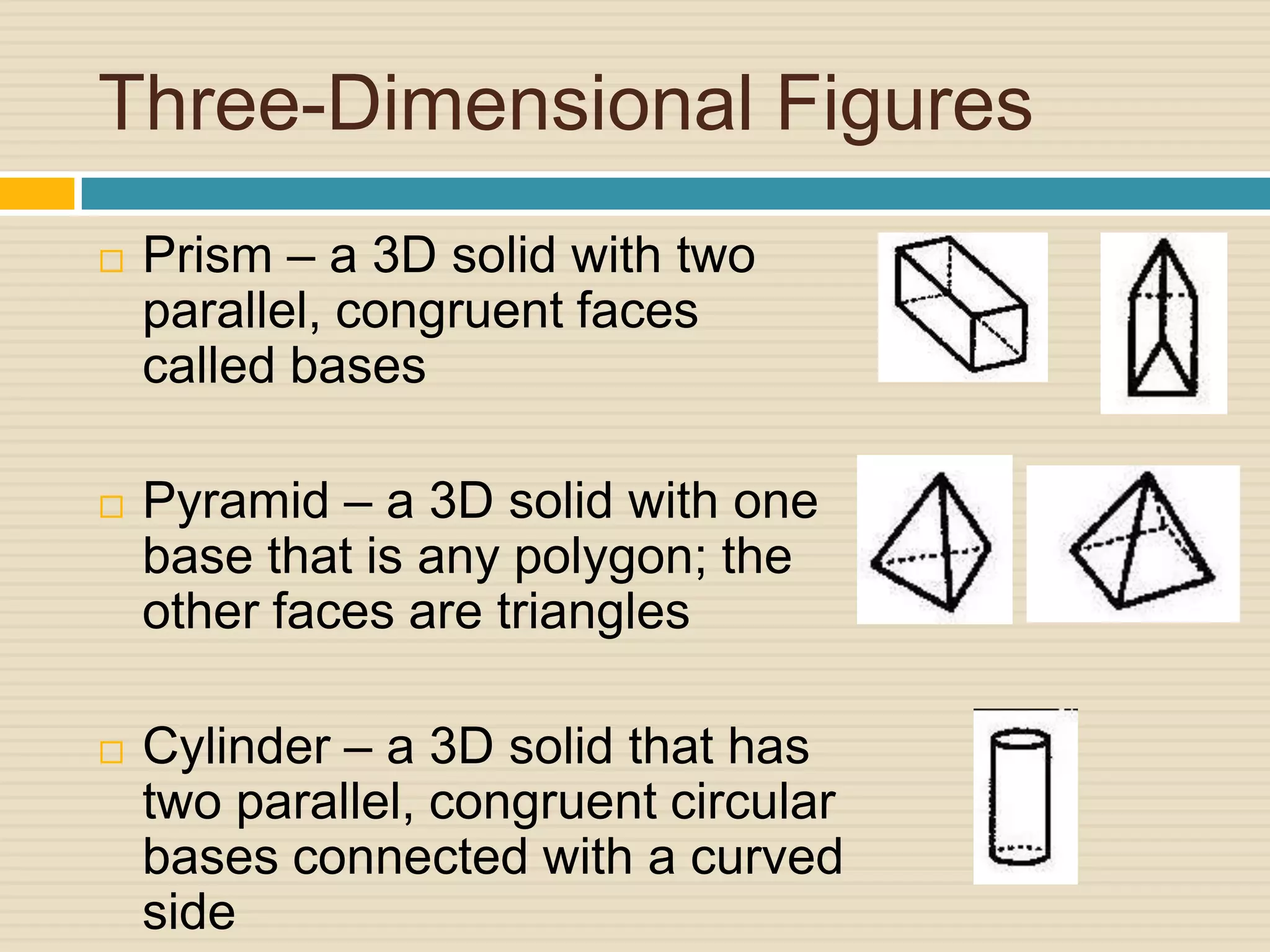
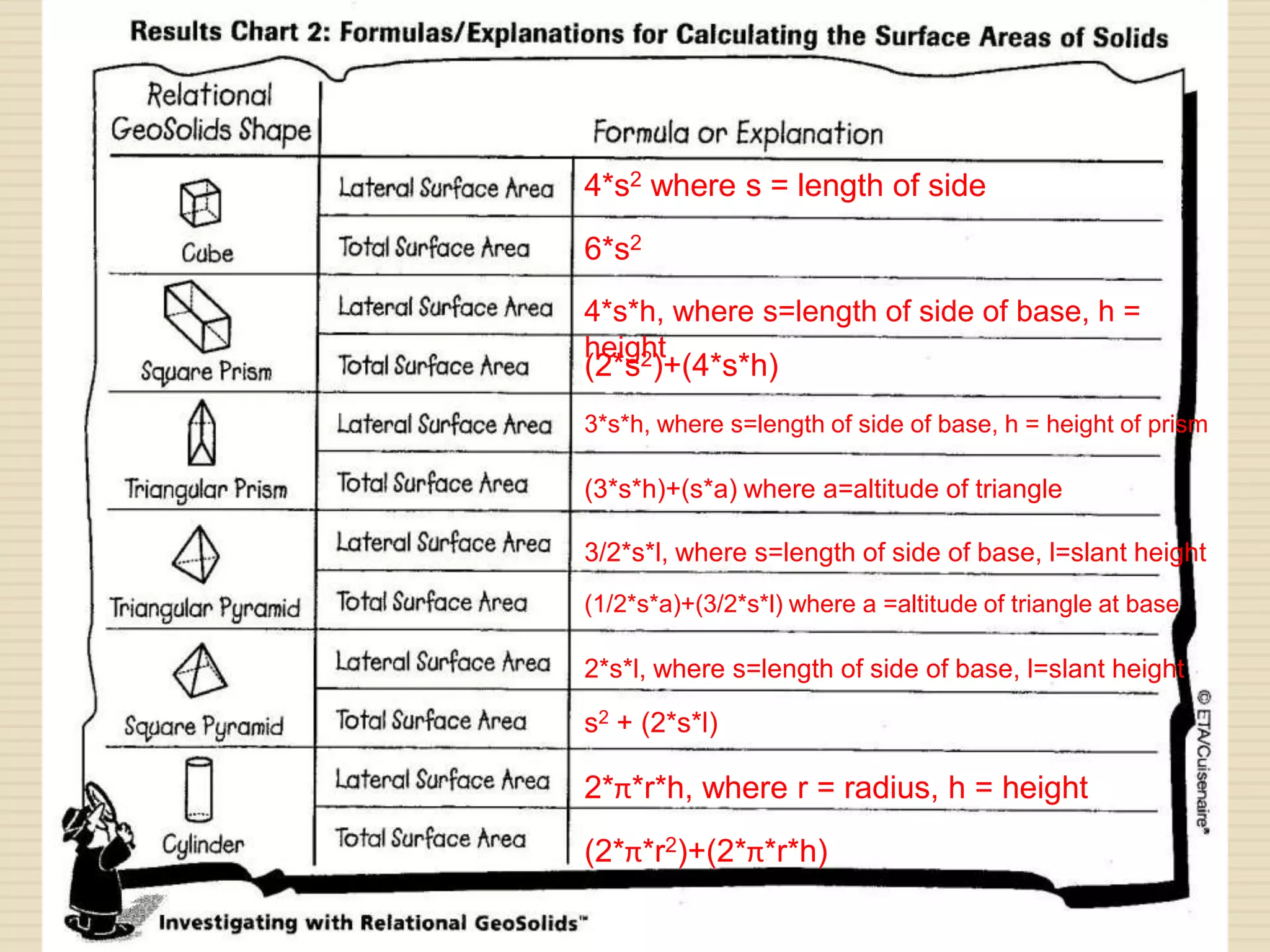
The document discusses surface area of three-dimensional geometric solids including prisms, pyramids, and cylinders. It defines surface area as the sum of the areas of all surfaces, and lateral surface area as excluding the base(s). Formulas are provided to calculate the surface area of various solids using measurements like side length, height, radius, and slant height.

1. Surface Area of SolidsMarch 22, 2010

2. Three-Dimensional FiguresPrism – a 3D solid with two parallel, congruent faces called basesPyramid –a 3D solid with one base that is any polygon; the other faces are trianglesCylinder – a 3D solid that has two parallel, congruent circular bases connected with a curved side

3. Surface AreaSurface area refers to the sum of the areas of all the surfaces of a 3D figure. Also called Total Surface Area (TSA)Examples: wrapping paperorange

4. Lateral Surface AreaLateral surface area of a solid only includes the faces or surfaces that make up the sides of the solid (not the base(s))Examples: Soup can label

5. With a partner, you will determine the surface area of various geometric solids. How Do You Find the Surface Area of a Solid?

6. 4*s2 where s = length of side6*s24*s*h, where s=length of side of base, h = height(2*s2)+(4*s*h)3*s*h, where s=length of side of base, h = height of prism(3*s*h)+(s*a) where a=altitude of triangle3/2*s*l, where s=length of side of base, l=slant height(1/2*s*a)+(3/2*s*l) where a =altitude of triangle at base2*s*l, where s=length of side of base, l=slant heights2 + (2*s*l)2*π*r*h, where r = radius, h = height(2*π*r2)+(2*π*r*h)