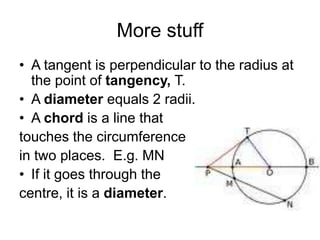
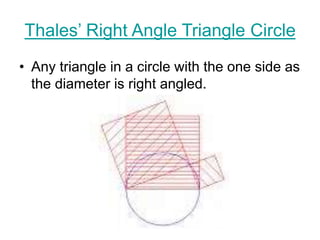
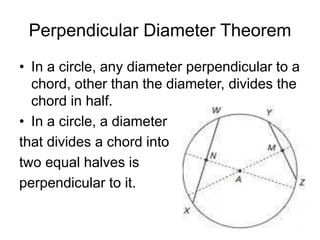
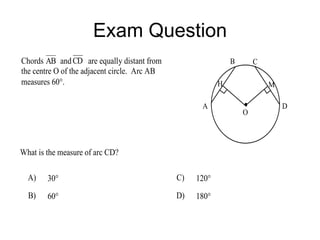
This document discusses circle theorems and identities. It begins by outlining what will be covered, including determining lengths and segments in circles, arcs of circles, and angles in circles. It then reviews basic properties like all radii of a given circle being congruent and definitions of tangents, secants, and disjoint lines. The document continues to define properties of tangents, diameters, chords, and right triangles formed with the diameter. It concludes with additional circle theorems and sample exam questions testing these concepts.

1. Circle Theorem
Circle Identities

2. What will we do?
• We will learn how to determine:
• Lengths and segments in circles
• Arcs of circles
• Angles in the circle
• Distances in a circle

3. Stuff you know…
• What follows are rules ‘n stuff you
probably already know, so we don’t need
to go into that in great depth.
• All radii of a given circle are congruent.
• A tangent is a line that hits a circle once.
• A secant is a line that hits a circle twice.
• When a line does not hit a circle, they are
said to be disjoint.

4. More stuff
• A tangent is perpendicular to the radius at
the point of tangency, T.
• A diameter equals 2 radii.
• A chord is a line that
touches the circumference
in two places. E.g. MN
• If it goes through the
centre, it is a diameter.

5. Thales’ Right Angle Triangle Circle
• Any triangle in a circle with the one side as
the diameter is right angled.

6. Perpendicular Diameter Theorem
• In a circle, any diameter perpendicular to a
chord, other than the diameter, divides the
chord in half.
• In a circle, a diameter
that divides a chord into
two equal halves is
perpendicular to it.

7. More rules…
• In a circle, two congruent chords are
equidistant from the centre.
• In a circle, two chords that are equidistant
from the centre are congruent.
• In a circle, two congruent
chords intercept equal arcs.

8. Exam Question
•
In the circle with centre O illustrated below,
.EFHOandDCGO 
A
B
C
D
E
F
G
H
O
Which of the following statements is always true?
A) m DGC = m EHF C)
m BO m AO
B) m DG = m EH D) m DA
m DC

2

9. Exam Question
In an equilateral triangle ABC inscribed in a circle with
centre O, radius OE is drawn perpendicular to segment BC.
B
A C
E
O
Which of the following statements justifies that arc BE is congruent to arc EC?
A) A radius that is perpendicular to a chord bisects that chord.
B) In a circle, congruent chords are equidistant from the centre.
C) The inscribed angles A, B and C are congruent because the angles of an equilateral
triangle are congruent.
D) A radius that is perpendicular to a chord bisects the arc subtended by that chord.

10. Exam Question
Chords AB andCD are equally distant from
the centre O of the adjacent circle. Arc AB
measures 60.
A
B C
D
H M
O
What is the measure of arc CD?
A) 30 C) 120
B) 60 D) 180

11. Exam QuestionGiven the information provided for each diagram below, in which one of these circles
would chord PQ have to be a diameter?
A) PR  QS
S
Q
P
R
C) RSPQandMSRM 
S
Q
P
R
M
B) RQPR 
Q
P
R
D) RS//PQ
S
Q
P
R

12. Activity
• Page 293, Q. 8, 15, 16, 17, 20