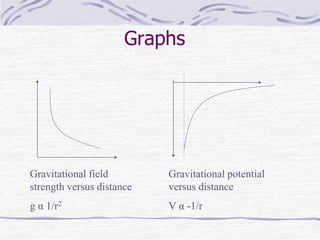
1) Gravitational and electric fields can be described by their field strength, which is defined as the force exerted per unit mass or charge. 2) Gravitational field strength is calculated using Newton's law of universal gravitation, while electric field strength uses Coulomb's law. 3) The electric potential at a point is defined as the work required to move a unit charge from infinity to that point, and equipotentials are surfaces or lines of constant potential.

1. Topic 10
Topic 10.1 Describing fields

2. When forces act at a distance, physicists
use the notion of a field to explain this.
How can you describe a field?
What produces fields?

3. GRAVITATIONAL
FIELDS

4. Gravitational Field Strength
A mass M creates a gravitational field in
space around it.
If a mass m is placed at some point in
space around the mass M it will
experience the existance of the field in
the form of a gravitational force
Recap

5. We define the gravitational field strength
as the ratio of the force the mass m
would experience to the mass, m
That is the gravitational field strength at a
point, it is the force exerted per unit mass
on a particle of small mass placed at that
point
Recap

6. The force experienced by a mass m
placed a distance r from a mass M is
F = G Mm
r2
And so the gravitational field strength of
the mass M is
g = G M
r2
Recap

7. The units of gravitational field strength are
N kg-1
The gravitational field strength is a vector
quantity whose direction is given by the
direction of the force a mass would
experience if placed at the point of interest
Recap

8. Field Strength at the Surface
of a Planet
If we replace the particle M with a sphere
of mass M and radius R then relying on the
fact that the sphere behaves as a point
mass situated at its centre the field strength
at the surface of the sphere will be given by
g = G M
R2
Recap

9. If the sphere is the Earth then we have
g = G Me
Re
2
But the field strength is equal to the acceleration
that is produced on the mass, hence we have that
the acceleration of free fall at the surface of the
Earth, g
g = G Me
Re
2
Recap

10. Gravitational Energy
and Potential
We know that the gravitational potential energy
increases as a mass is raised above the Earth
The work done in moving a mass between two
points is positive when moving away from the
Earth
By definition the gravitational potential energy
is taken as being zero at infinity
It is a scalar quantity

11. The gravitational potential at any point in the
Earth´s field is given by the formula
V = - G Me
r
Where r is the distance from the centre of the
Earth (providing r >R)
The negative sign allows for the fact that all the
potentials are negative as they have to increase
to zero

12. Definition
The potential is therefore a measure of the
amount of work that has to be done to move
particles between points in a gravitational field
and its units are J kg –1
The work done is independent of the path
taken between the two points in the field, as it
is the difference between the initial and final
potentials that give the value

13. Graphs
Gravitational field
strength versus distance
g α 1/r2
Gravitational potential
versus distance
V α -1/r

14. ELECTROSTATIC
FIELDS

15. If a very small, positive point charge
Q, the test charge, is placed at any
point in an electric field and it
experiences a force F, then the field
strength E (also called the E-field) at
that point is defined by the equation
𝐸 =
𝐹
𝑞
Recap

16. The magnitude of E is the force per unit charge
and its direction is that of F (i.e. of the force
which acts on a positive charge).
If F is in newtons (N) and Q is in coulombs (C)
then the unit of E is the newton per coulomb (N
C-1).
Recap

17. Coulomb’s Law
Coulomb’s law states that the force acting
between two charges q1 and q2 whose
distances are separated by a distance d is
directly proportional to the product of the
charges and inversely proportional to the
square of the distance between them.
The force is along the line joining the
centres of the charges.
Recap

18. Coulomb’s Law
𝑭 =
𝟏
𝟒𝝅𝜺𝜺 𝒐
𝒒 𝟏 𝒒 𝟐
𝒓 𝟐
Recap

19. Electric Potential due to a
Point Charge
The electric potential at a point in an electric
field is defined as being numerically equal to
the work done in bringing a unit positive charge
from infinity to the point.
Electric potential is a scalar quantity and it
has the volt V as its unit.
Based on this definition, the potential at
infinity is zero.

20. Let us take a point r metres from a charged object.
The potential at this point can be calculated using
the following

21. Electric Field Strength and Potential
Suppose that the
charge +q is moved
a small distance by
a force F from A to
B so that the force
can be considered
constant.

22. The work done is given by:
ΔW = Fx Δx
The force F and the electric field E are
oppositely directed, and we know that:
F = -q x E
Therefore, the work done can be given
as:
ΔW = -qE x Δ x = qV

23. Therefore E = - ΔV / Δx
This is the potential gradient.

24. Electric Field and Potential due to
a charged sphere

25. When the sphere becomes charged, we know that the
charge distributes itself evenly over the surface.
Therefore every part of the material of the conductor is at
the same potential.
As the electric potential at a point is defined as being
numerically equal to the work done in bringing a unit
positive charge from infinity to that point, it has a
constant value in every part of the material of the
conductor,

26. Since the potential is the same at all points on the
conducting surface, then Δ V / Δx is zero. But E = - Δ V /
Δ x.
Therefore, the electric field inside the conductor is zero.
There is no electric field inside the conductor.

27. Equipotentials
Regions in space where the electric potential
of a charge distribution has a constant value
are called equipotentials.
The places where the potential is constant in
three dimensions are called equipotential
surfaces, and where they are constant in
two dimensions they are called
equipotential lines.

28. They are in some ways analogous to the contour
lines on topographic maps. Similar also to
gravitational potential.
In this case, the gravitational potential energy is
constant as a mass moves around the contour
lines because the mass remains at the same
elevation above the earth's surface.
The gravitational field strength acts in a direction
perpendicular to a contour line.

29. Similarly, because the electric potential on an
equipotential line has the same value, no work
can be done by an electric force when a test
charge moves on an equipotential.
Therefore, the electric field cannot have a
component along an equipotential, and thus it
must be everywhere perpendicular to the
equipotential surface or equipotential line.
This fact makes it easy to plot equipotentials if the
lines of force or lines of electric flux of an electric
field are known.

30. In this image the lines are equally
spaced…it is a uniform field
In the real world the lines are surfaces,
but we cant show that on paper very well

31. Equipotentials for 2 point masses
is like two positive charges

32. For example, there are a series of equipotential
lines between two parallel plate conductors that
are perpendicular to the electric field.
There will be a series of concentric circles that
map out the equipotentials around an isolated
positive sphere.
The lines of force and some equipotential lines
for an isolated positive sphere are shown in the
next figures.