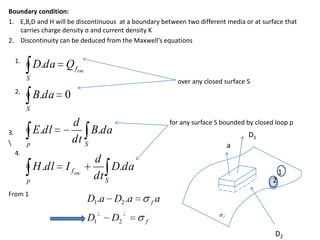
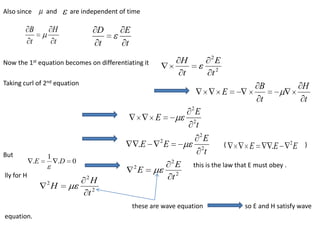
Maxwell's equations govern electric and magnetic fields and describe how they change over time. The equations relate the electric field, magnetic field, electric displacement field, magnetic induction, electric charge density, and electric current density. Maxwell showed that changing electric fields produce magnetic fields and changing magnetic fields produce electric fields. This led to the prediction and understanding of electromagnetic waves, including light. The equations also describe conditions at boundaries between different media, where some field components are continuous while others experience a discontinuity.

1. Maxwell’s EquationsPresented by :Anup Kr BordoloiECE Department ,Tezpur University09-18-2008

2. ContentsField equations

3. Equation of continuity for time varying fields

4. Inconsistency of Ampere’s Law

5. Maxwell’s equations

6. Conditions at a Boundary surfacesThe equations governing electric field due to charges at rest and the static magnetic field due to steady currents areContained in the above is the equation of continuity Time Varying Fields:From Faraday’s LawIn time varying electric and magnetic fields path of integration can be considered fixed. Faraday’s Law becomes Hence 1st equation becomes

7. Equation of continuity for Time-Varying Fields:From conservation of charge concept if the region is stationaryDivergence theorem time varying form of equation of Continuity Inconsistency of Ampere’s Law:Taking divergence of Ampere’s law hence Ampere’s law is not consistent for time varying equation of continuity. (from Gauss’s Law) displacement current density.

8. Hence Ampere’s law becomes .Now taking divergence results equation of continuityIntegrating over surface and applying Stokes’s theorem magneto motive force around a closed path=total current enclosed by the path.Maxwell’s equations: These are electromagnetic equations .one form may be derived from the other with the help of Stokes’ theorem or thedivergence theorem Contained in the above is the equation of continuity.

9. Word statement of field equation:1.The magneto motive force (magnetic voltage)around a closed path is equal to the conduction currentplus the time derivative of electric displacement through any surface bounded by the path.2.The electromotive force (electric voltage)around a closed path is equal to the time derivative of magnetic displacement through any surface bounded by the path3.Total electric displacement through the surface enclosing a volume is equal to the total charge wihin the volume.4.The net magnetic flux emerging through any closed surface is zero. Interpretation of field equation:Using Stokes’ theorem to Maxwell’s 2nd equationAgain from Faraday’s law region where there is no time varying magnetic flux ,voltagearound the loop would be zero the field is electrostatic and irrational.Again there are no isolated magnetic poles or “magnetic charges” on which lines of magnetic flux can terminate(the lines of mag.flux are continuous)

10. Boundary condition:1. E,B,D and H will be discontinuous at a boundary between two different media or at surface that carries charge density σ and current density KDiscontinuity can be deduced from the Maxwell’s equations 1. over any closed surface S 2. for any surface S bounded by closed loop p3.\ 4.From 1 D1a12D2

11. The component of D that is perpendicular to the interface is discontinuous by an amountlly from equation 2From equation 3 If width of the loop goes to zero,the flux vanishes. E parallel to the interface is continuous.From equation 4 Current passing through the amperian loop ,No volume current density will continue, but a surface current can.But 1l2

12. In case of linear media aboveboundary conditions can be written as if there is no free charge or free current at the interface

13. Condition at boundary surfaces:Space derivative can’t yield information about the points of discontinuity in the medium. integral form can do the task.From Maxwell’s 2nd equationFrom the fig.Area of the rectangle is made to approach to zero reducing it’s width yx

14. Tangential component of E is continuous.lly tangential component of H is continuous(for finite current density)Condition for normal component of B and D:Integral form of 3rd equationFor elementary pillbox for the case of no surface charge For metallic surface if surface charge density the charge density of surface layer is

15. For metallic conductor it is zero for electrostatic case or in the case of a perfect conductor normal component of the displacement density of dielectric =surface charge density of on the conductor.Similar analysis leads for magnetic field

16. Electromagnetic Waves in homogeneous medium:The following field equation must be satisfied for solution of electromagnetic problem there are three constitutional relation which determines characteristic of the medium in which the fields exists.Solution for free space condition:in particular case of e.m. phenomena in free space or in a perfect dielectric containing no charge and no conduction currentDifferentiating 1st

17. Also since and are independent of time Now the 1st equation becomes on differentiating itTaking curl of 2nd equation ( )But this is the law that E must obey .lly for H these are wave equation so E and H satisfy wave equation.