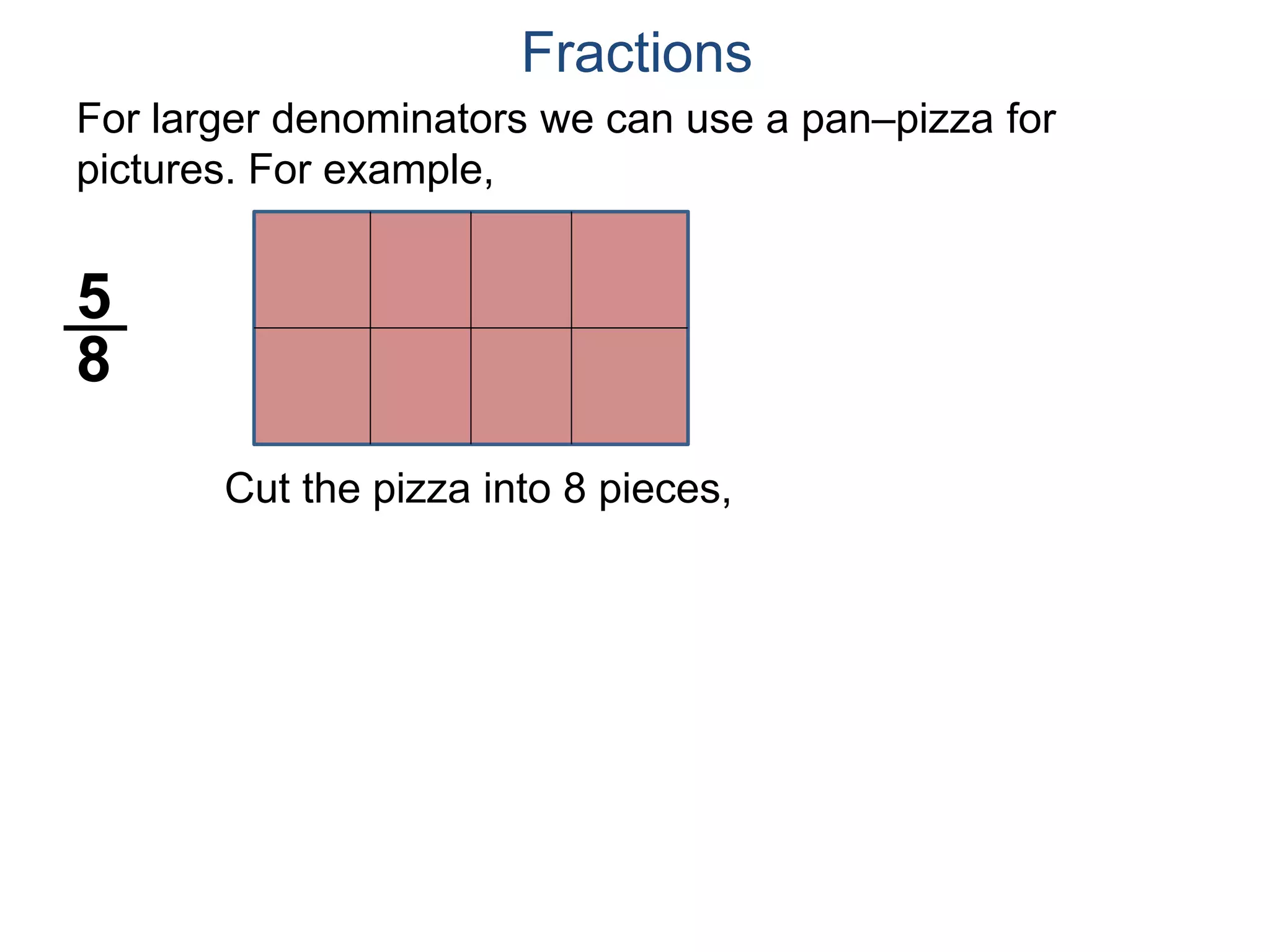
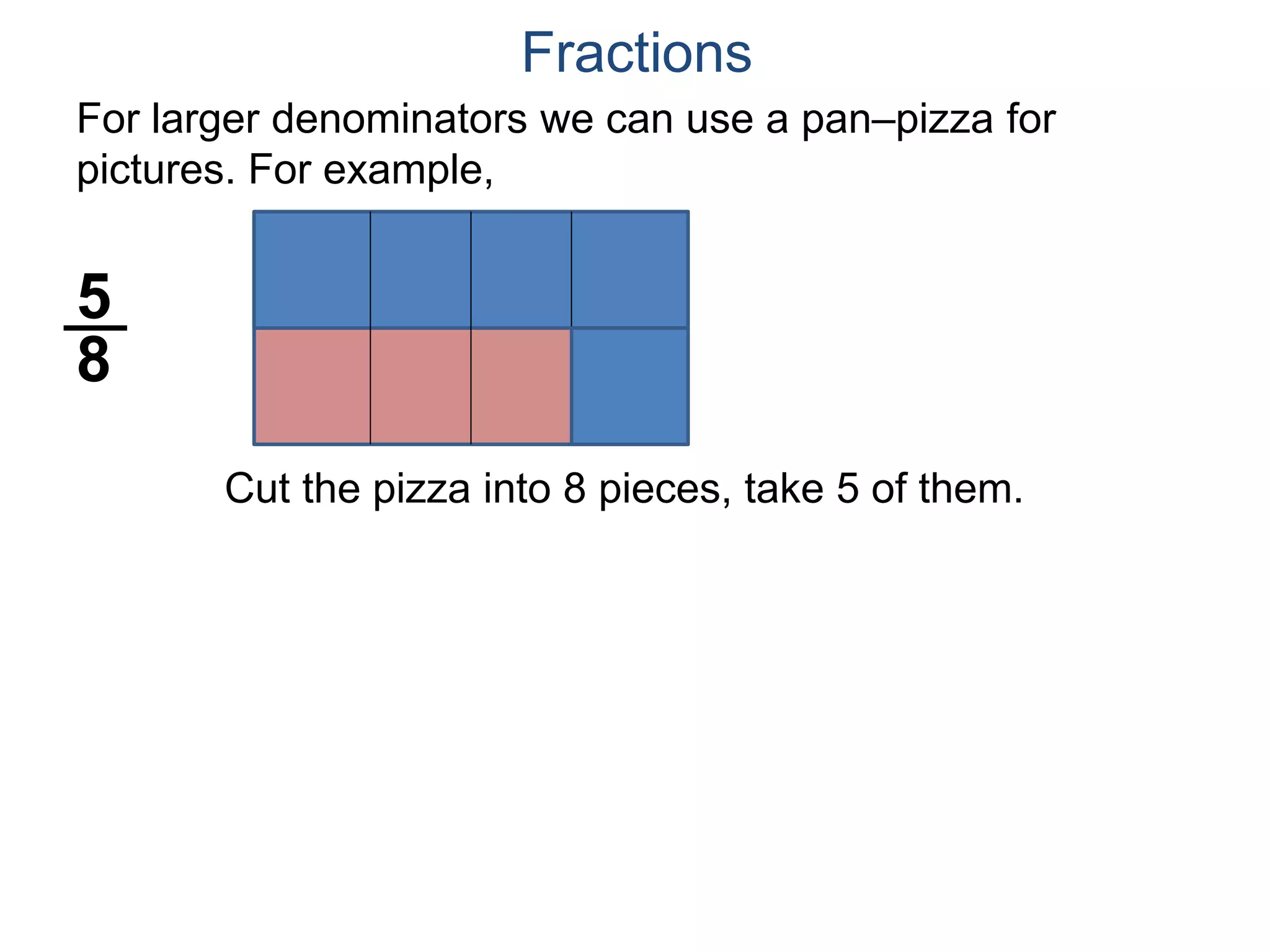
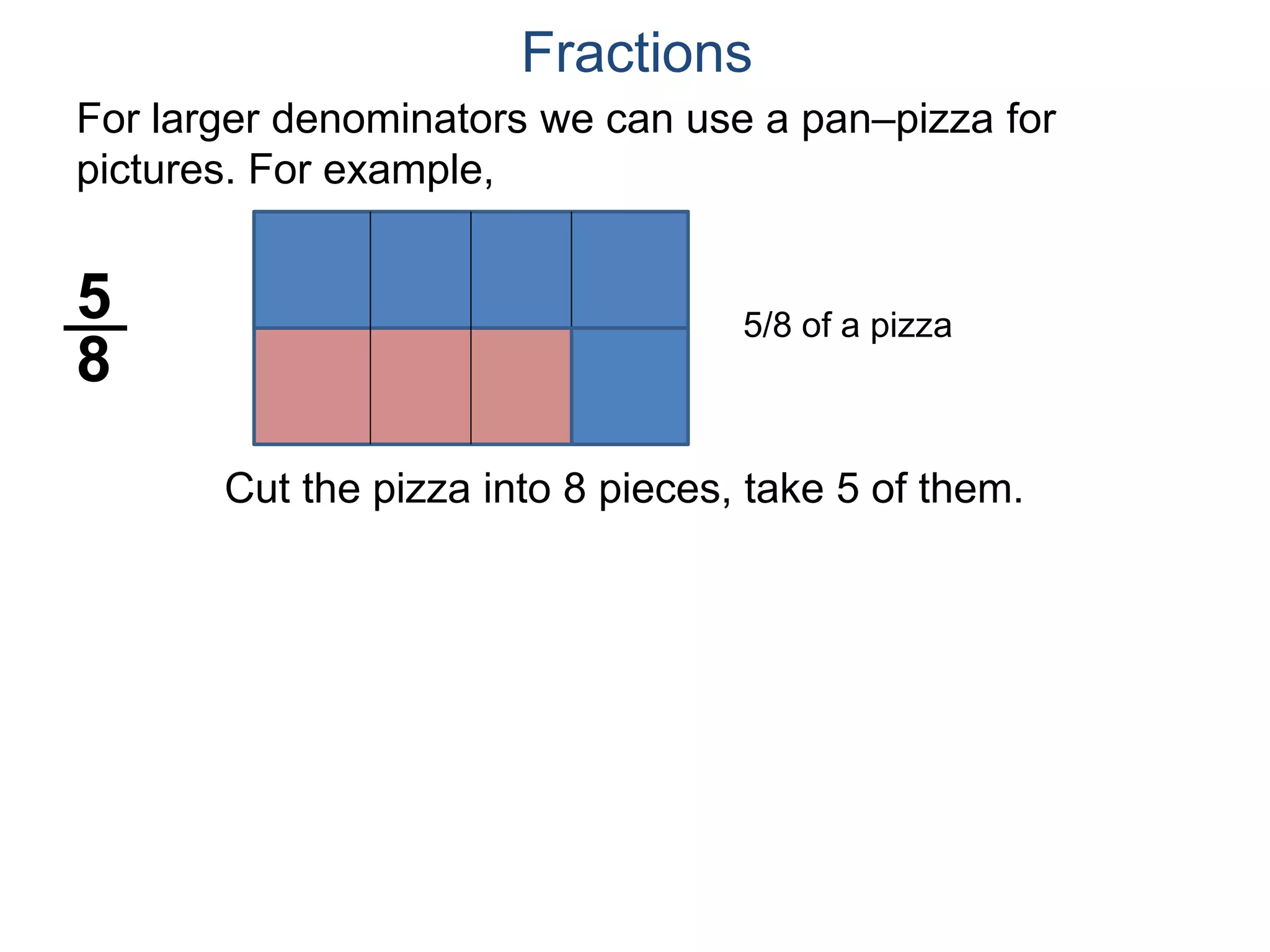
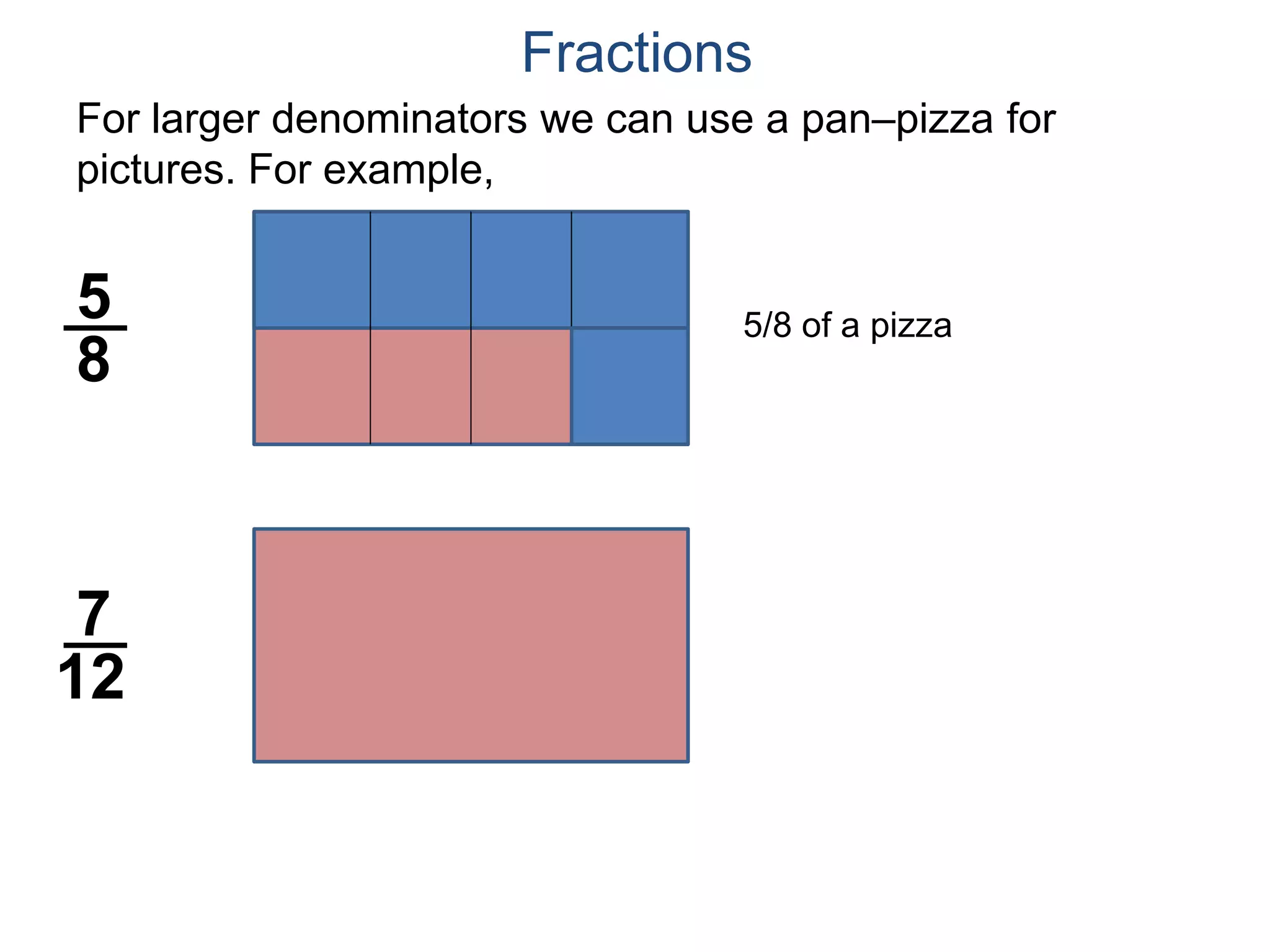
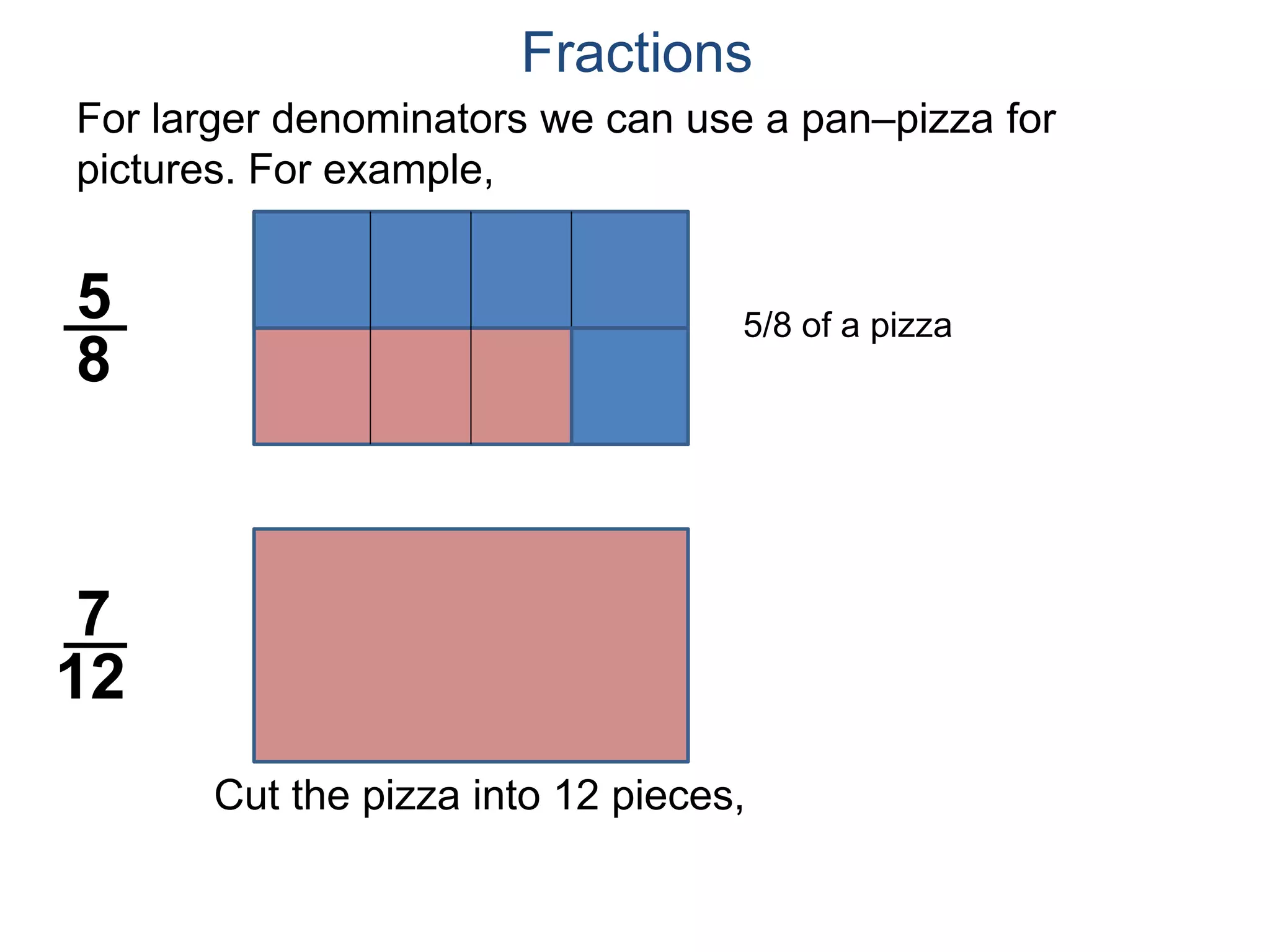
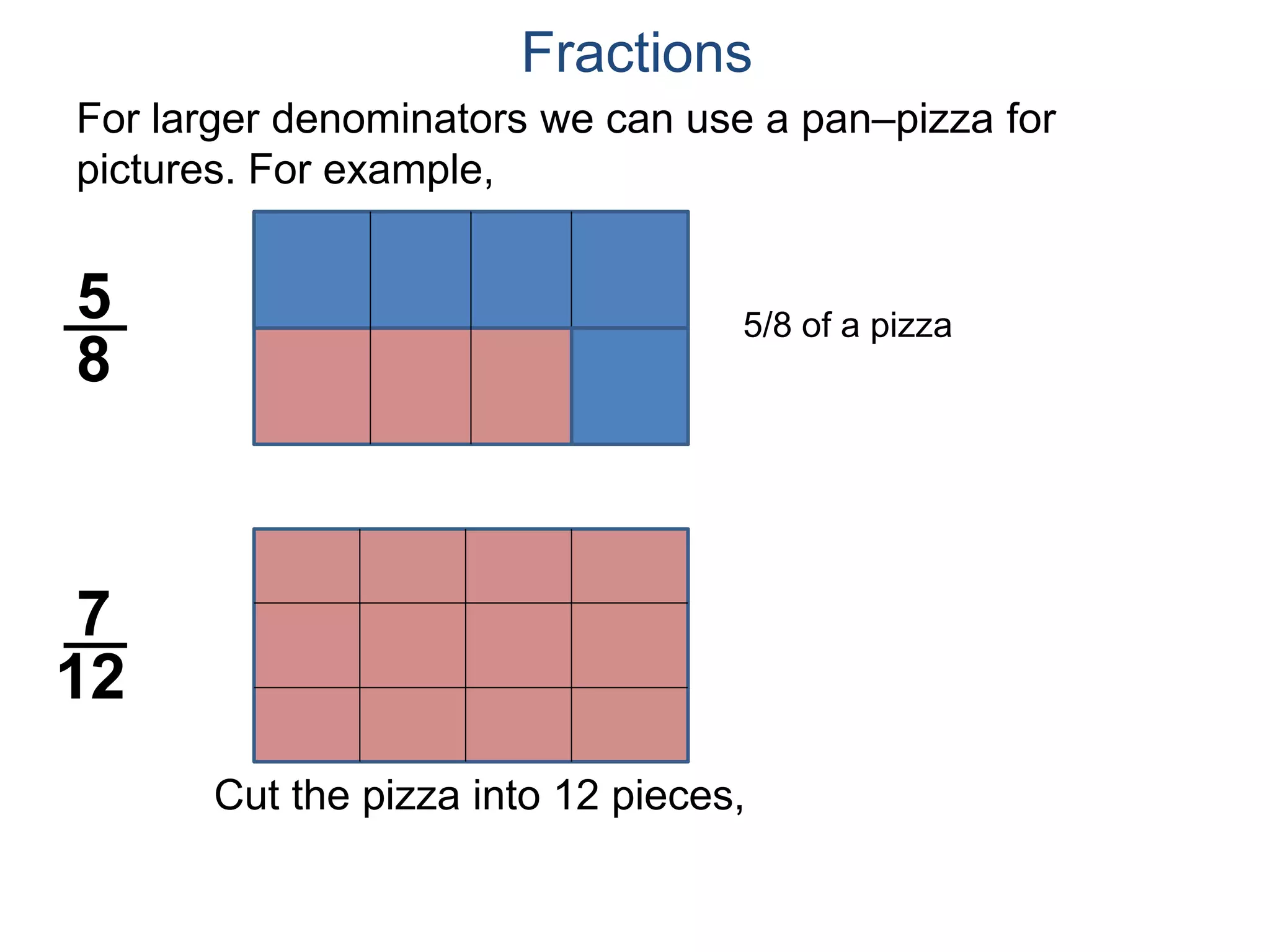
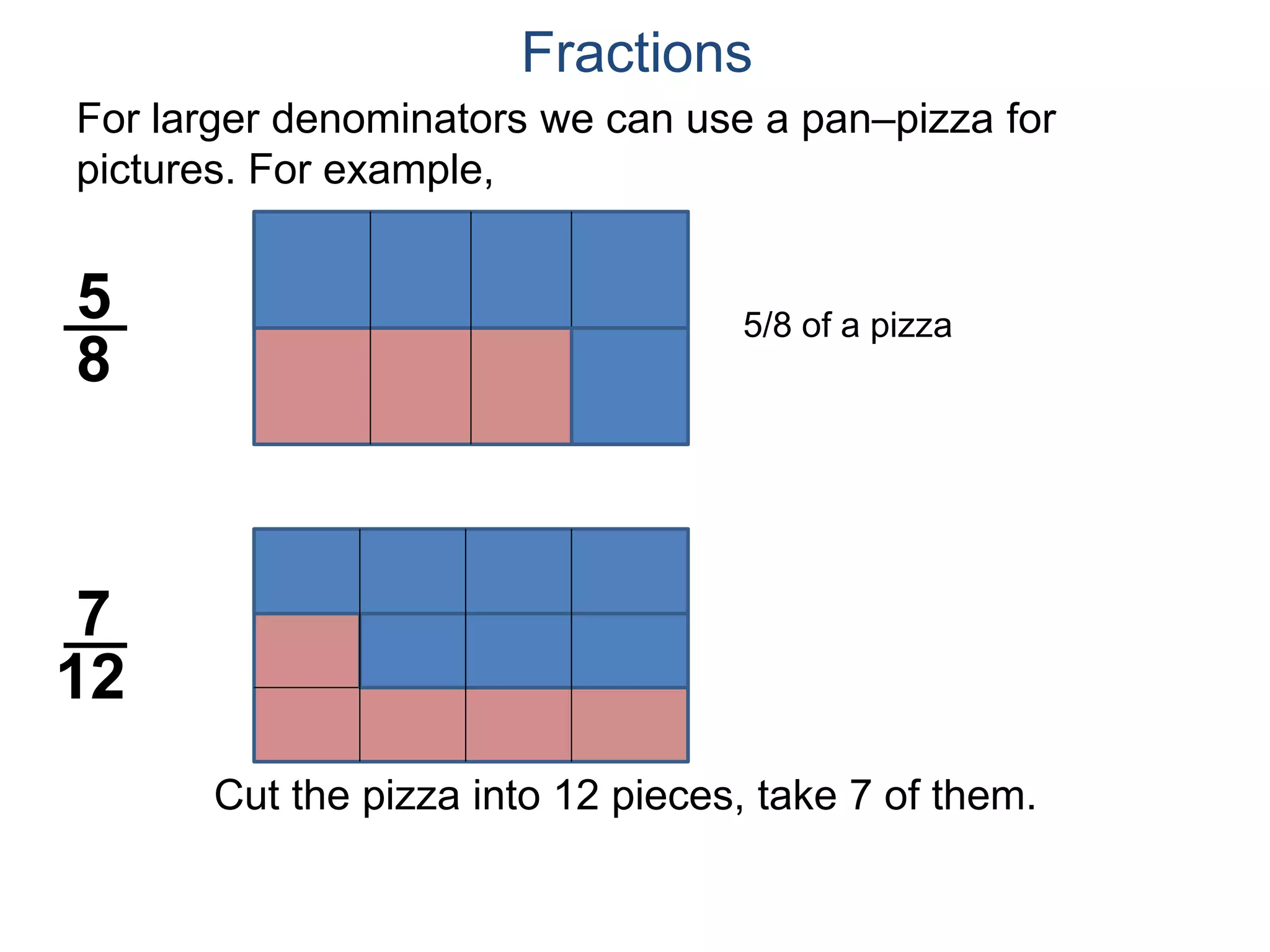
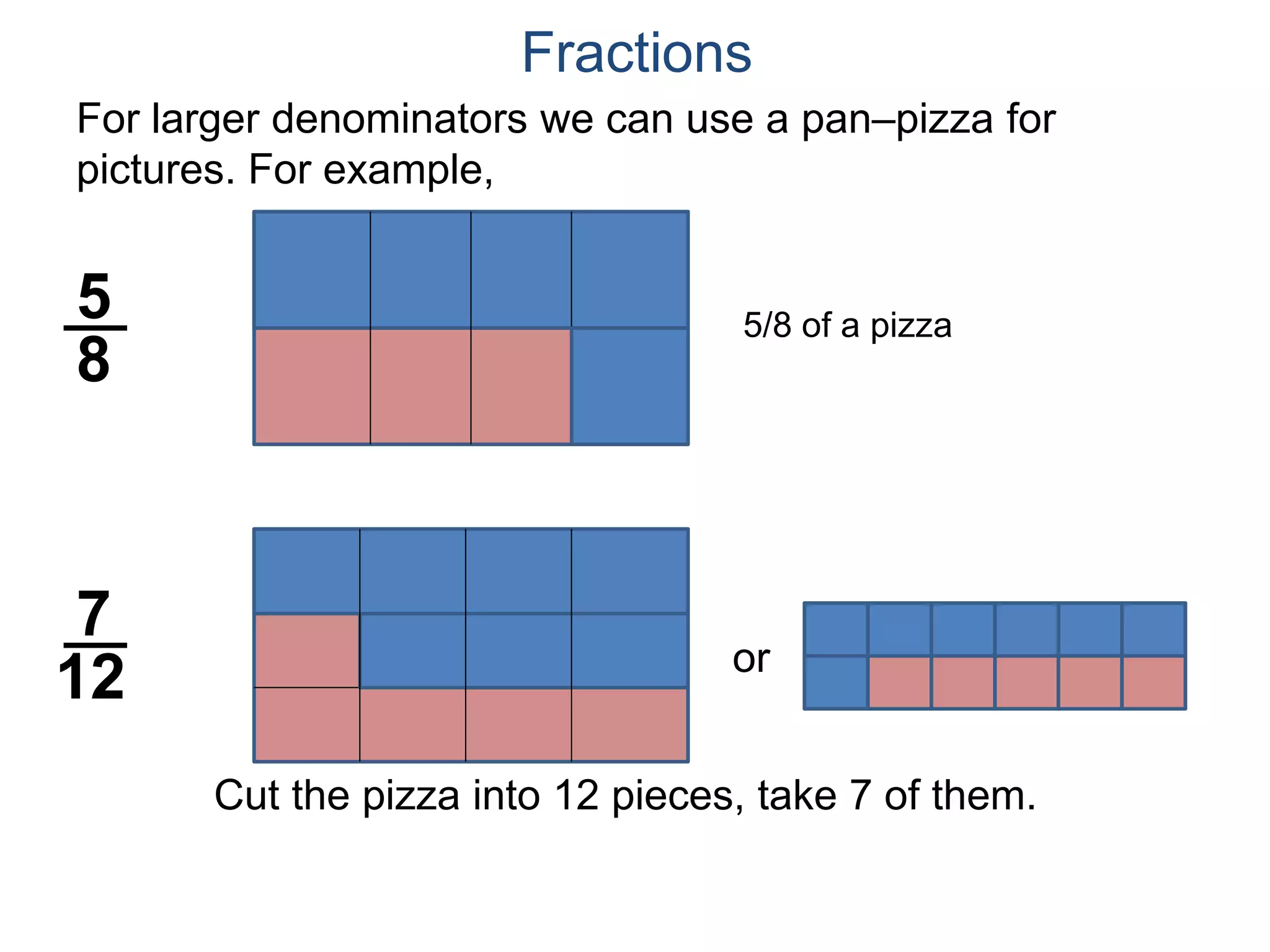
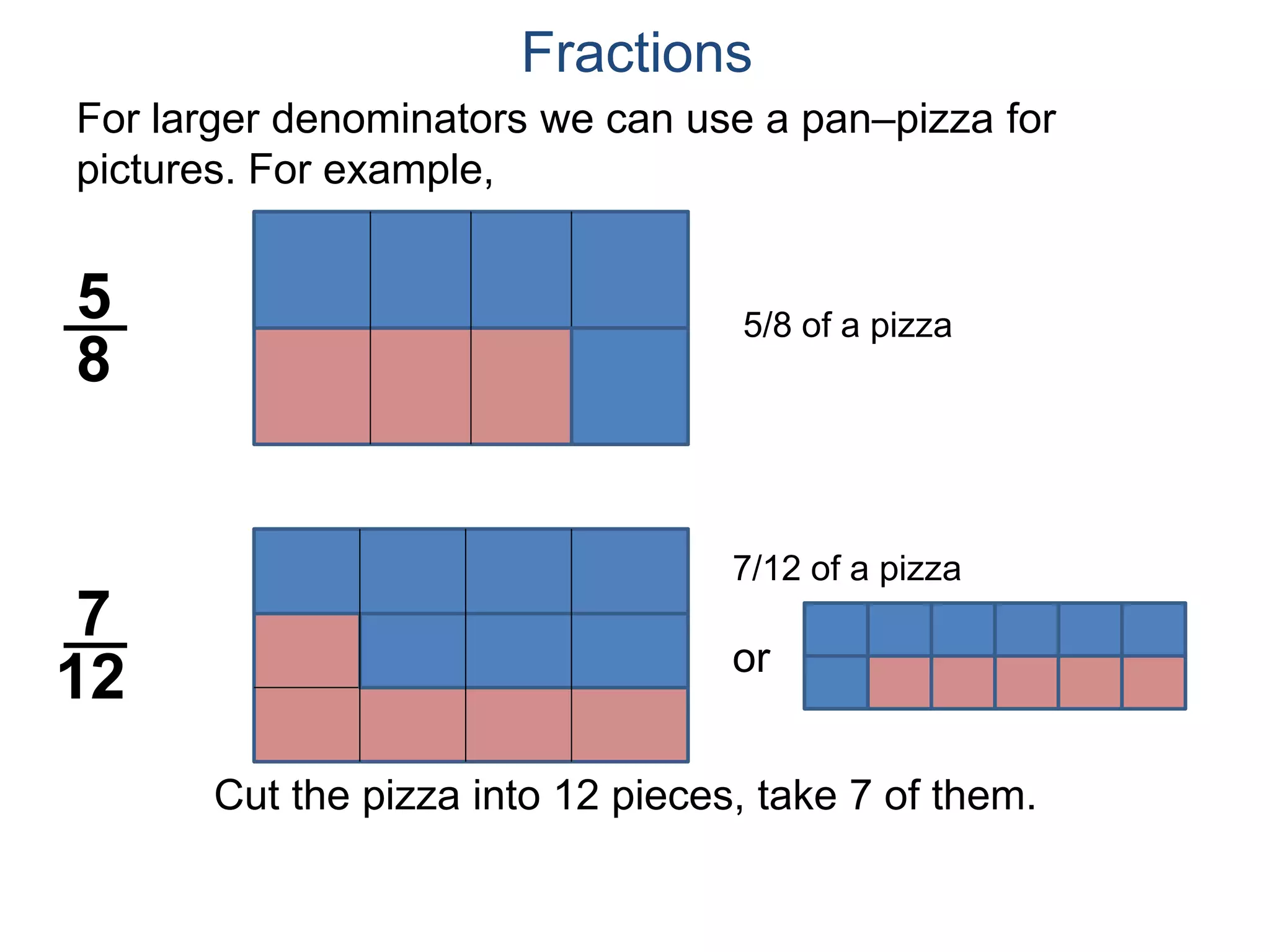
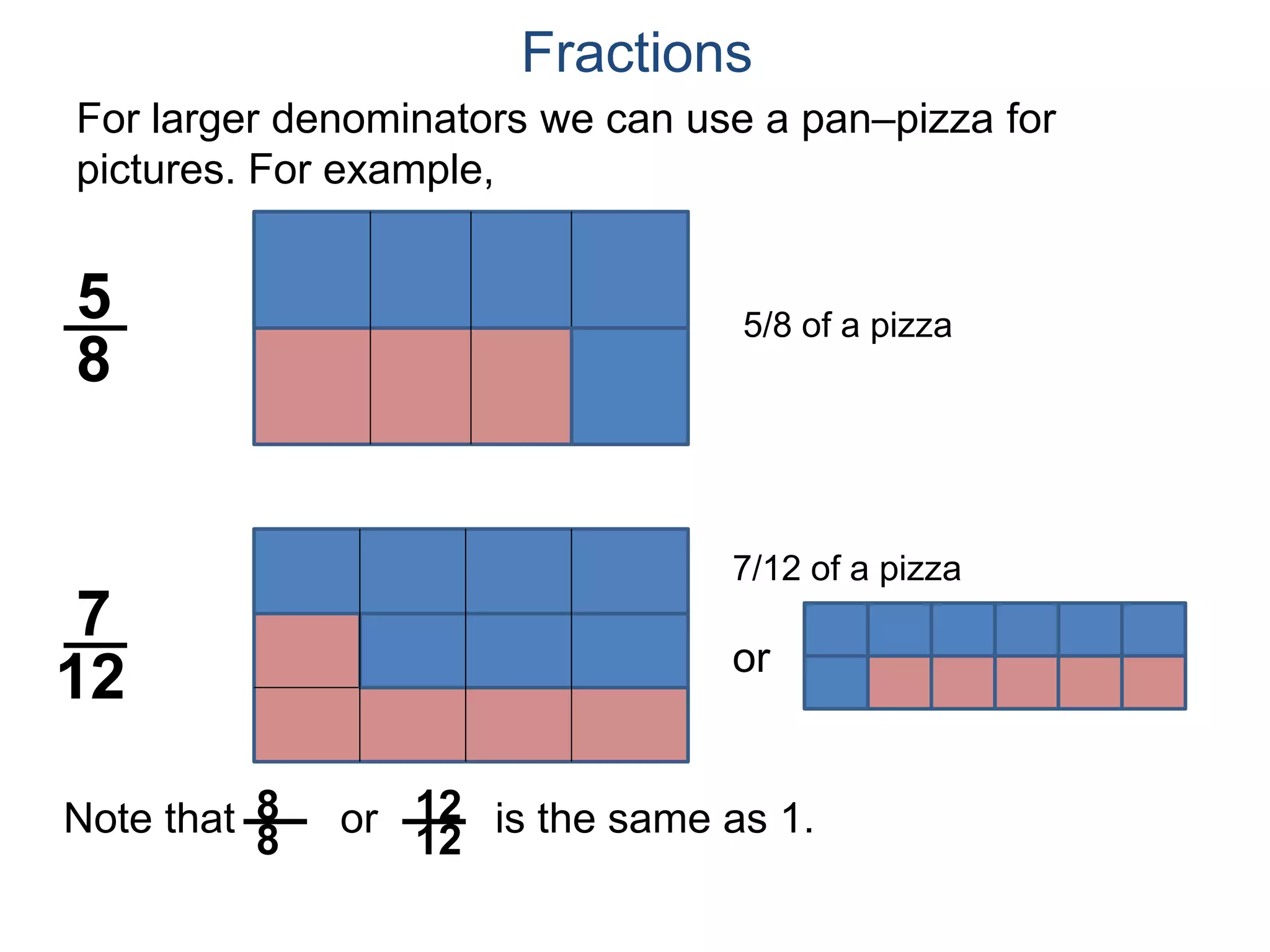
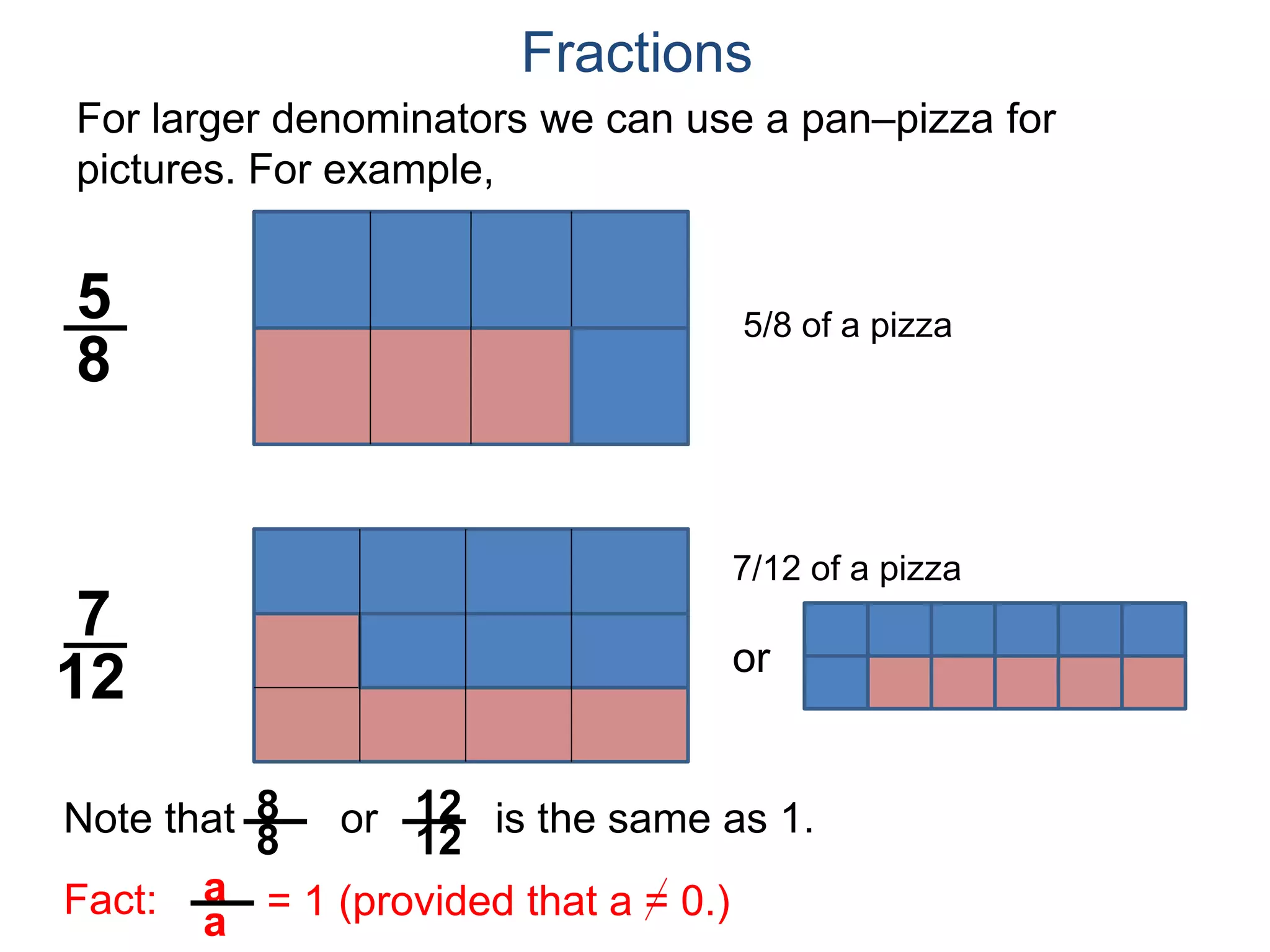
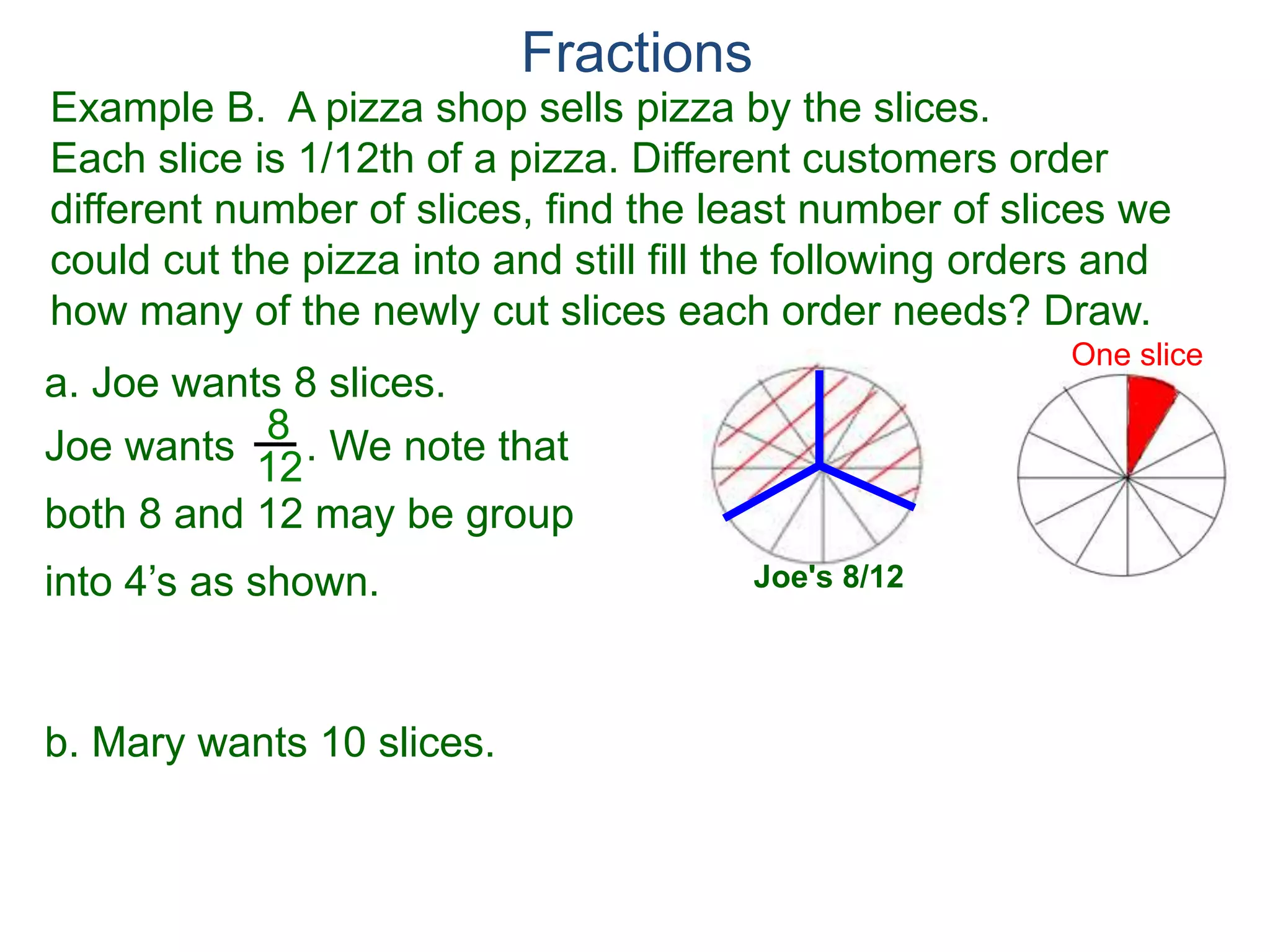
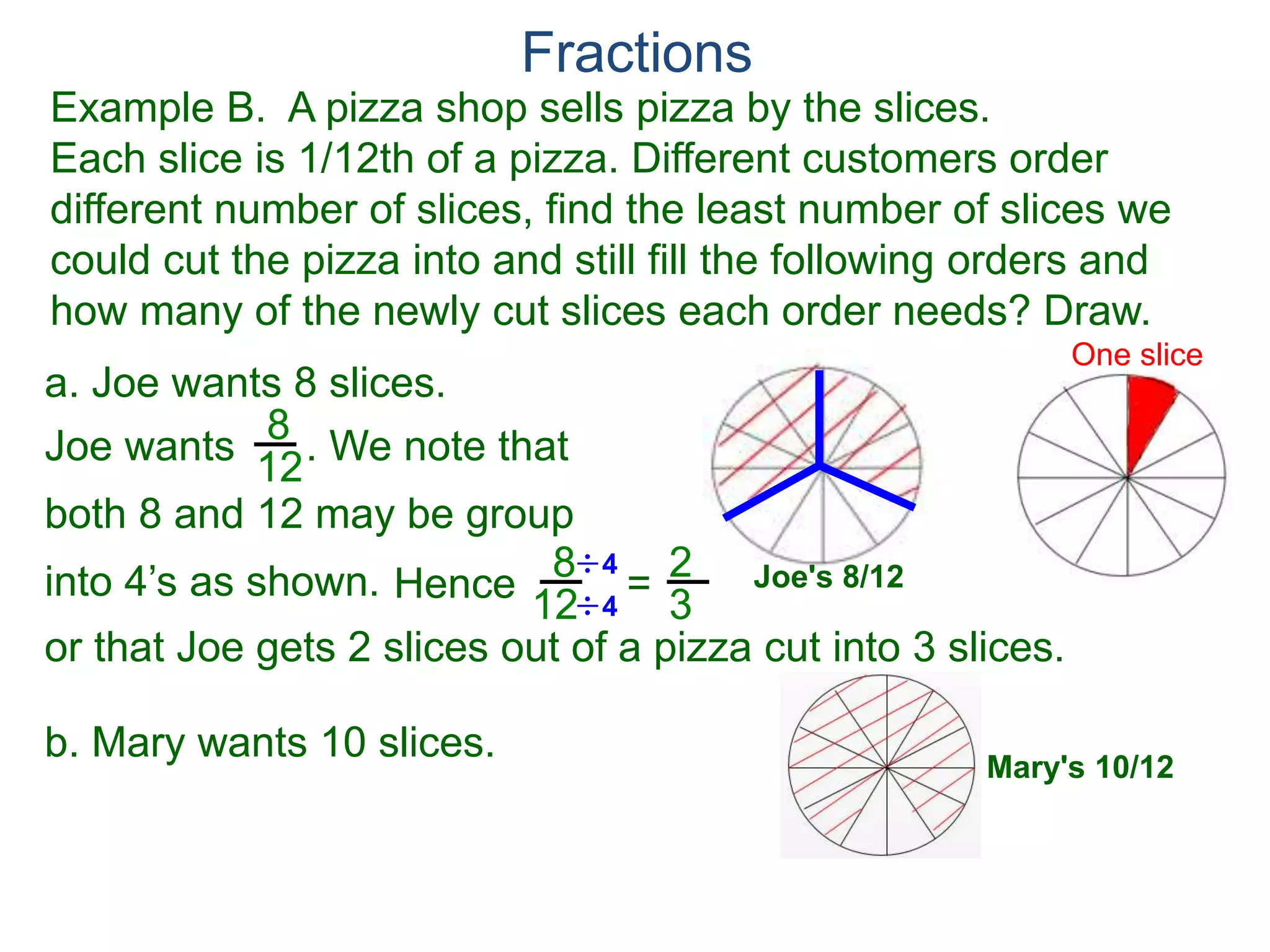
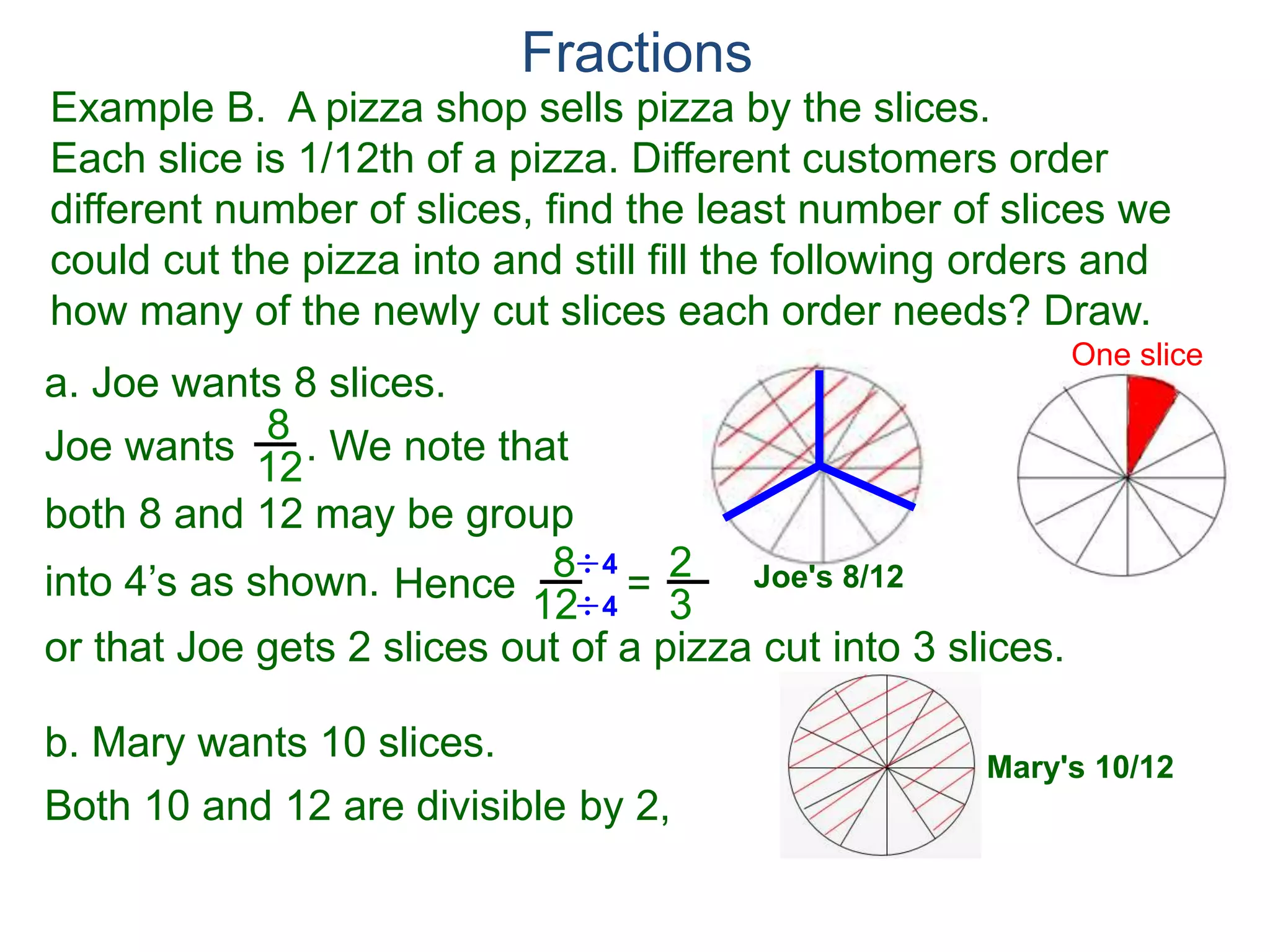
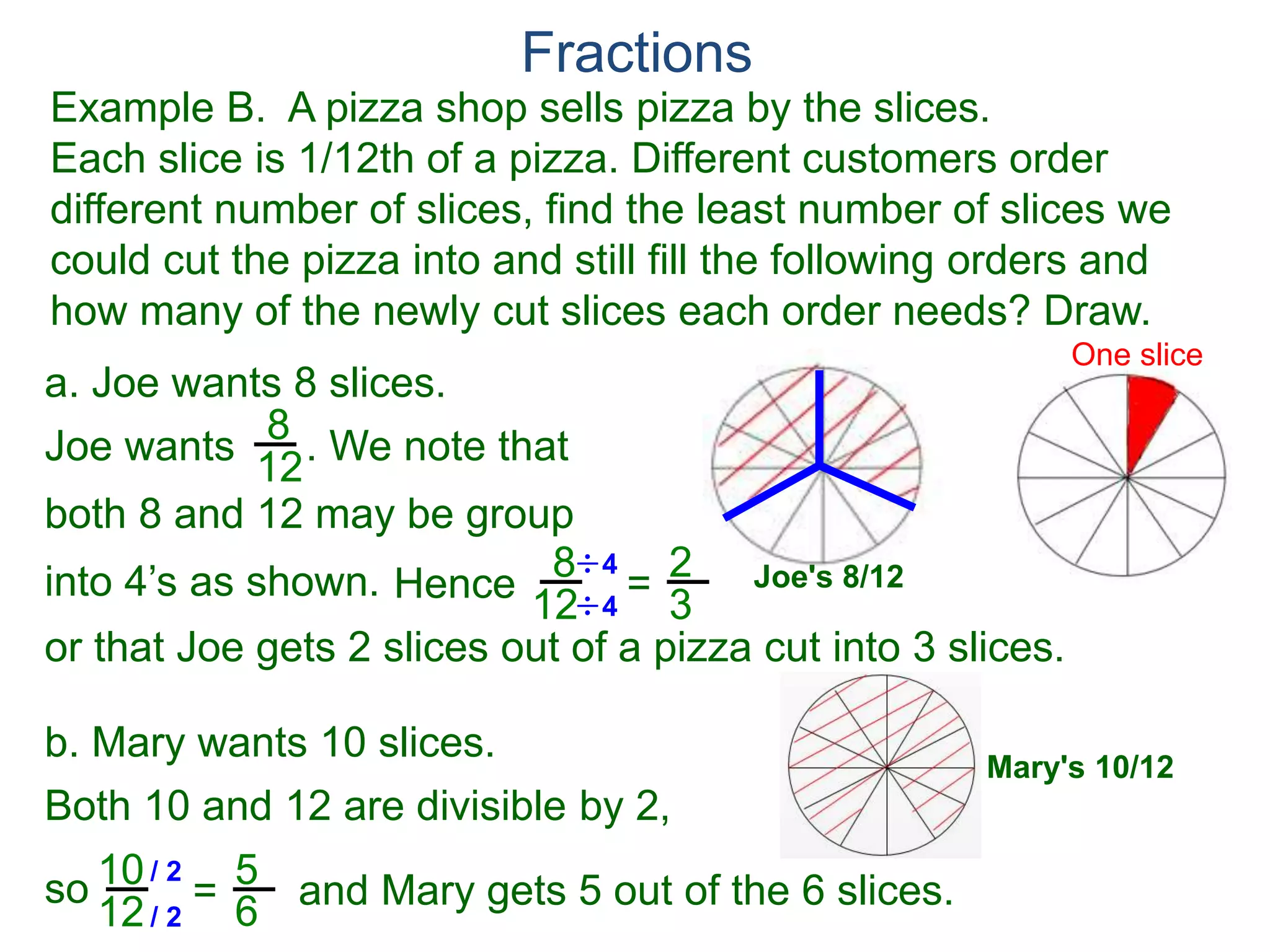
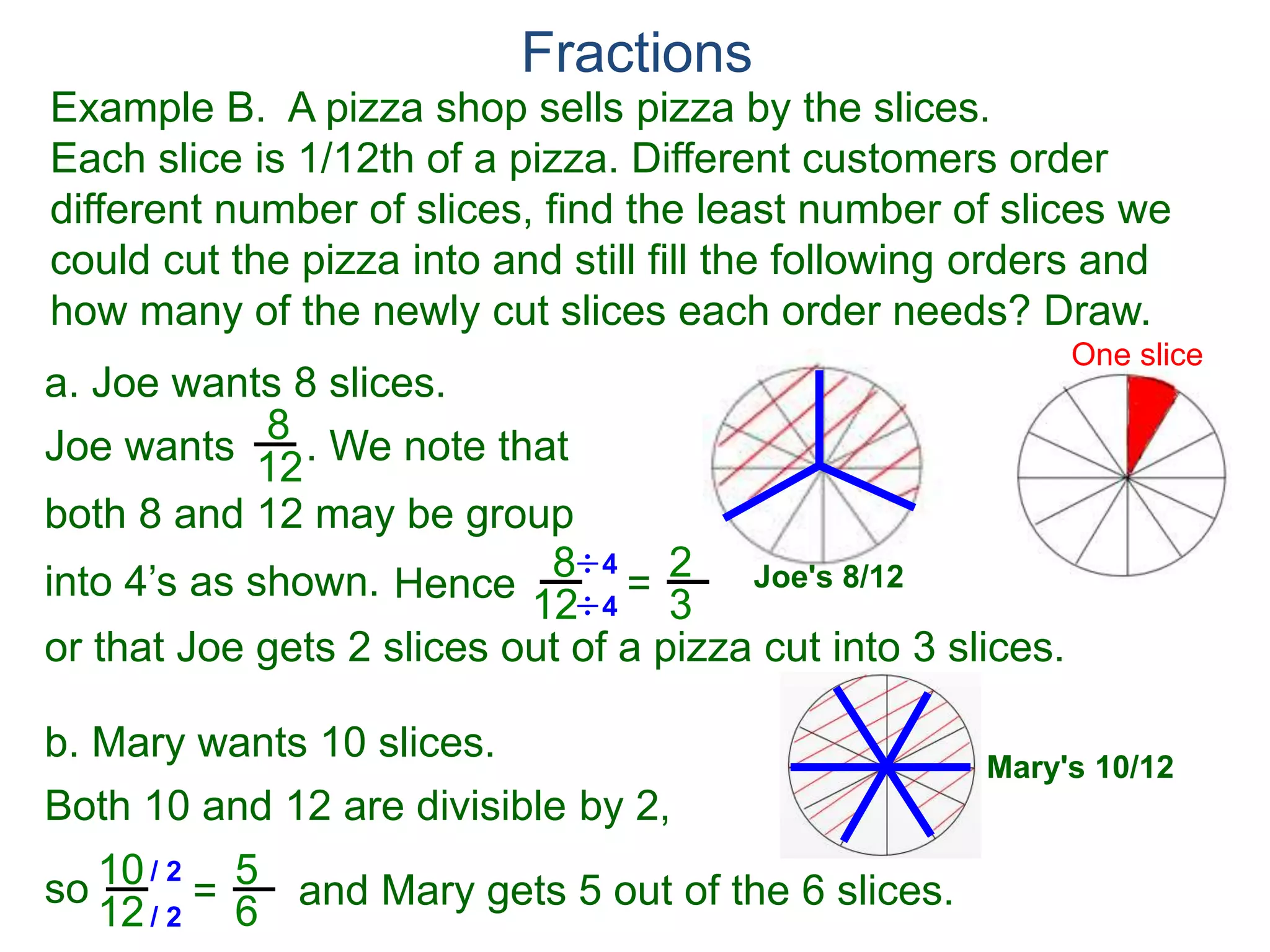
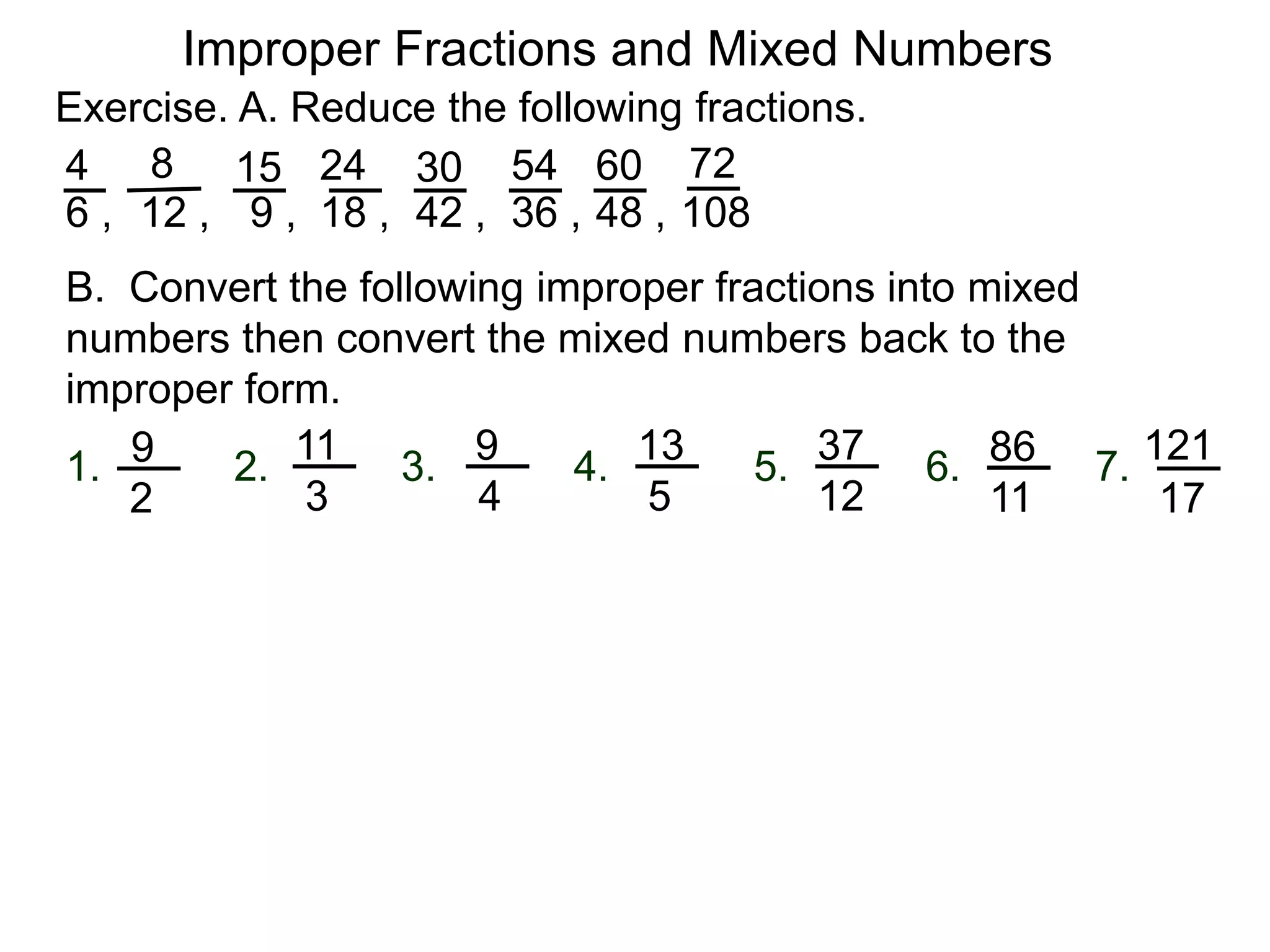The document discusses fractions and their properties. It defines fractions as numbers of the form p/q where p and q are natural numbers. Fractions represent parts of a whole, for example 3/6 represents 3 out of 6 equal slices of a pizza. The numerator is the number on top and represents the parts, while the denominator on bottom represents the total parts of the whole. Equivalent fractions like 1/2, 2/4, and 3/6 represent the same quantity. Dividing the numerator and denominator by a common factor results in an equivalent fraction. The denominator of a fraction cannot be zero, as this results in an undefined fraction.

1. Fractions
Back to 123a-Home

2. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc.
p
q
Fractions

3. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc.
p
q
Fractions
3
6

4. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
p
q
Fractions
3
6

5. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
Suppose a pizza is cut into 6 equal slices and we have 3 of
them, the fraction that represents this quantity is .
p
q
3
6
Fractions
3
6

6. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
Suppose a pizza is cut into 6 equal slices and we have 3 of
them, the fraction that represents this quantity is .
p
q
3
6
3
6
Fractions

7. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
Suppose a pizza is cut into 6 equal slices and we have 3 of
them, the fraction that represents this quantity is .
p
q
3
6
The bottom number is the
number of equal parts in the
division and it is called the
denominator.
3
6
Fractions

8. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
Suppose a pizza is cut into 6 equal slices and we have 3 of
them, the fraction that represents this quantity is .
p
q
3
6
The bottom number is the
number of equal parts in the
division and it is called the
denominator.
3
6
Fractions

9. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
Suppose a pizza is cut into 6 equal slices and we have 3 of
them, the fraction that represents this quantity is .
p
q
3
6
The bottom number is the
number of equal parts in the
division and it is called the
denominator.
The top number “3” is the
number of parts that we
have and it is called the
numerator.
3
6
Fractions

10. Fractions are numbers of the form (or p/q)
where p, q are natural numbers: 1, 2, 3,..etc. Fractions are
numbers that measure parts of whole items.
Suppose a pizza is cut into 6 equal slices and we have 3 of
them, the fraction that represents this quantity is .
p
q
3
6
The bottom number is the
number of equal parts in the
division and it is called the
denominator.
The top number “3” is the
number of parts that we
have and it is called the
numerator.
3
6
Fractions
3/6 of a pizza

11. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions

12. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
How many slices should we cut the pizza into and how do
we do this?

13. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
Cut the pizza into 8 pieces,

14. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
Cut the pizza into 8 pieces, take 5 of them.

15. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
5/8 of a pizza
Cut the pizza into 8 pieces, take 5 of them.

16. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza

17. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
Cut the pizza into 12 pieces,

18. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
Cut the pizza into 12 pieces,

19. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
Cut the pizza into 12 pieces, take 7 of them.

20. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
Cut the pizza into 12 pieces, take 7 of them.
or

21. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
7/12 of a pizza
or
Cut the pizza into 12 pieces, take 7 of them.

22. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
Note that or is the same as 1.8
8
12
12
7/12 of a pizza
or

23. For larger denominators we can use a pan–pizza for
pictures. For example,
5
8
Fractions
7
12
5/8 of a pizza
Fact: a
a
Note that or is the same as 1.8
8
12
12
= 1 (provided that a = 0.)
7/12 of a pizza
or

24. Whole numbers can be viewed as fractions with denominator 1.
Fractions

25. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = .5
1
x
1
Fractions

26. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.5
1
x
1
0
x
Fractions

27. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions

28. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:

29. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0.

30. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)

31. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)
Fractions that represents the same quantity are called
equivalent fractions.

32. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)
Fractions that represents the same quantity are called
equivalent fractions.
1
2
=
2
4

33. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)
Fractions that represents the same quantity are called
equivalent fractions.
1
2
=
2
4
=
3
6

34. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)
Fractions that represents the same quantity are called
equivalent fractions.
… are equivalent fractions.1
2
=
2
4
=
3
6
=
4
8

35. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)
Fractions that represents the same quantity are called
equivalent fractions.
… are equivalent fractions.
The fraction with the smallest denominator of all the
equivalent fractions is called the reduced fraction,
1
2
=
2
4
=
3
6
=
4
8

36. Whole numbers can be viewed as fractions with denominator 1.
Thus 5 = and x = . The fraction = 0, where x  0.
However, does not have any meaning, it is undefined.
5
1
x
1
0
x
x
0
Fractions
The Ultimate No-No of Mathematics:
The denominator (bottom) of a fraction can't
be 0. (It's undefined if the denominator is 0.)
Fractions that represents the same quantity are called
equivalent fractions.
… are equivalent fractions.
The fraction with the smallest denominator of all the
equivalent fractions is called the reduced fraction,
1
2
=
2
4
=
3
6
=
4
8
is the reduced one in the above list.
1
2

37. Fractions
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

38. Fractions
Example A. Reduce the fraction.
78
54
=b.
9
15
=a.
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

39. Fractions
Example A. Reduce the fraction.
78
54
=
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
b.
9
15
=a.
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

40. Fractions
Example A. Reduce the fraction.
78
54
=
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
b.
9
15
= 9/3
15/3
3
5=a.
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

41. Fractions
Example A. Reduce the fraction.
78
54
= 78/2
54/2
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
b.
9
15
= 9/3
15/3
3
5=a.
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

42. Fractions
Example A. Reduce the fraction.
78
54
= 78/2
54/2
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
39
27
b.
9
15
= 9/3
15/3
3
5=a.
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

43. Fractions
Example A. Reduce the fraction.
78
54
= 78/2
54/2
= 13
9
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
b.
9
15
= 9/3
15/3
3
5=a.
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

44. Fractions
Example A. Reduce the fraction.
78
54
= 78/2
54/2
= 13
9
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
b.
9
15
= 9/3
15/3
3
5=a.
(or divide by 6 directly)
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

45. Fractions
Example A. Reduce the fraction.
78
54
= 78/2
54/2
= 13
9
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
b.
9
15
= 9/3
15/3
3
5=a.
(or divide by 6 directly)
Hence a common factor of the numerator and the denominator
may be canceled as 1, so =
a * c
b * c
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

46. Fractions
Example A. Reduce the fraction.
78
54
= 78/2
54/2
= 13
9
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
b.
9
15
= 9/3
15/3
3
5=a.
(or divide by 6 directly)
Hence a common factor of the numerator and the denominator
may be canceled as 1, so
a
b
=
a * c
b * c
=
a*c
b*c*1
Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
y / c

47. Factor Cancellation Rule
For any fraction , where c ≠ 0,
that is, if the numerator and denominator are divided by the
same quantity c, the result will be an equivalent fraction.
x
y
x
y =
x / c
Fractions
y / c
Example A. Reduce the fraction.
78
54
= 78/2
54/2
= 13
9
To reduce a fraction, we keep divide the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
b.
9
15
= 9/3
15/3
3
5=a.
(or divide by 6 directly)
Hence a common factor of the numerator and the denominator
may be canceled as 1, so
a
b
=
a * c
b * c
=
a*c
b*c*1
(Often we omit writing the 1’s after the cancellation.)

48. Fractions
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.

49. Fractions
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
One slice

50. Fractions
a. Joe wants 8 slices.
b. Mary wants 10 slices.
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
One slice

51. Fractions
a. Joe wants 8 slices.
Joe wants .
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
Joe's 8/12
b. Mary wants 10 slices.
One slice

52. Fractions
a. Joe wants 8 slices.
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
Joe's 8/12
b. Mary wants 10 slices.
One slice

53. Fractions
a. Joe wants 8 slices.
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
Joe's 8/12
b. Mary wants 10 slices.
One slice

54. Fractions
a. Joe wants 8 slices.
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
or that Joe gets 2 slices out of a pizza cut into 3 slices.
b. Mary wants 10 slices.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
Joe's 8/12
One slice

55. Fractions
a. Joe wants 8 slices.
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
or that Joe gets 2 slices out of a pizza cut into 3 slices.
b. Mary wants 10 slices.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
Joe's 8/12
One slice
Mary's 10/12

56. Fractions
a. Joe wants 8 slices.
Both 10 and 12 are divisible by 2,
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
or that Joe gets 2 slices out of a pizza cut into 3 slices.
b. Mary wants 10 slices.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
Joe's 8/12
One slice
Mary's 10/12

57. Fractions
a. Joe wants 8 slices.
Both 10 and 12 are divisible by 2,
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
or that Joe gets 2 slices out of a pizza cut into 3 slices.
b. Mary wants 10 slices.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
so
Joe's 8/12
One slice
Mary's 10/12
10
12
5
6=
/ 2
/ 2

58. Fractions
a. Joe wants 8 slices.
Both 10 and 12 are divisible by 2,
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
or that Joe gets 2 slices out of a pizza cut into 3 slices.
b. Mary wants 10 slices.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
10
12
5
6=
/ 2
/ 2
so and Mary gets 5 out of the 6 slices.
Joe's 8/12
Mary's 10/12
One slice

59. Fractions
a. Joe wants 8 slices.
Both 10 and 12 are divisible by 2,
Joe wants . We note that
both 8 and 12 may be group
into 4’s as shown. Hence
8
12
2
3
=
÷4
÷4
or that Joe gets 2 slices out of a pizza cut into 3 slices.
b. Mary wants 10 slices.
8
12
Example B. A pizza shop sells pizza by the slices.
Each slice is 1/12th of a pizza. Different customers order
different number of slices, find the least number of slices we
could cut the pizza into and still fill the following orders and
how many of the newly cut slices each order needs? Draw.
so
Joe's 8/12
Mary's 10/12
One slice
and Mary gets 5 out of the 6 slices.10
12
5
6=
/ 2
/ 2

60. Common Factor Cancellation Rule
Fractions

61. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
a
b
a
b =
a / c
Fractions
b / c

62. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1,
a
b
a
b =
a / c
Fractions
b / c

63. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
=
a*c
b*c
a*c
b*c
1
Fractions
b / c

64. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c

65. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
(Often we omit writing the 1’s after the cancellation.)

66. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
(Often we omit writing the 1’s after the cancellation.)

67. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
(Often we omit writing the 1’s after the cancellation.)

68. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
(Often we omit writing the 1’s after the cancellation.)

69. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
78/2
54/2
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
(Often we omit writing the 1’s after the cancellation.)

70. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
78/2
54/2
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39
27
(Often we omit writing the 1’s after the cancellation.)

71. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
78/2
54/2
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39
27
39
27
(Often we omit writing the 1’s after the cancellation.)

72. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
78/2
54/2
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
(Often we omit writing the 1’s after the cancellation.)

73. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
78/2
54/2
= 13
9 .
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
39
27
(Often we omit writing the 1’s after the cancellation.)

74. Common Factor Cancellation Rule
Given a fraction , then
that is, if the numerator and denominator are divided by the
same factor c, the result will be an equivalent fraction.
In other words, a common factor of the numerator and the
denominator may be canceled as 1, i.e.
a
b
a
b =
a / c
a
b .
=
a*c
b*c
=
a*c
b*c
1
Fractions
b / c
Example A. Reduce the fraction .78
54
78
54
=
78/2
54/2
= 13
9 .
To reduce a fraction, we keep dividing the top and bottom by
common numbers until no more division is possible.
What's left is the reduced version.
=
39/3
27/3
or divide both by 6 in one step.
39
27
(Often we omit writing the 1’s after the cancellation.)

75. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.

76. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
A participant in a sum or a difference is called a term.

77. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).

78. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.

79. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

80. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
3
5
=
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

81. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
3
5
=
This is addition. Can’t cancel!
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

82. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
= 2 + 1
2 + 3
3
5
=
This is addition. Can’t cancel!
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

83. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
= 2 + 1
2 + 3
= 1
3
3
5
=
This is addition. Can’t cancel!
!?
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

84. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
= 2 + 1
2 + 3
= 1
3
3
5
=
This is addition. Can’t cancel!
!? 2 * 1
2 * 3
=
1
3
Yes
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

85. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
= 2 + 1
2 + 3
= 1
3
3
5
=
This is addition. Can’t cancel!
!?
Improper Fractions and Mixed Numbers
2 * 1
2 * 3
=
1
3
Yes
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

86. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
= 2 + 1
2 + 3
= 1
3
3
5
=
This is addition. Can’t cancel!
!?
A fraction whose numerator is the same or more than its
denominator (e.g. ) is said to be improper .
Improper Fractions and Mixed Numbers
3
2
2 * 1
2 * 3
=
1
3
Yes
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

87. Fractions
One common mistake in cancellation is to cancel a common
number that is part of an addition (or subtraction) in the
numerator or denominator.
2 + 1
2 + 3
= 2 + 1
2 + 3
= 1
3
3
5
=
This is addition. Can’t cancel!
!?
A fraction whose numerator is the same or more than its
denominator (e.g. ) is said to be improper .
We may put an improper fraction into mixed form by division.
Improper Fractions and Mixed Numbers
3
2
2 * 1
2 * 3
=
1
3
Yes
A participant in a sum or a difference is called a term.
The “2” in the expression “2 + 3” is a term (of the expression).
The “2” is in the expression “2 * 3” is called a factor.
Terms may not be cancelled. Only factors may be canceled.

88. 23
4
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.

89. 23
4
23 4 = 5 with remainder 3.·
·
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.

90. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 +
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4

91. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 + 5 3
4 .
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4
=

92. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 + 5 3
4 .
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4
=
We may put a mixed number into improper fraction by doing
the reverse via multiplication.

93. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 + 5 3
4 .
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4
=
We may put a mixed number into improper fraction by doing
the reverse via multiplication.
Example D. Put into improper form.5 3
4

94. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 + 5 3
4 .
5 3
4
= 4*5 + 3
4
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4
=
We may put a mixed number into improper fraction by doing
the reverse via multiplication.
Example D. Put into improper form.5 3
4

95. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 + 5 3
4 .
5 3
4
= 4*5 + 3
4
23
4
=
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4
=
We may put a mixed number into improper fraction by doing
the reverse via multiplication.
Example D. Put into improper form.5 3
4

96. 23
4
23 4 = 5 with remainder 3. Hence,·
·
23
4
= 5 + 5 3
4 .
5 3
4
= 4*5 + 3
4
23
4
=
Improper Fractions and Mixed Numbers
Example C. Put into mixed form.
3
4
=
We may put a mixed number into improper fraction by doing
the reverse via multiplication.
Example D. Put into improper form.5 3
4

97. Improper Fractions and Mixed Numbers
B. Convert the following improper fractions into mixed
numbers then convert the mixed numbers back to the
improper form.
9
2
11
3
9
4
13
5
37
12
86
11
121
17
1. 2. 3. 4. 5. 6. 7.
Exercise. A. Reduce the following fractions.
4
6 ,
8
12 ,
15
9 ,
24
18 ,
30
42 ,
54
36 ,
60
48 ,
72
108