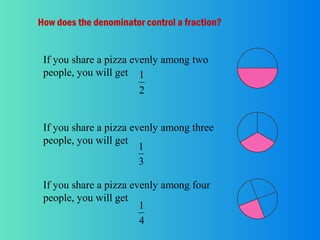
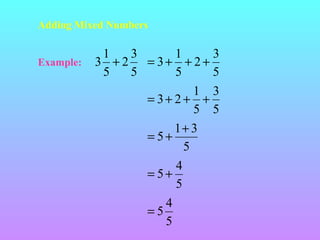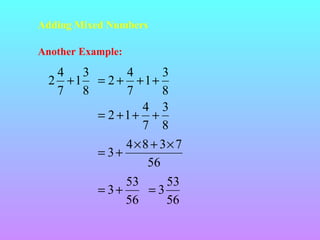The document discusses fractions including reducing fractions to lowest terms, comparing fractions, adding and subtracting fractions. It provides examples and step-by-step explanations of how to reduce fractions, convert between improper fractions and mixed numbers, find common denominators to add or subtract fractions, and perform the operations of addition and subtraction on fractions. Key points covered include how the numerator and denominator affect the size of a fraction and rules for adding and subtracting fractions including having the same denominator or finding a common denominator.

1. FRACTIONS

2. How do we know that two fractions are the same?
we cannot tell whether two fractions are the same until
we reduce them to their lowest terms.
A fraction is in its lowest terms (or is reduced) if we
cannot find a whole number (other than 1) that can divide
into both its numerator and denominator.
Examples:
6
10
is not reduced because 2 can divide into
both 6 and 10.
35
40
is not reduced because 5 divides into
both 35 and 40.

3. How do we know that two fractions are the same?
More examples:
110
260
is not reduced because 10 can divide into
both 110 and 260.
8
15
is reduced.
11
23
is reduced
To find out whether two fraction are equal, we need to
reduce them to their lowest terms.

4. How do we know that two fractions are the same?
Examples:
Are 14
21
and
30
45
equal?
14
21
reduce
14 ÷ 7 2
=
21 ÷ 7 3
30
45
reduce
30 ÷ 5 6
=
45 ÷ 5 9
reduce
6 ÷3 2
=
9 ÷3 3
Now we know that these two fractions are actually
the same!

5. How do we know that two fractions are the same?
Another example:
Are
24
40
and
30
42
equal?
24
40
reduce
24 ÷ 2 12
=
40 ÷ 2 20
30
42
reduce
30 ÷ 6 5
=
42 ÷ 6 7
reduce
12 ÷ 4 3
=
20 ÷ 4 5
This shows that these two fractions are not the same!

6. Improper Fractions and Mixed Numbers
An improper fraction is a fraction
with the numerator larger than or
equal to the denominator.
Any whole number can be
transformed into an improper
fraction.
A mixed number is a whole
number and a fraction together
5
3
4
7
4 = , 1=
1
7
3
2
7
An improper fraction can be converted to a mixed
number and vice versa.

7. Improper Fractions and Mixed Numbers
Converting improper fractions into
mixed numbers:
- divide the numerator by the denominator
- the quotient is the leading number,
- the remainder as the new numerator.
More examples:
Converting mixed numbers
into improper fractions.
5
2
=1
3
3
7
3
=1 ,
4
4
11
1
=2
5
5
3 2 × 7 + 3 17
2 =
=
7
7
7

8. How does the denominator control a fraction?
If you share a pizza evenly among two
people, you will get 1
2
If you share a pizza evenly among three
people, you will get
1
3
If you share a pizza evenly among four
people, you will get
1
4

9. How does the denominator control a fraction?
If you share a pizza evenly among eight
people, you will get only 1
8
It’s not hard to see that the slice you get
becomes smaller and smaller.
Conclusion:
The larger the denominator the smaller the pieces,
and if the numerator is kept fixed, the larger the
denominator the smaller the fraction,

10. Examples:
2
2
or ?
Which one is larger,
7
5
2
Ans :
5
8
8
or
?
Which one is larger,
23
25
8
Ans :
23
41
41
or
?
Which one is larger,
135
267
41
Ans :
135

11. How does the numerator affect a fraction?
Here is 1/16 ,
here is 3/16 ,
here is 5/16 ,
Do you see a trend?
Yes, when the numerator gets larger
we have more pieces.
And if the denominator is kept fixed,
the larger numerator makes a bigger
fraction.

12. Examples:
7
5
or
?
Which one is larger,
12
12
7
Ans :
12
8
13
or
?
Which one is larger,
20
20
13
Ans :
20
45
63
or
?
Which one is larger,
100
100
63
Ans :
100

13. Comparing fractions with different numerators and
different denominators.
In this case, it would be pretty difficult to tell just from
the numbers which fraction is bigger, for example
3
8
This one has less pieces
but each piece is larger
than those on the right.
5
12
This one has more pieces
but each piece is smaller
than those on the left.

14. 3
8
5
12
The FIRST WAY to answer this question is to change the
appearance of the fractions so that the denominators are the
same.
In that case, the pieces are all of the same size, hence the
larger numerator makes a bigger fraction.
The SECOND WAY to find a common denominator is to
multiply the two denominators together:
3 3 × 12 36
=
=
8 8 × 12 96
and
5
5 × 8 40
=
=
12 12 × 8 96
Now it is easy to tell that 5/12 is actually a bit bigger than 3/8.

15. A more efficient way to compare fractions
Which one is larger,
7
5
or
?
11
8
From the previous example, we see that we don’t
really have to know what the common denominator
turns out to be, all we care are the numerators.
Therefore we shall only change the numerators by
cross multiplying.
7 × 8 = 56
Since 56 > 55, we see that
7
11
5
8
11 × 5 = 55
7 5
>
11 8
This method is called cross-multiplication, and make sure that you
remember to make the arrows go upward.

16. Addition of Fractions
- addition means combining objects in two or
more sets
- the objects must be of the same type, i.e. we
combine bundles with bundles and sticks with
sticks.
- in fractions, we can only combine pieces of the
same size. In other words, the denominators
must be the same.

17. Addition of Fractions with equal denominators
1 3
8 8
Example: +
+
Click to see animation
= ?

18. Addition of Fractions with equal denominators
1 3
8 8
Example: +
+
=

19. Addition of Fractions with equal denominators
1 3
8 8
Example: +
+
The answer is
=
(1 + 3)
which can be simplified to 1
2
8

20. Addition of Fractions with equal denominators
More examples
2 1
3
+ =
5 5
5
6 7
13
3
+ =
= 1
10 10
10
10
6 8
14
+ =
15 15
15

21. Addition of Fractions with
different denominators
In this case, we need to first convert them into equivalent
fraction with the same denominator.
Example:
1 2
+
3 5
An easy choice for a common denominator is 3×5 = 15
1 1× 5 5
=
=
3 3 × 5 15
Therefore,
2 2×3 6
=
=
5 5 × 3 15
1 2 5 6 11
+ = +
=
3 5 15 15 15

22. Addition of Fractions with
different denominators
You have to multiply the two denominators together, antd
that number would be your COMMON DENOMINATOR
for both fractions.
REMEMBER: If you amplified the denominator you must
also multiply the denominator by the same number.

23. More Exercises:
3 1
3× 2 1
6 1
6 +1 7
+ =
+ = + =
=
4 8
4× 2 8
8 8
8
8
3 2
3× 7 2 × 5
21 10
+ =
+
+
=
5 7
5× 7 7 ×5
35 35
21 + 10 31
=
=
35
35
5 4
5×9 4× 6
45 24
+ =
+
+
=
6 9
6×9 9×6
54 54
45 + 24 69
15
=
=1
=
54
54
54

24. Adding Mixed Numbers
Example:
1
3
1
3
3 + 2 = 3+ + 2+
5
5
5
5
1 3
= 3+ 2+ +
5 5
1+ 3
= 5+
5
4
= 5+
5
4
=5
5

25. Adding Mixed Numbers
Another Example:
4 3
4
3
2 +1 = 2 + +1+
7 8
7
8
4 3
= 2 +1+ +
7 8
4 × 8 + 3× 7
= 3+
56
53
53
= 3+
=3
56
56

26. Subtraction of Fractions
- subtraction means taking objects away.
- the objects must be of the same type, i.e. we
can only take away apples from a group of
apples.
- in fractions, we can only take away pieces of
the same size. In other words, the denominators
must be the same.

27. Subtraction of Fractions with equal denominators
Example: 11 − 3
12 12
This means to take away
11
12
(Click to see animation)
3 from 11
12
12
take
a wa
y

28. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
11
12
3 from 11
12
12

29. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

30. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

31. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

32. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

33. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

34. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

35. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

36. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

37. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

38. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

39. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

40. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

41. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

42. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

43. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

44. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

45. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

46. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

47. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12

48. Subtraction of Fractions with equal denominators
Example:
11 3
−
12 12
This means to take away
3 from 11
12
12
Now you can see that there are only 8 pieces left,
therefore
11 3 11 − 3
− =
12 12
12

49. Subtraction of Fractions
More examples:
15 7
15 − 7
8
1
− =
=
=
16 16
16
16 2
6 4
6×9 4×7
54 28 54 − 28
26
− =
−
=
−
=
=
7 9
7×9 9×7
63 63
63
63
7 11
7 × 23 11× 10
7 × 23 − 11× 10
161− 110
−
=
−
=
=
10 23 10 × 23 23 ×10
10 × 23
230
51
=
230
Did you get all the answers right?

50. Subtraction of mixed numbers
This is more difficult than before, so please take notes.
1
1
Example: 3 − 1
4
2
Since 1/4 is not enough to be subtracted by 1/2, we better convert
all mixed numbers into improper fractions first.
1
1
3 × 4 + 1 1× 2 + 1
3 −1 =
−
4
2
4
2
13
3
=
−
4
2
13
6
=
−
4
4
7
3
=
=1
4
4