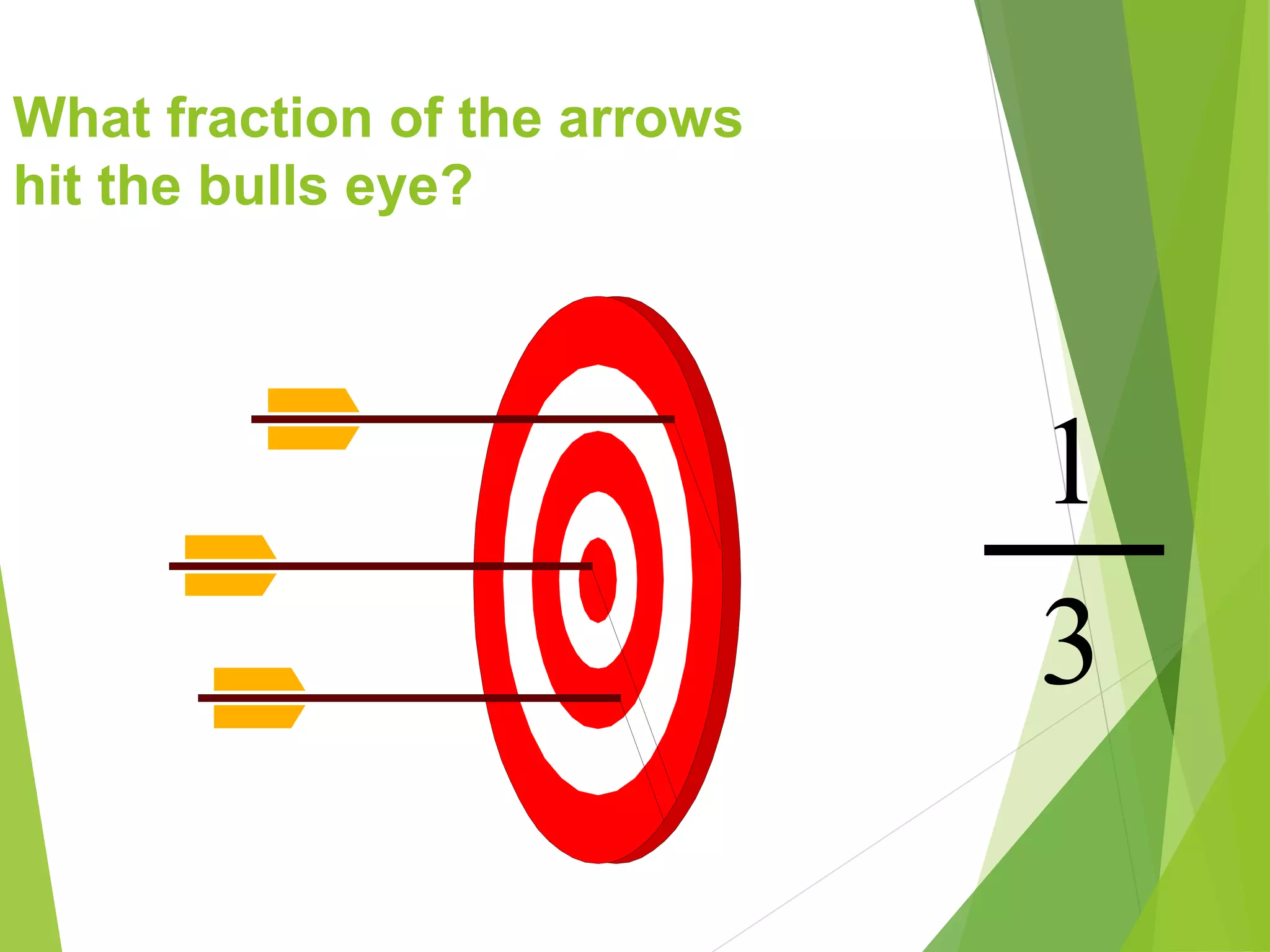
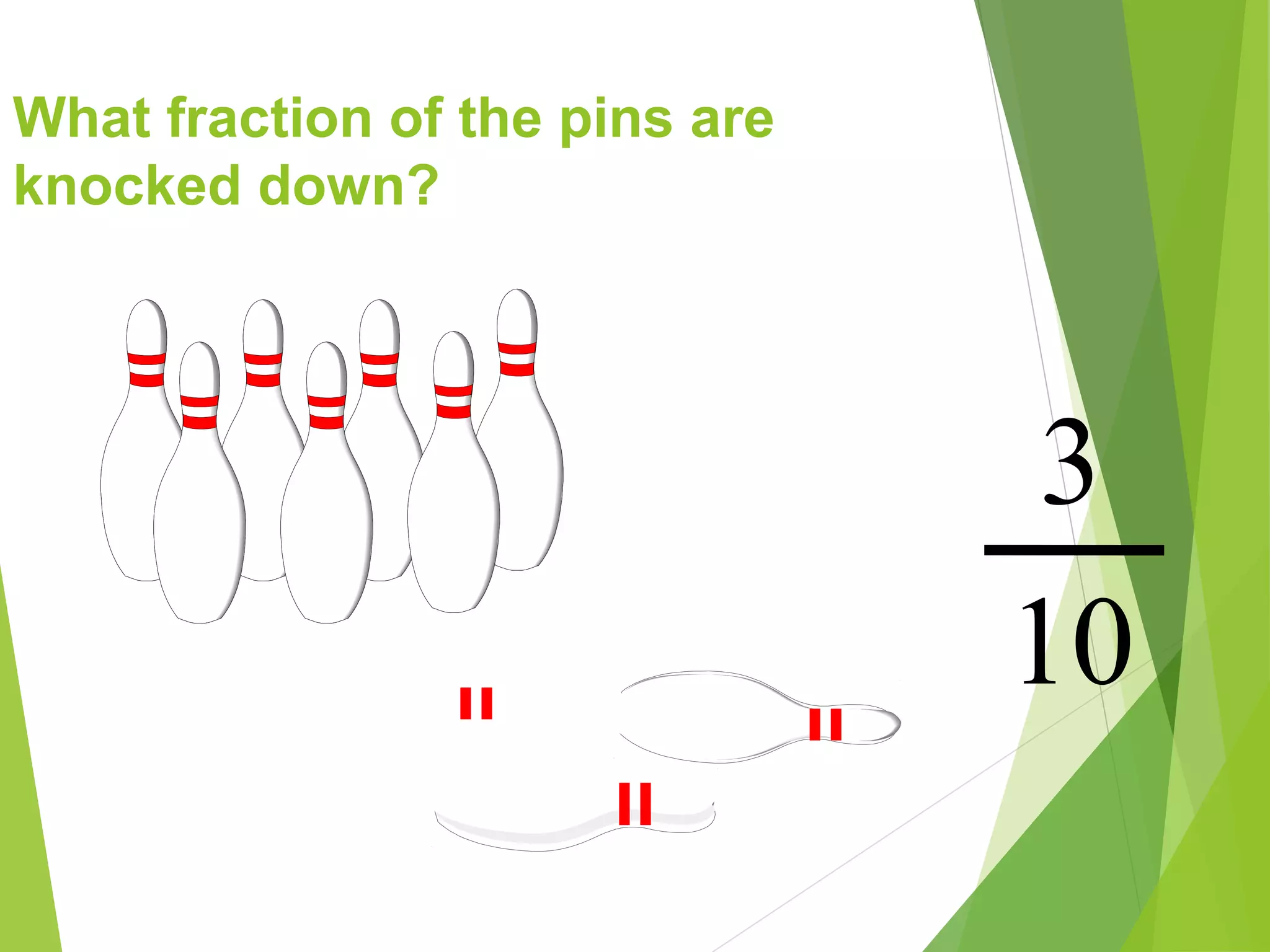
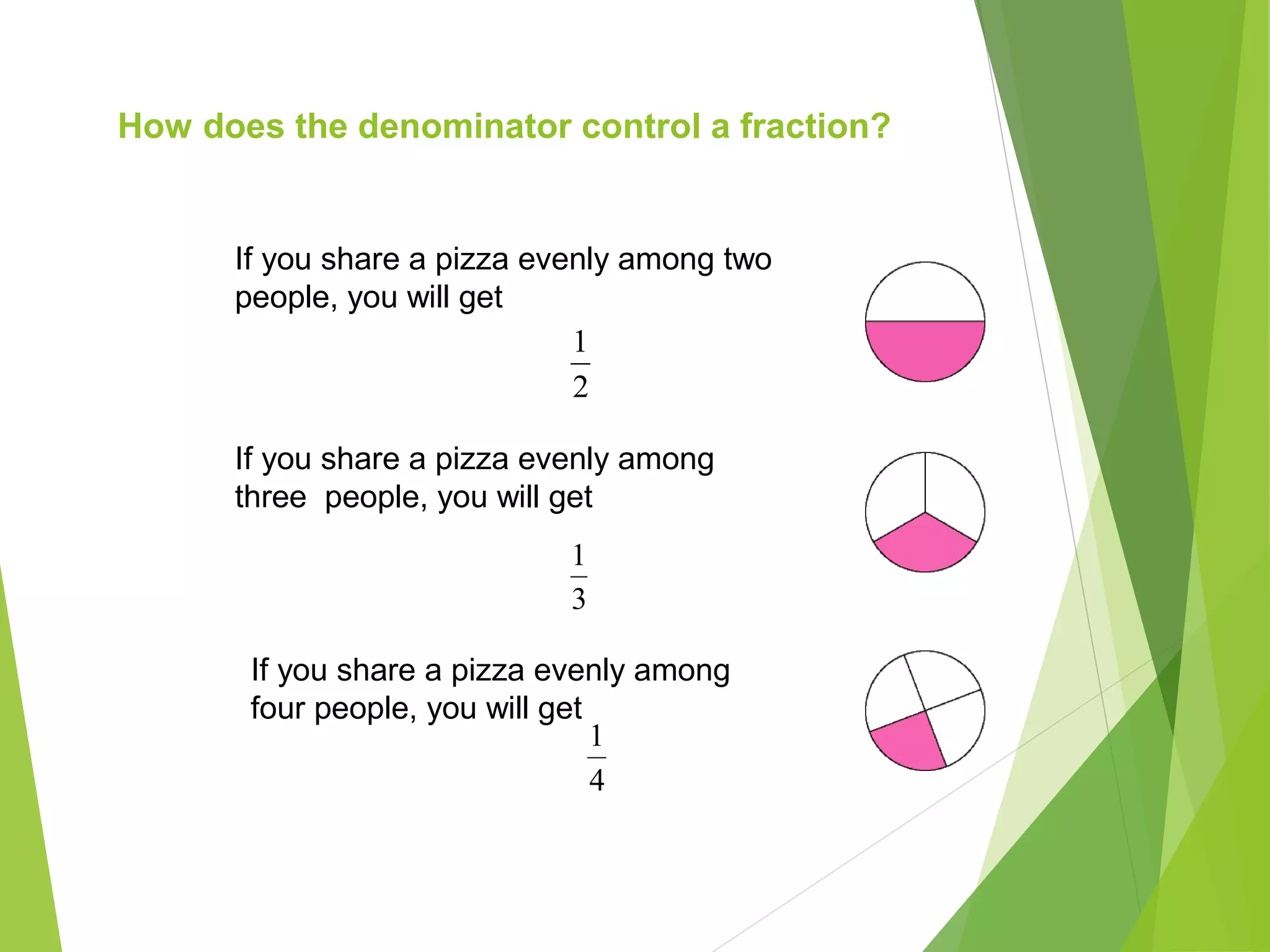
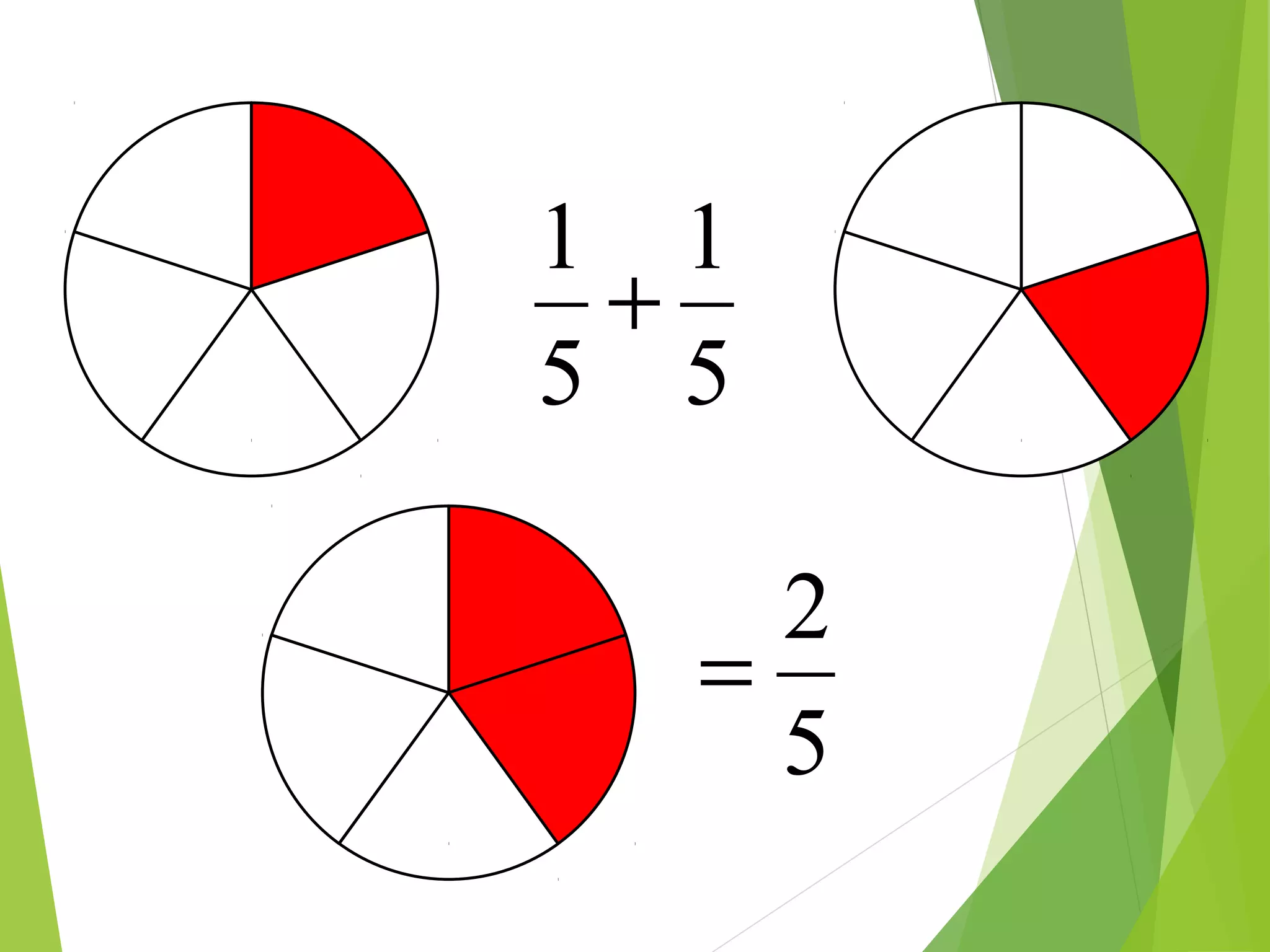
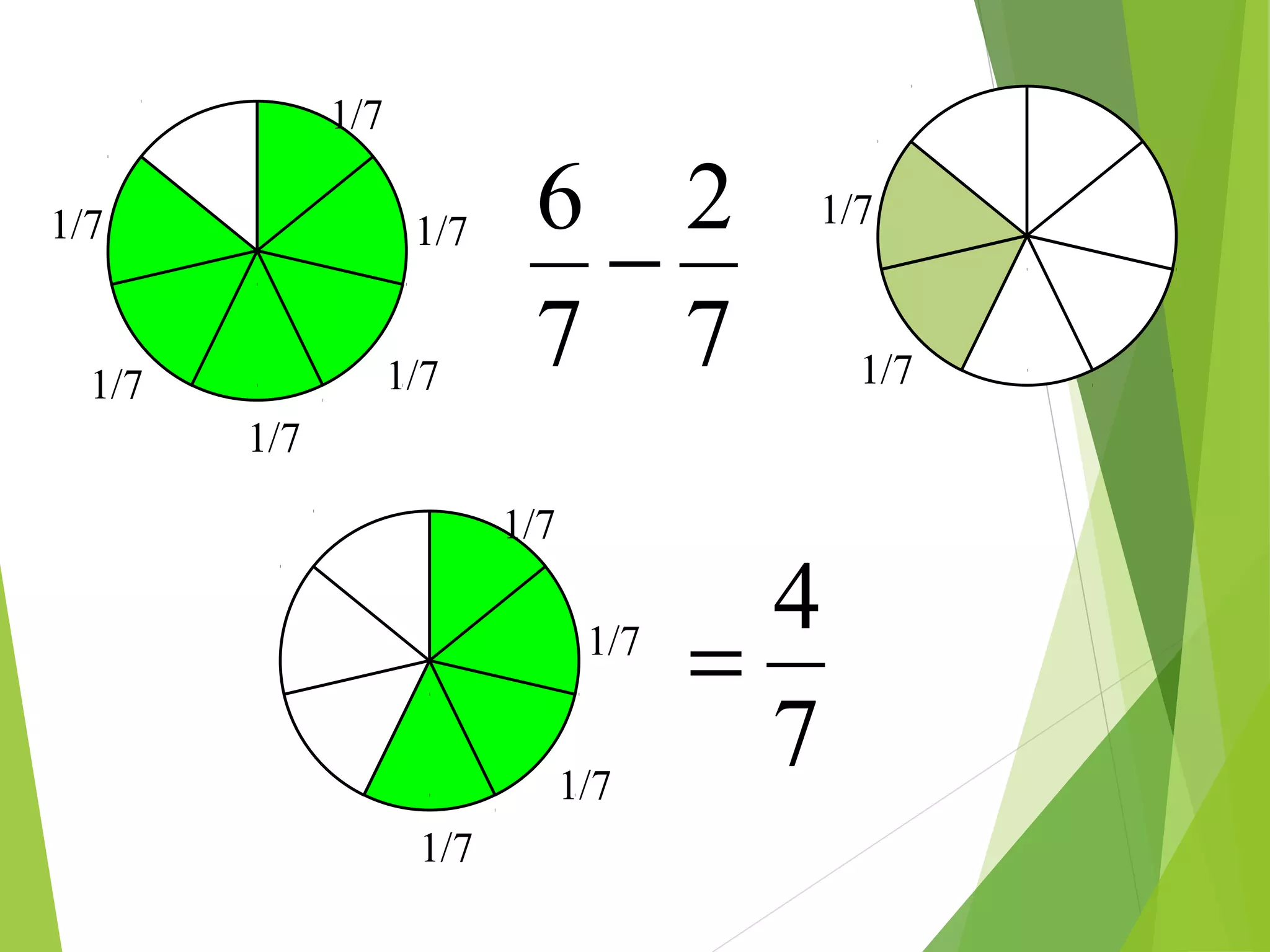
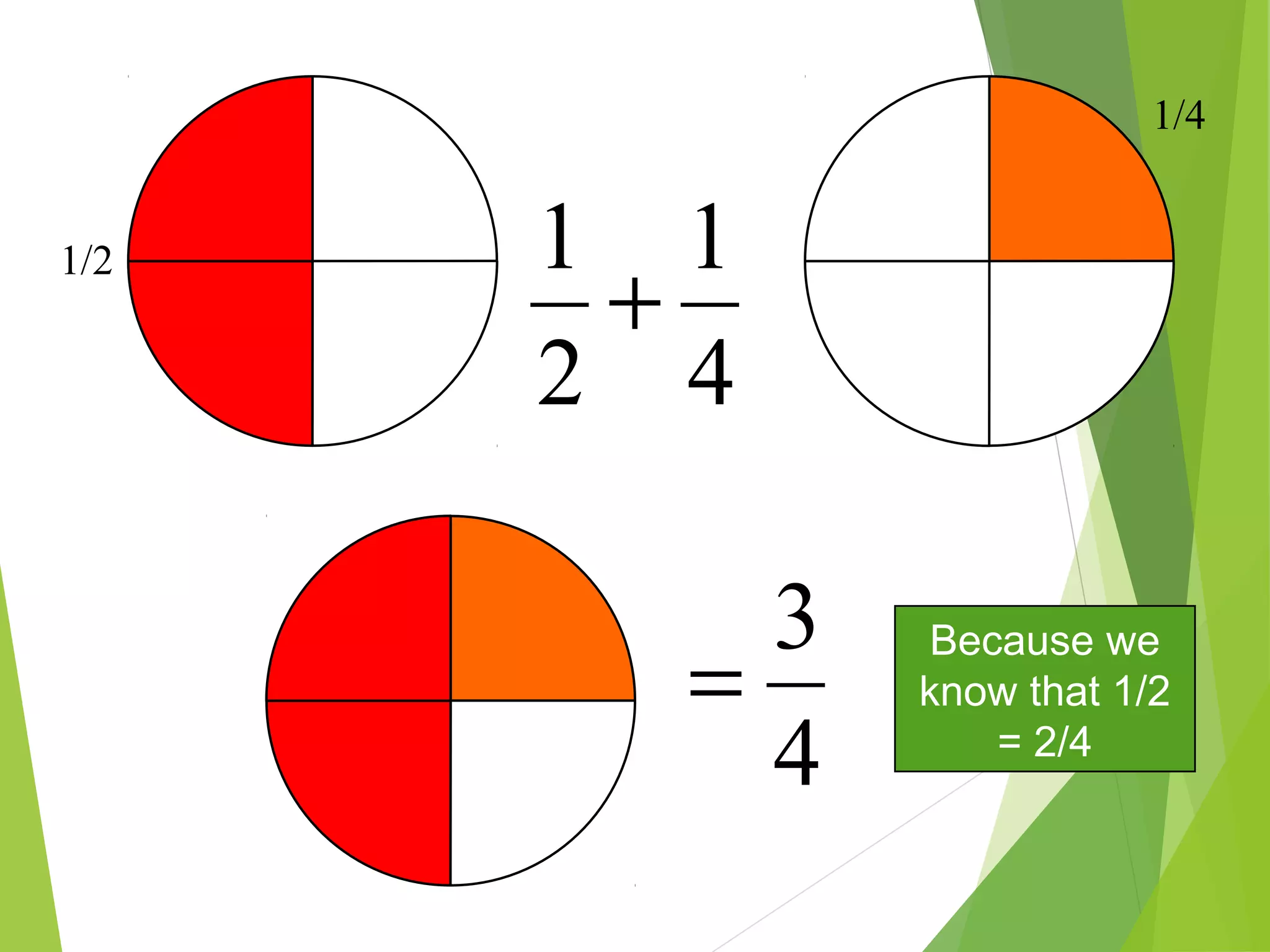
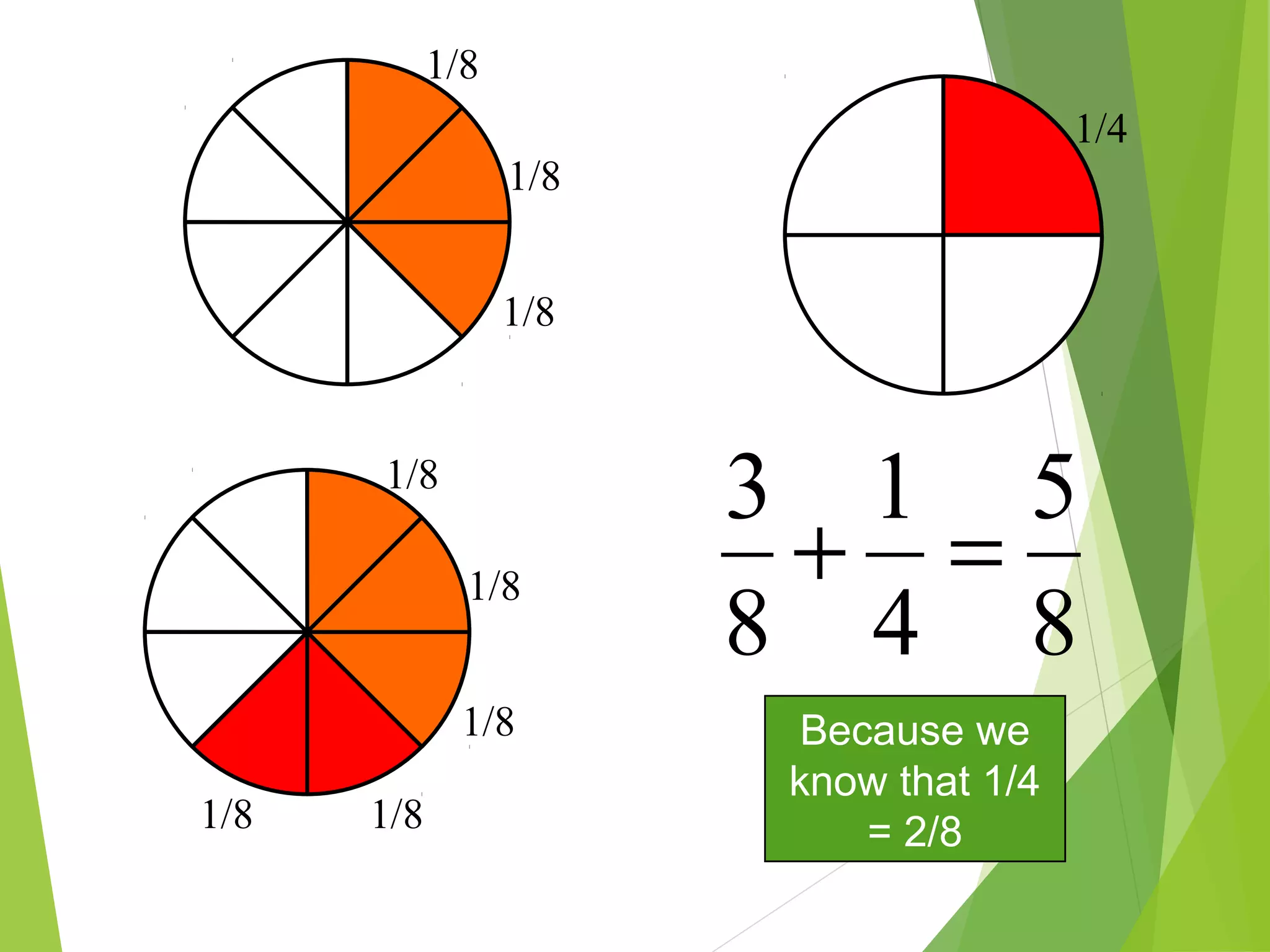
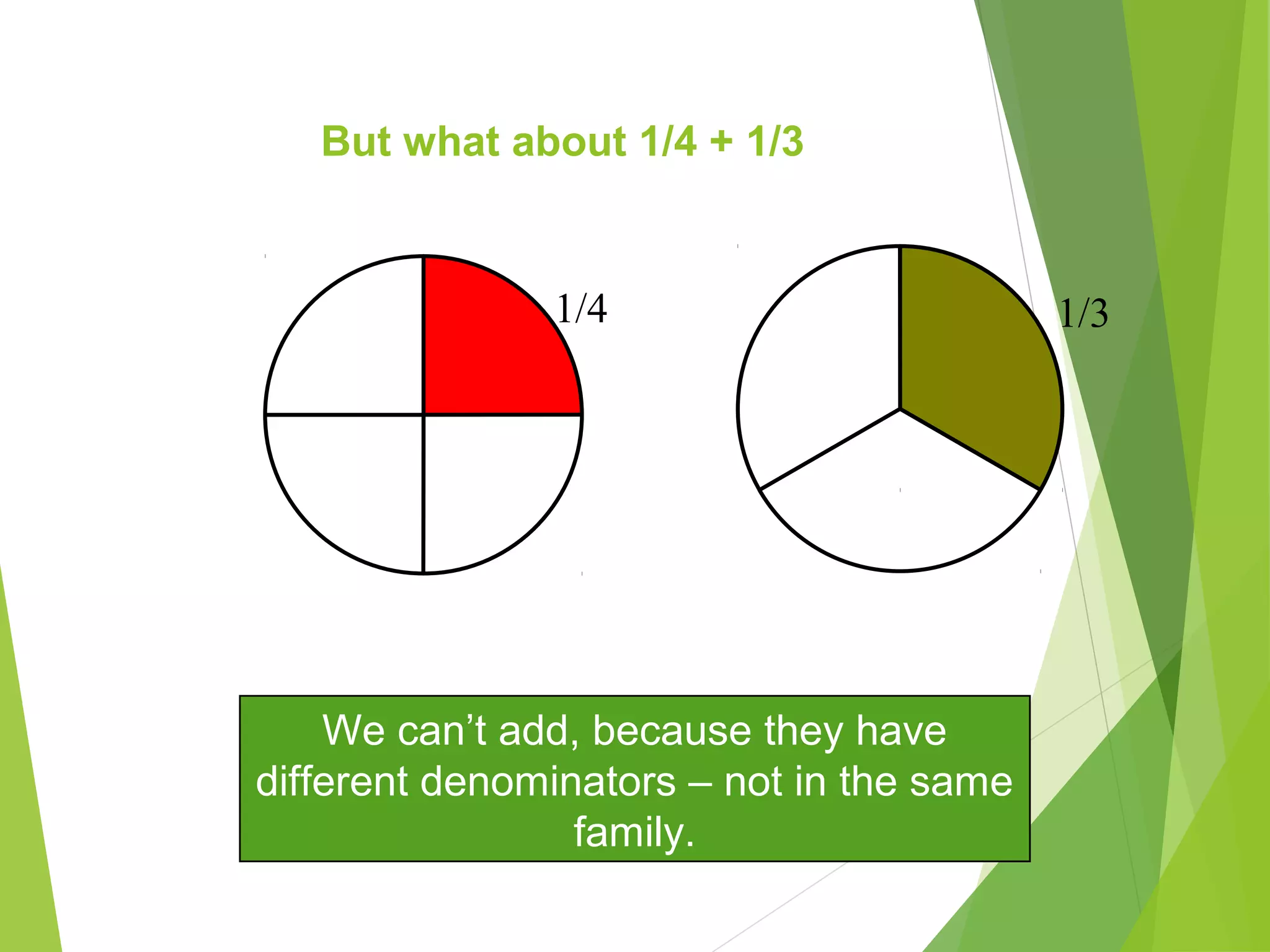
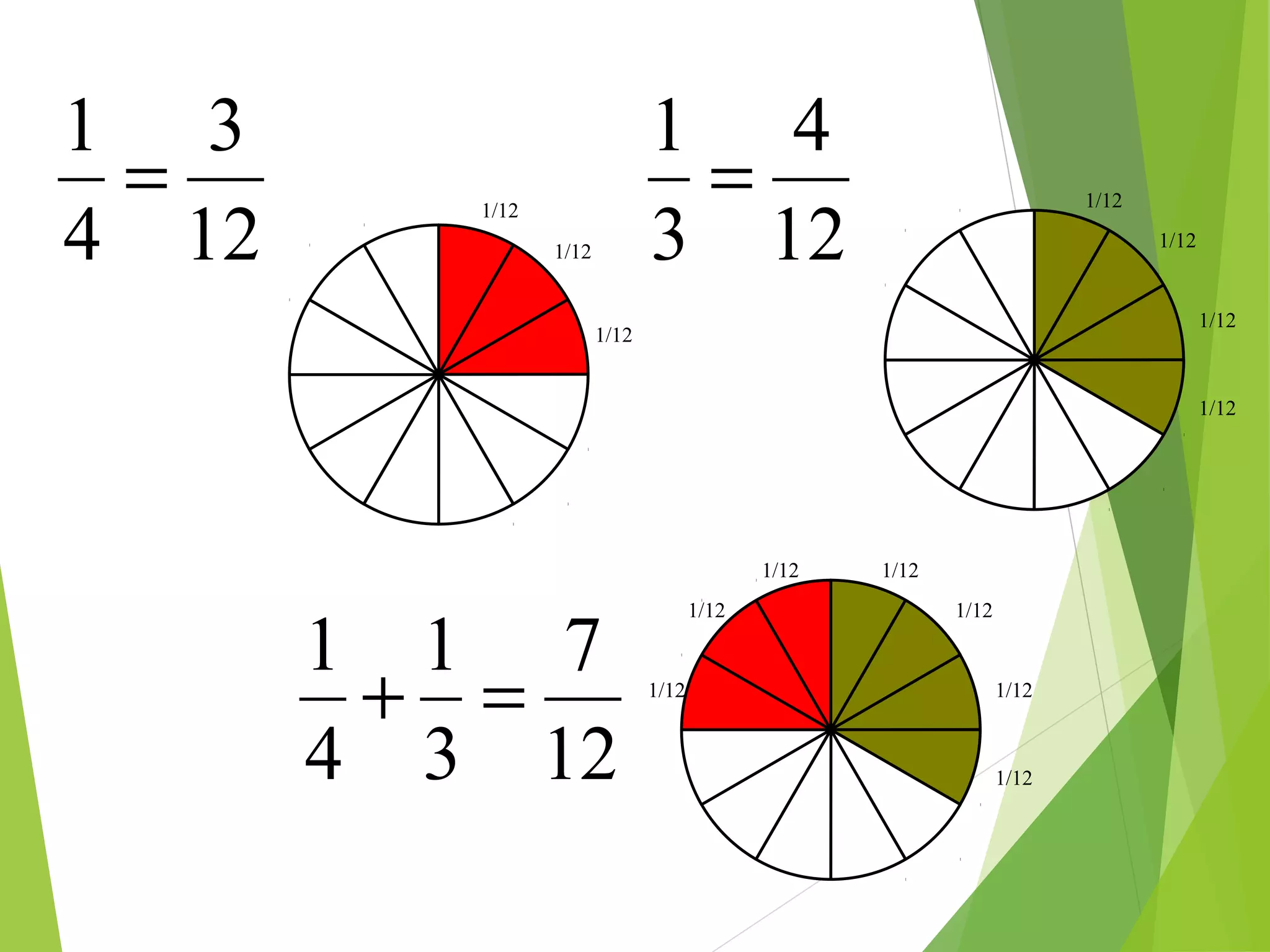
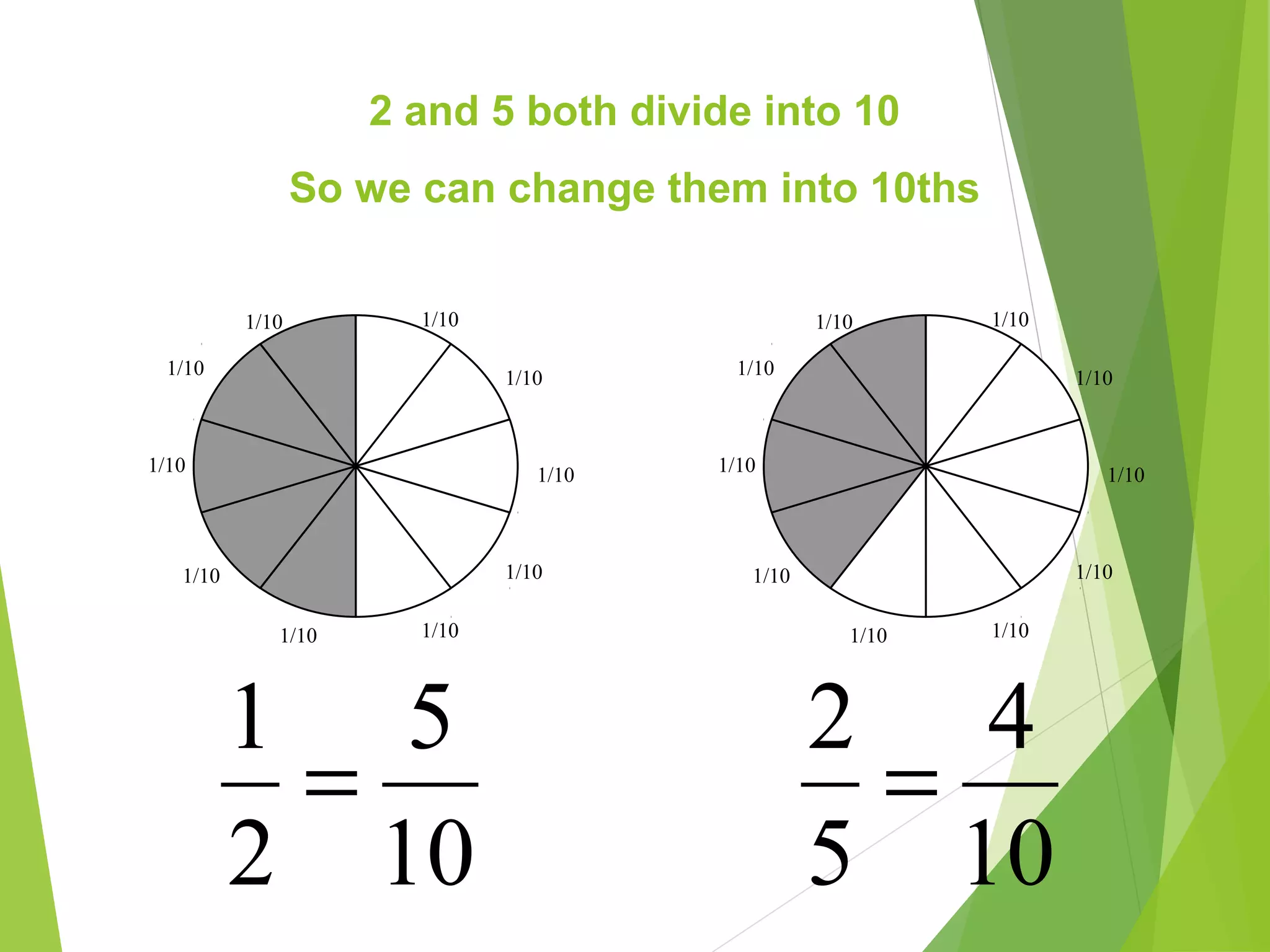
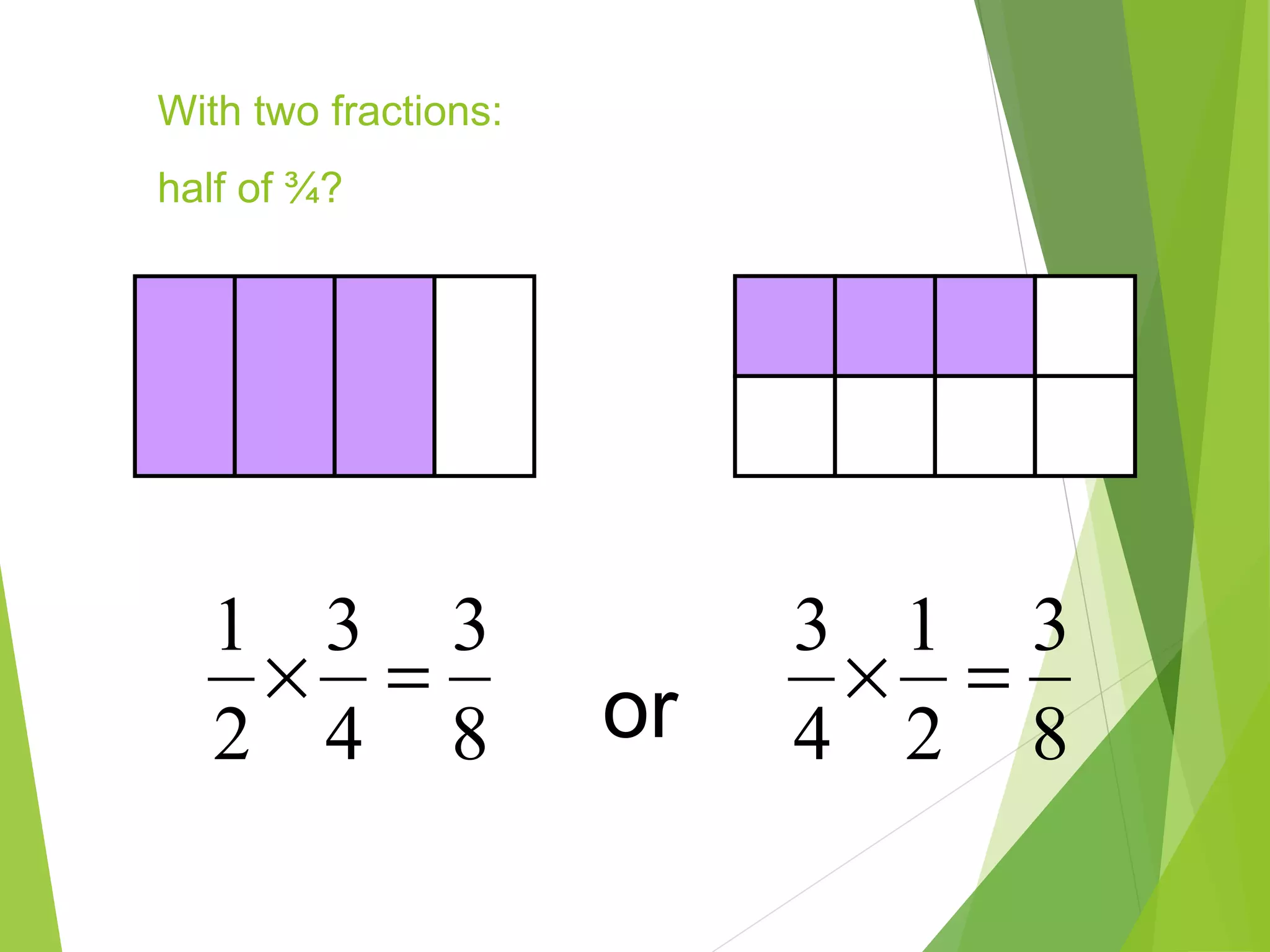
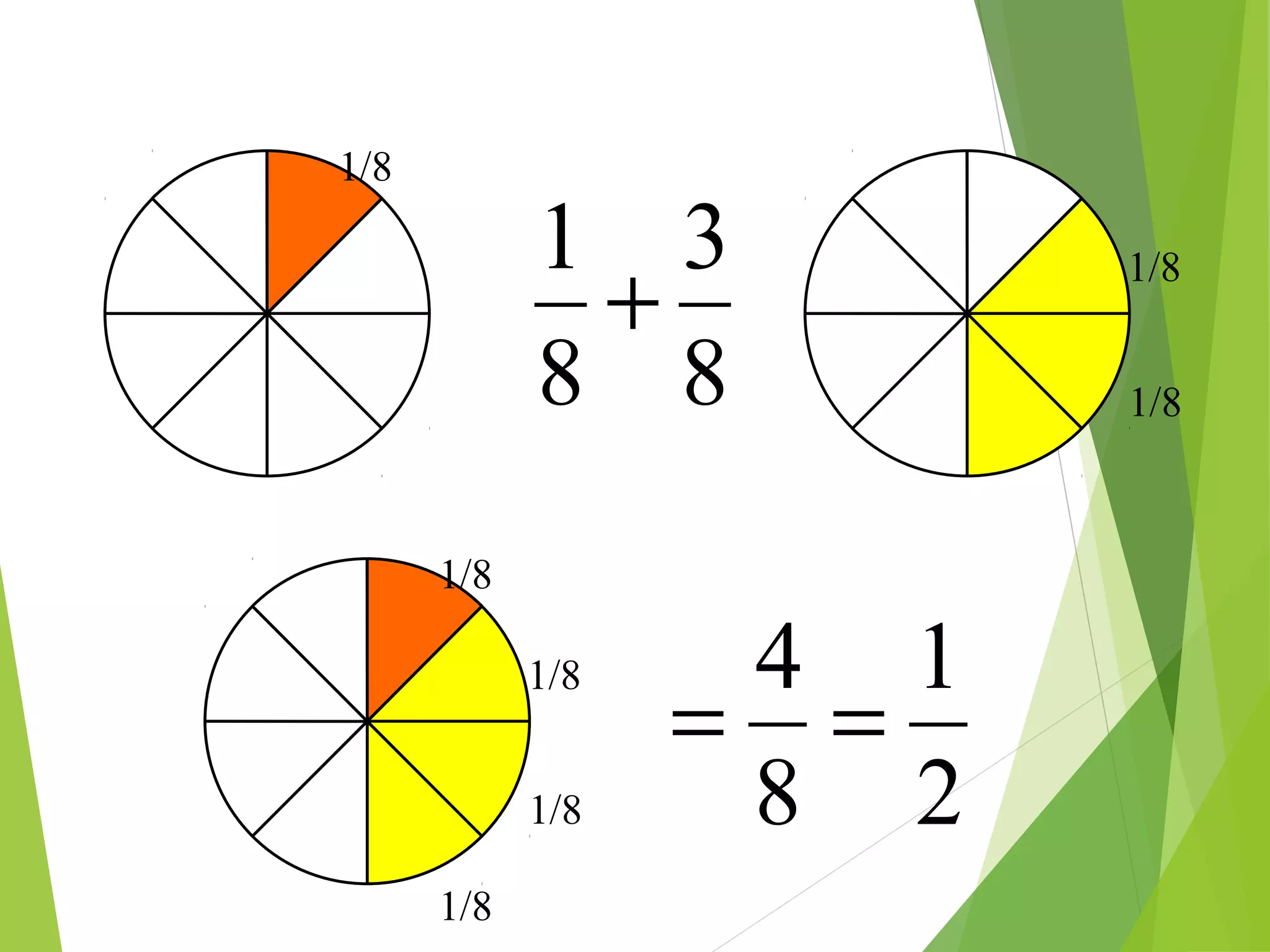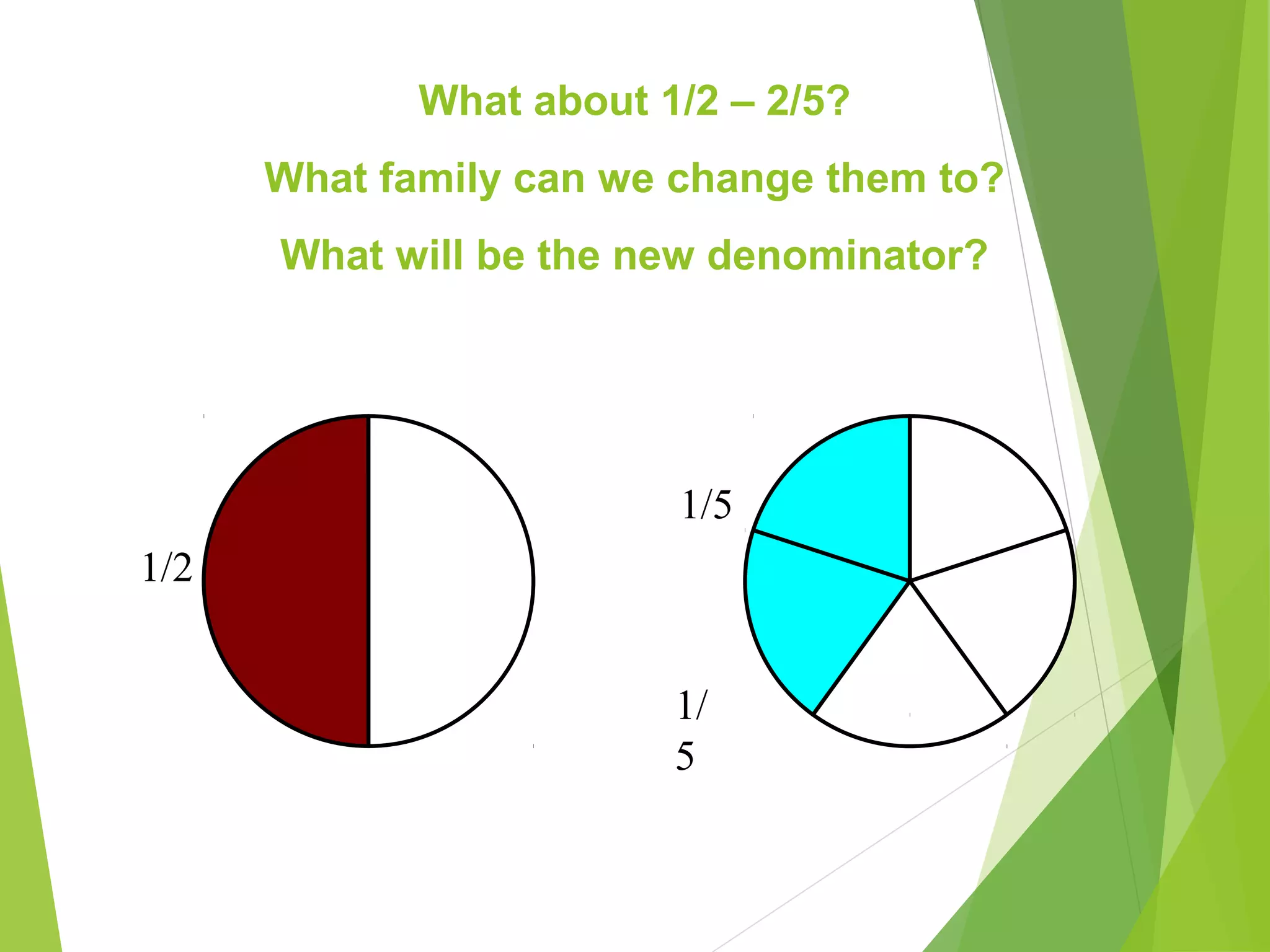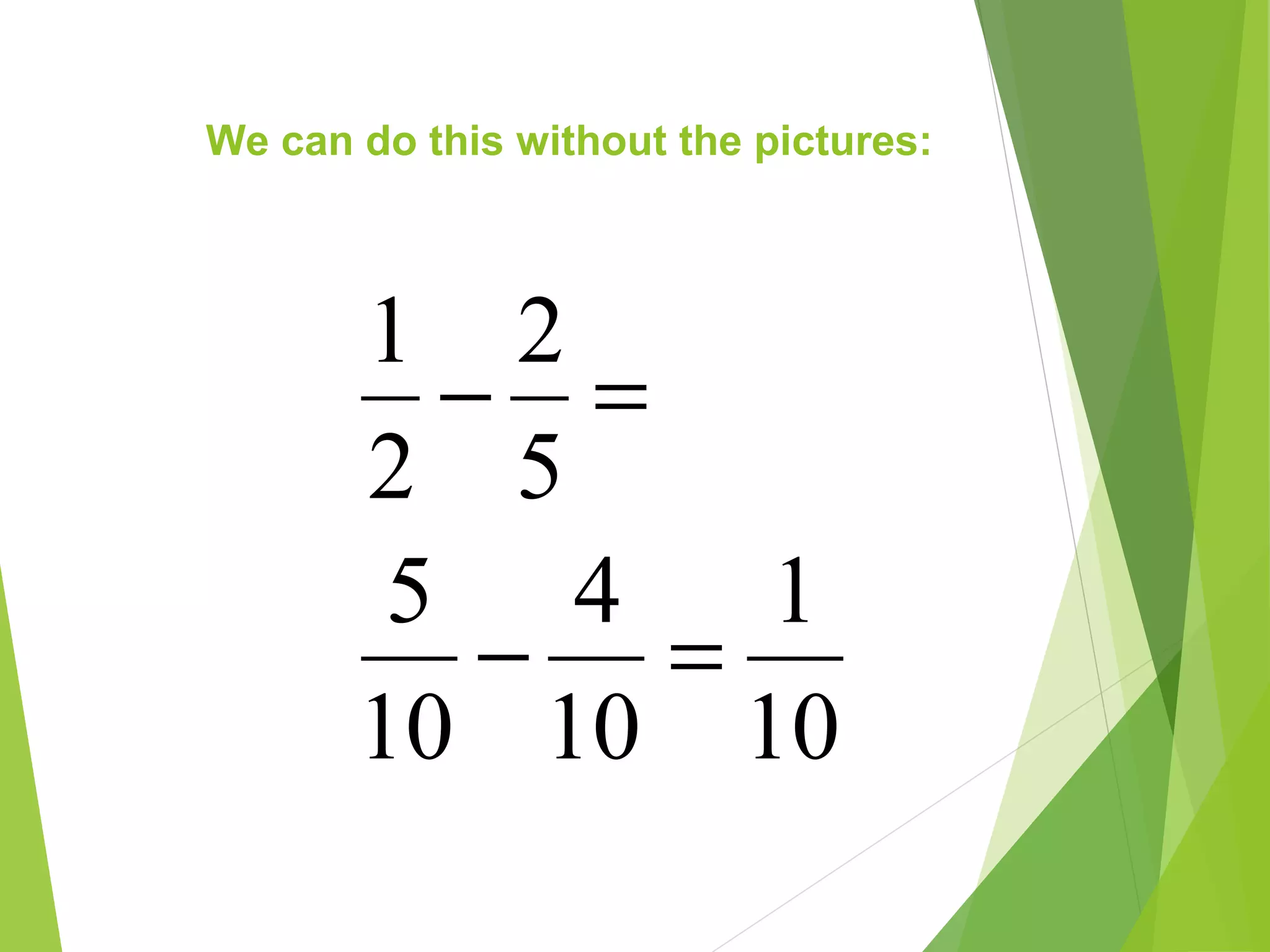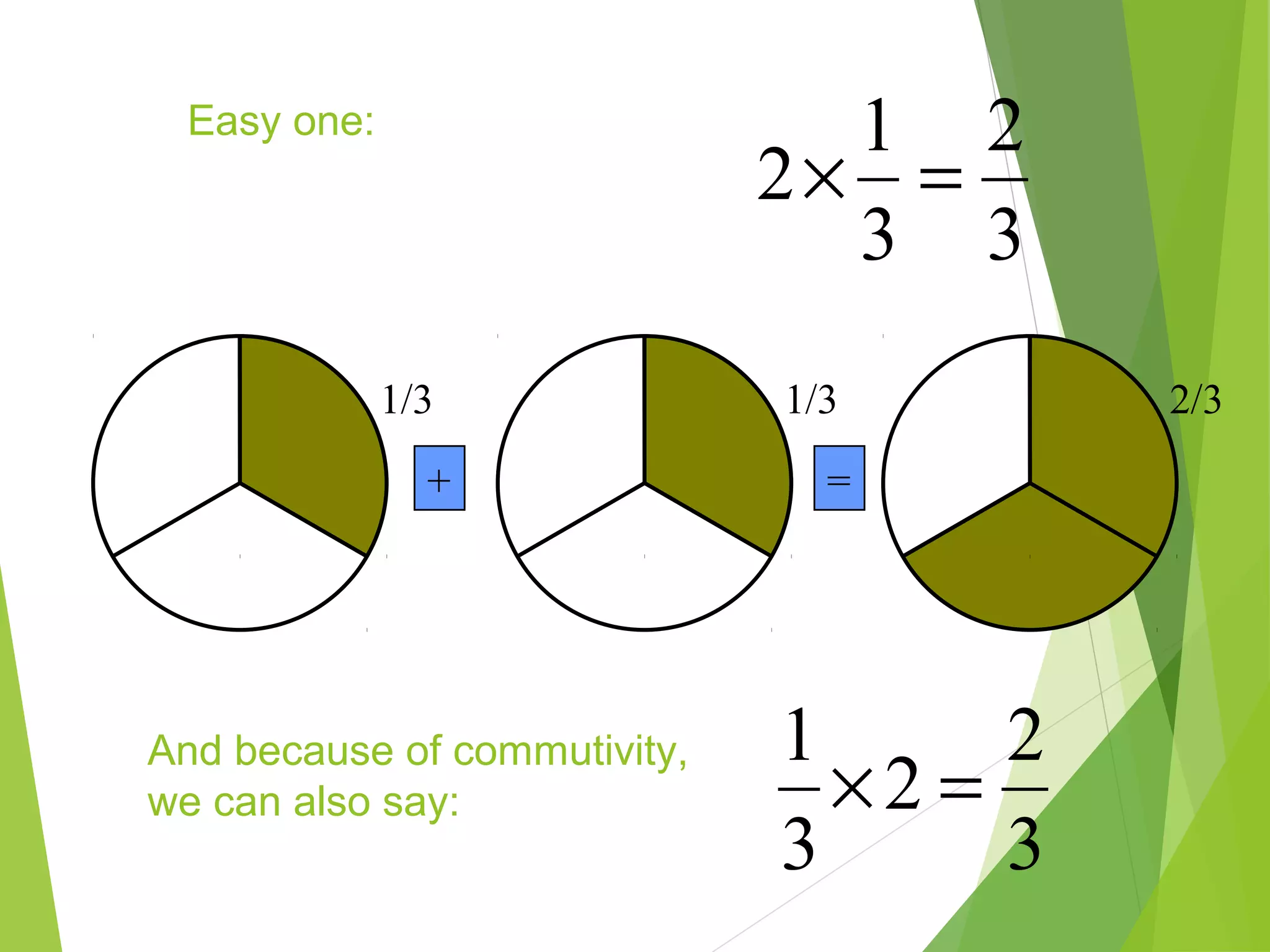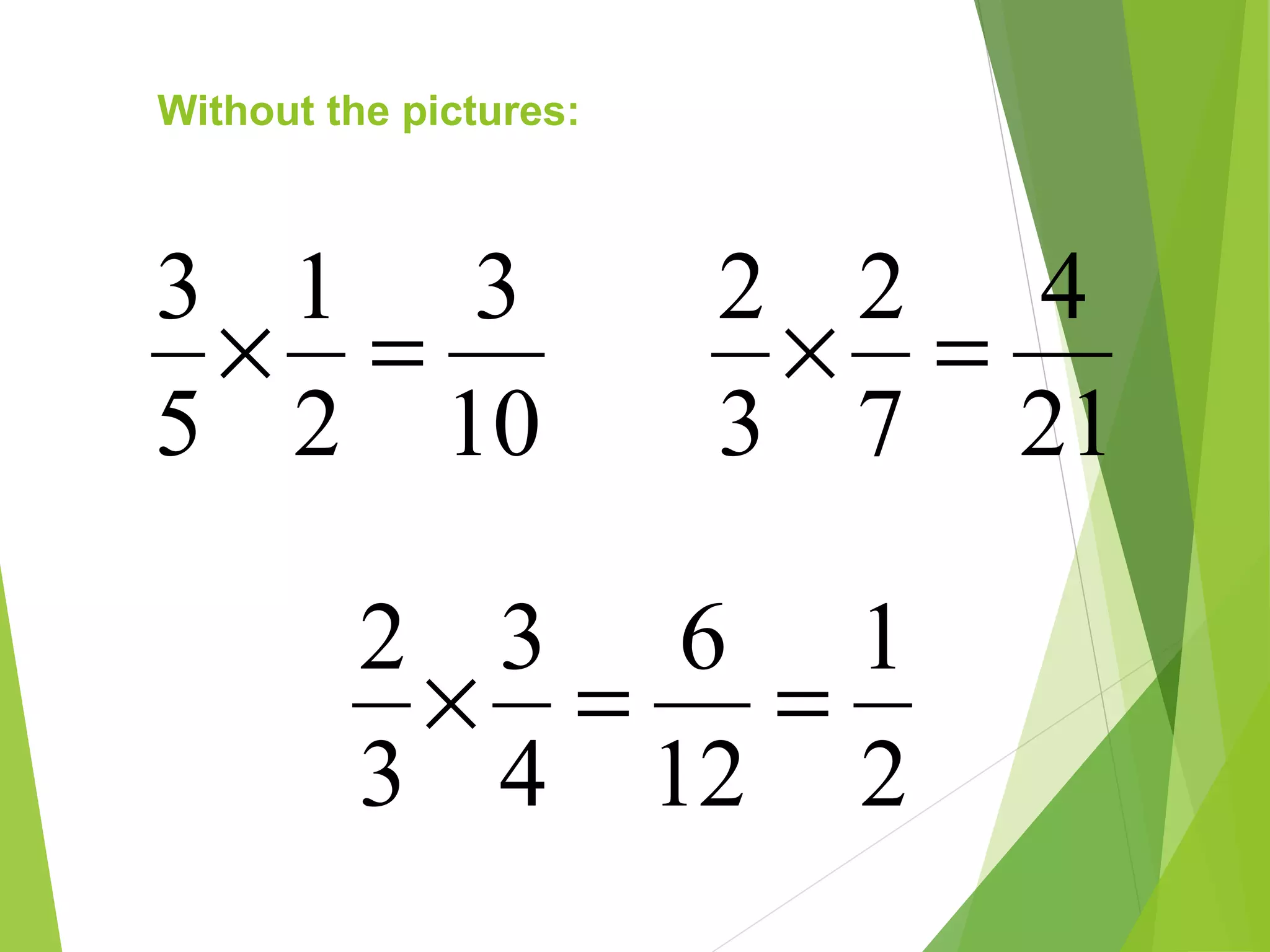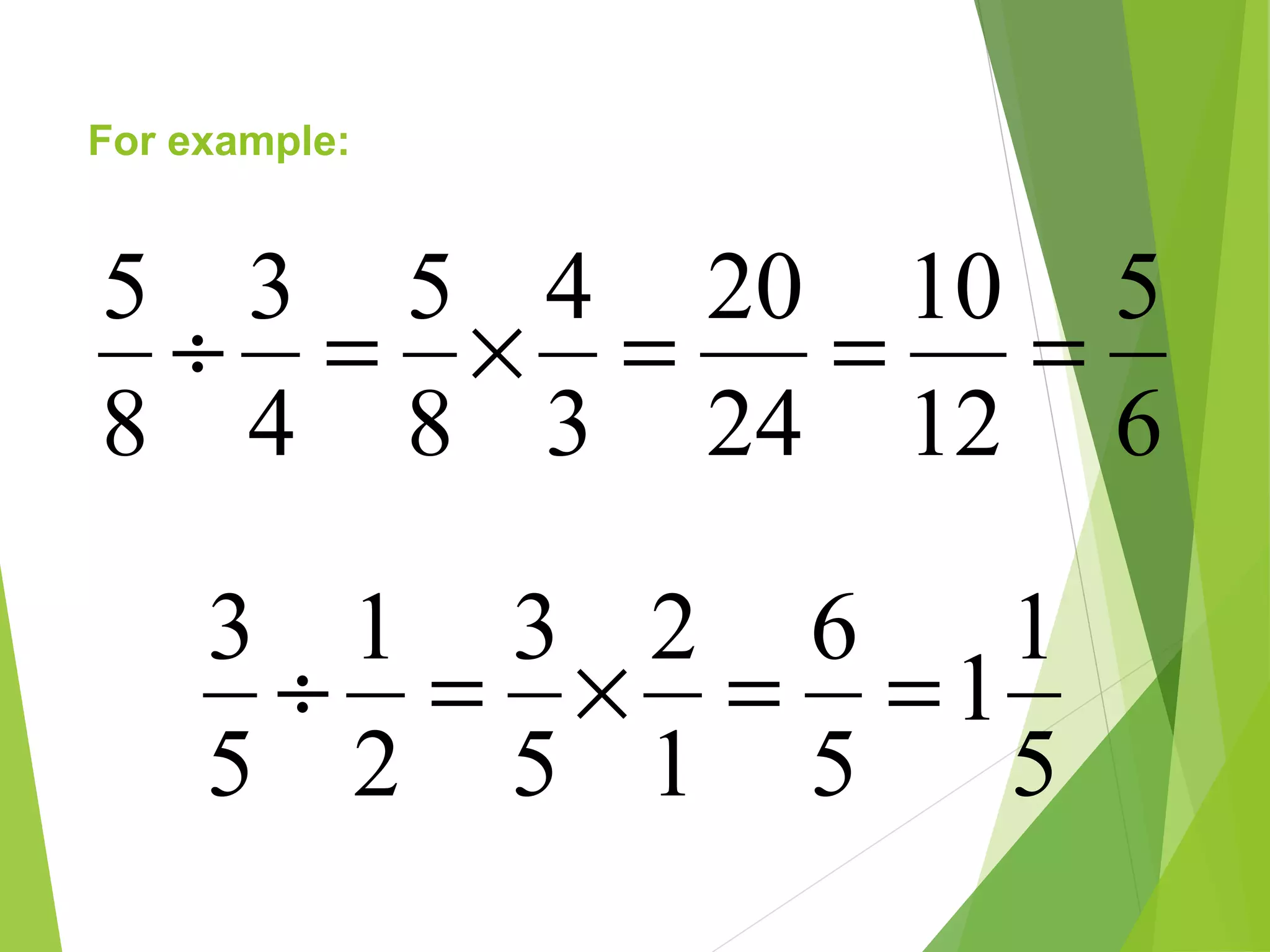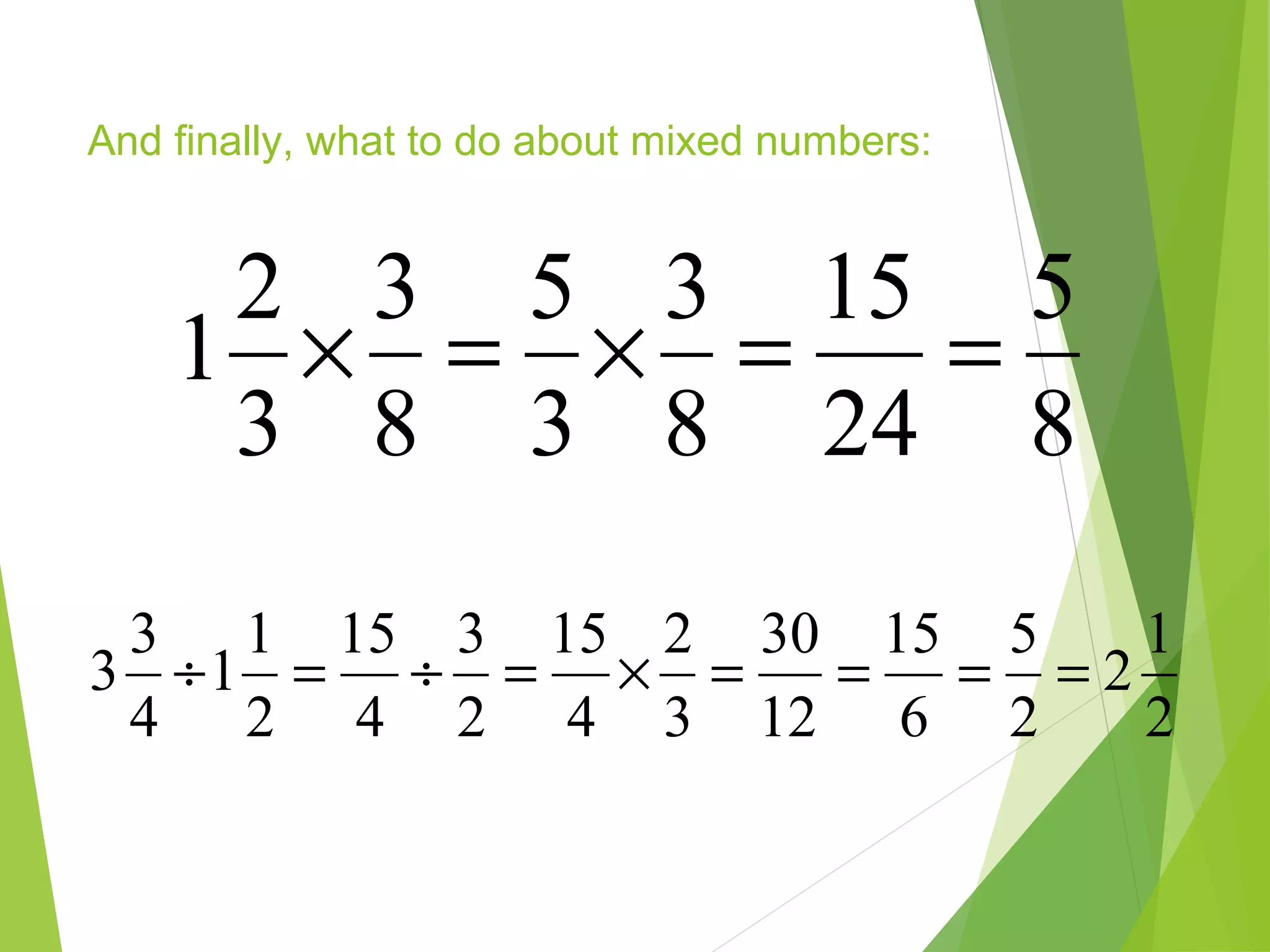This document is a PowerPoint presentation about fractions for 8th grade students. It contains definitions of key fraction terms like numerator, denominator, improper fractions, and mixed numbers. It explains how to add, subtract, multiply, and divide fractions, including using common denominators for addition and subtraction of unlike fractions. It also discusses equivalent fractions and how to determine if two fractions are equivalent using scale factors or cross-multiplication. The learning objectives are for students to understand fraction operations and how to find equivalent fractions.

1. NDHLOVU BC
PowerPoint
presentation: Fractions
Grade 8

3. WORDS TO KNOW!
 Fractions
 Whole (One)
 Unit Fractions
 Equivalent Fractions
 Numerator
 Denominator
 Common Denominator
 Improper Fractions
 Mixed Numbers

4. Learning Objective
Students will:
 Understand how to add, subtract, divide and multiply
fractions.
 Understand how to find equivalent fractions by using
multiplication and division rules.
 Compare and order fractions by identifying common
denominators and use the proper symbol. (<, >, and =)

5. MEANING OF A FRACTION
When an object is divided into equal parts, each part is
called a fraction of the object.
This circle is divided into 4 equal parts. One of
the 4 equal parts which is separated is written as
¼ and named as one-fourth.

6. Fraction has 2 numbers. Number
above the line is called
NUMERATOR and the number
below the line is called
DENOMINTOR.
Ex. In fraction 1/8 1 is numerator
and 8 is denominator.

7. What fraction of the musical instruments have
strings?
2
5

8. What fraction of the fish have stripes?
3
5

9. What fraction of the arrows
hit the bulls eye?
1
3

10. What fraction of the pins are
knocked down?
3
10

11. LIKE FRACTIONS & UNLIKE FRACTIONS
 Fractions having same denominators
are called like fractions.
 Fractions having different denominators
are called unlike fractions.

12. Improper Fractions and Mixed Numbers
An improper fraction can be converted to a
mixed number and vice versa.
3
5An improper fraction is a fraction
with the numerator larger than or
equal to the denominator.
A mixed number is a whole
number and a fraction
together.
7
3
2
Any whole number can be
transformed into an improper
fraction.
,
1
4
4 =
7
7
1=

13. Improper Fractions and Mixed Numbers
3
2
1
3
5
=
Converting improper fractions into
mixed numbers:
- divide the numerator by the denominator
- the quotient is the leading number,
- the remainder as the new numerator.
7
17
7
372
7
3
2 =
+×
=
Converting mixed
numbers into improper
fractions.
,
4
3
1
4
7
=More examples:
5
1
2
5
11
=

14. How does the denominator control a fraction?
If you share a pizza evenly among two
people, you will get
2
1
If you share a pizza evenly among
three people, you will get
3
1
If you share a pizza evenly among
four people, you will get
4
1

15. How does the denominator control a fraction?
Conclusion:
The larger the denominator the smaller the
pieces, and if the numerator is kept fixed, the
larger the denominator the smaller the fraction,
If you share a pizza evenly among
eight people, you will get only
8
1
It’s not hard to see that the slice you
get becomes smaller and smaller.
c.b
c
a
b
a
>< rwhenevei.e.

16. Addition and subtraction of Fractions
- addition means combining objects in two or
more sets
- the objects must be of the same type, i.e. we
combine bundles with bundles and sticks with
sticks.
- in fractions, we can only combine pieces of the
same size. In other words, the denominators
must be the same.

17. 5
1
5
1
+
5
2
=

18. 1/7
1/7
1/7
1/71/7
1/7
1/7
1/7
1/7
1/7
1/7
1/7
7
2
7
6
−
7
4
=

19. 1/8
1/8
1/8
1/8
1/8
1/8
1/8
8
3
8
1
+
2
1
8
4
==

20. Why were they so simple?
 Because they all had the same denominator
 They were all from the same families
What if they are of different families?

21. 1/2
1/4
4
1
2
1
+
4
3
=
Because we
know that 1/2
= 2/4

22. 1/8
1/8
1/8
1/4
1/8
1/8
1/8
1/81/8
8
5
4
1
8
3
=+
Because we
know that 1/4
= 2/8

23. But what about 1/4 + 1/3?
We can’t add, because they have
different denominators – not in the same
family.
1/4 1/3

24. What family can we change them to?
What will be the new denominator?
1/4 1/3
4 and 3 both divide into 12
So we can change them into 12ths

25. 1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
1/12
12
3
4
1
=
12
4
3
1
=
12
7
3
1
4
1
=+

26. What about 1/2 – 2/5?
What family can we change them to?
What will be the new denominator?
1/2
1/5
1/
5

27. 2 and 5 both divide into 10
So we can change them into 10ths
1/10
1/10
1/10
1/10
1/101/10
1/10
1/10
1/10
1/10 1/10
1/10
1/10
1/10
1/101/10
1/10
1/10
1/10
1/10
10
5
2
1
=
10
4
5
2
=

28. We can do this without the pictures:
10
1
10
4
10
5
5
2
2
1
=−
=−

29. Multiplication and Division

30. Easy one:
3
2
3
1
2 =×
1/3 1/3 2/3
+ =
3
2
2
3
1
=×
And because of commutivity,
we can also say:

31. With two fractions:
half of ¾?
8
3
4
3
2
1
=×
8
3
2
1
4
3
=×or

32. Without the pictures:
10
3
2
1
5
3
=×
21
4
7
2
3
2
=×
2
1
12
6
4
3
3
2
==×

33. And
division?
Unfortunately, there is no easy way to
show diagrams for division of fractions.
Nor is there any obvious way of trying to make
sense of it.
The best thing is probably just to learn the
rule!

34. To divide by a fraction
 Do not change the first fraction
 Change the division sign into a multiplication sign
 Turn the second fraction upside down
 Multiply the fractions

35. 6
5
12
10
24
20
3
4
8
5
4
3
8
5
===×=÷
For example:
5
1
1
5
6
1
2
5
3
2
1
5
3
==×=÷

36. 8
5
24
15
8
3
3
5
8
3
3
2
1 ==×=×
And finally, what to do about mixed numbers:
2
1
2
2
5
6
15
12
30
3
2
4
15
2
3
4
15
2
1
1
4
3
3 ====×=÷=÷

37. Finding Equivalent Fractions
For example
3/6 is equivalent to 10/20 because the
relationship between the numerator and the
denominator is the same in each case: 3 is
½ of 6, and 10 is ½ of 20.
Two fractions are EQUIVALENT if they are equal.
This means that the relationship between the
numerator and the denominator of one fraction is the
same as the relationship between the numerator and
denominator of the other fraction.

38. Another way you can look at it is if two fractions are
equivalent, they will have a scale factor between them.
The SCALE FACTOR is the number that you multiply
or divide the numerator and denominator in one
fraction by to get the numerator and denominator of
the second fraction.
3 9
5 15
=
x3
x3
By multiplying 3/5 by 3/3 (remember, that is the same as
multiplying by 1 whole), I will arrive at the answer 9/15.
Remember that when you are doing this you must BE
FAIR and perform the same operation to both the
numerator and the denominator.
Don’t forget that when you multiply fractions, you multiply
the numerators together and you multiply the
denominators together.

39. A third way to determine if two fractions are
equivalent is to CROSS MULTIPLY.
4 2
6 3
=
=
x
=
12
x
=
12
Multiply the numerator of one fraction by the denominator of the other.
Repeat this with the other numerator and denominator.
If the products are equal, then the fractions are equivalent.

40. Learn about and practice converting
improper fractions and mixed
numbers by clicking the objects on
this slide.

41. Click me to print a
worksheet
Practice makes perfect
Click me for a visual
demonstration
Click me to
practice.
Click us to play
fraction frenzy
Click me to play half
baked fractions on fun
brain
Click me to
watch the video

42. KEY POINTS
Remember, a fraction is an equal part of
one whole
We can split shapes, objects and
numbers into fractions
We write fractions as

43. A “View” to a Fraction
Where do you stand?

44. THANK YOU