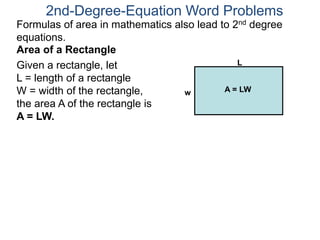
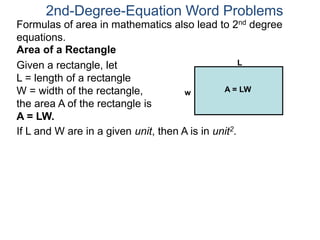
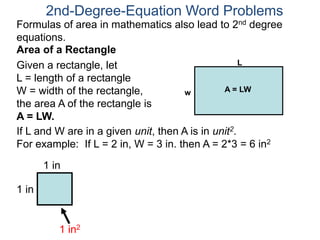
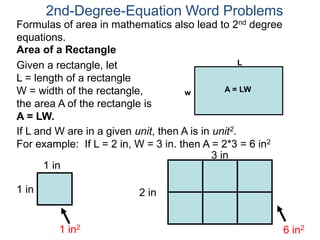
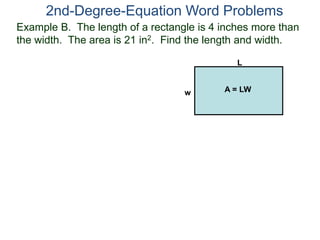
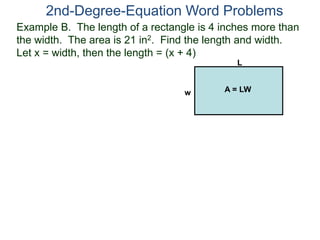
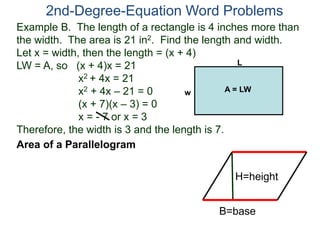
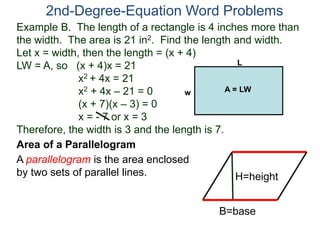
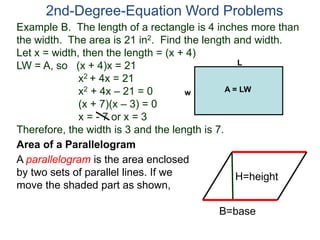
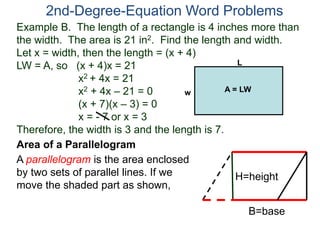
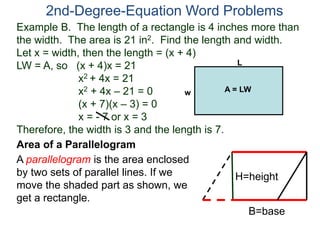
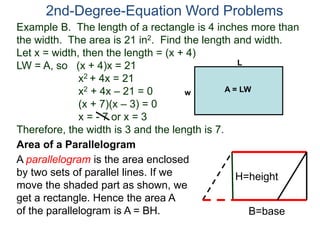
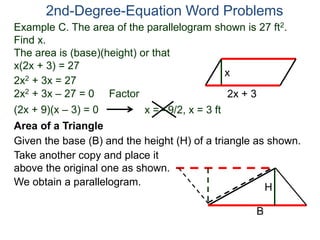
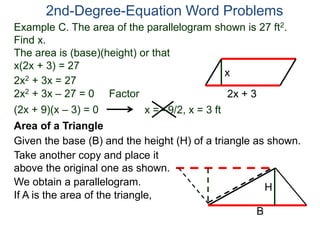
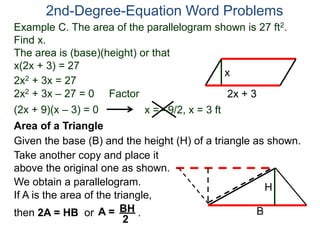
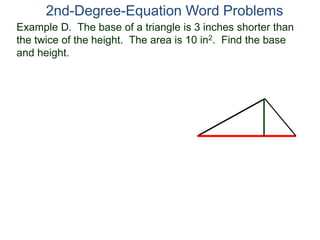
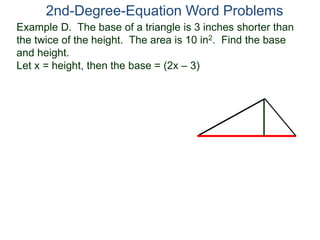
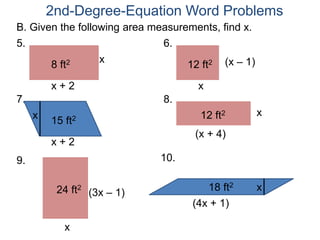
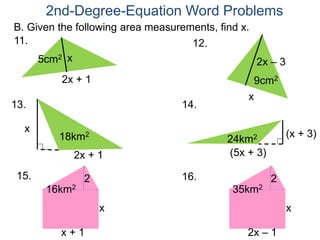
The document discusses 2nd degree equations in the context of physics and geometry word problems. It provides an example of calculating the height, time, and maximum height of a stone thrown straight up using the equation h=-16t^2 + vt. It also discusses the area formula for a rectangle, A=LW, and gives an example problem to find the length and width of a rectangle given its area is 21 in^2 and the length is 4 inches more than the width.

1. 2nd-Degree-Equation Word Problems

2. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.

3. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt

4. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt
where
h = height in feet
t = time in second
v = upward speed in feet per second

5. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt
height = -16t2 + vt
after t seconds where
h = height in feet
t = time in second
v = upward speed in feet per second

6. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt
height = -16t2 + vt
after t seconds where
h = height in feet
t = time in second
v = upward speed in feet per second
Example A. If a stone is thrown straight
up at a speed of 64 ft per second,
a. how high is it after 1 second?

7. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt
height = -16t2 + vt
after t seconds where
h = height in feet
t = time in second
v = upward speed in feet per second
Example A. If a stone is thrown straight
up at a speed of 64 ft per second,
a. how high is it after 1 second?
t = 1, v = 64,

8. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt
height = -16t2 + vt
after t seconds where
h = height in feet
t = time in second
v = upward speed in feet per second
Example A. If a stone is thrown straight
up at a speed of 64 ft per second,
a. how high is it after 1 second?
t = 1, v = 64, so
h = -16(1)2 + 64(1)

9. 2nd-Degree-Equation Word Problems
Many physics formulas are 2nd degree.
If a stone is thrown straight up on Earth then
h = -16t2 + vt
height = -16t2 + vt
after t seconds where
h = height in feet
t = time in second
v = upward speed in feet per second
Example A. If a stone is thrown straight
up at a speed of 64 ft per second,
a. how high is it after 1 second?
t = 1, v = 64, so
h = -16(1)2 + 64(1)
h = -16 + 64 = 48 ft

10. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?

11. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.

12. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.

13. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t

14. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)

15. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0

16. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4

17. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.

18. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?

19. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?
Since it takes 4 seconds for the stone to fall back to the
ground, at 2 seconds it must reach the highest point.

20. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?
Since it takes 4 seconds for the stone to fall back to the
ground, at 2 seconds it must reach the highest point.
Hence t = 2, v = 64, need to find h.

21. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?
Since it takes 4 seconds for the stone to fall back to the
ground, at 2 seconds it must reach the highest point.
Hence t = 2, v = 64, need to find h.
h = -16(2)2 + 64(2)

22. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?
Since it takes 4 seconds for the stone to fall back to the
ground, at 2 seconds it must reach the highest point.
Hence t = 2, v = 64, need to find h.
h = -16(2)2 + 64(2)
= - 64 + 128

23. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?
Since it takes 4 seconds for the stone to fall back to the
ground, at 2 seconds it must reach the highest point.
Hence t = 2, v = 64, need to find h.
h = -16(2)2 + 64(2)
= - 64 + 128
= 64 (ft)

24. 2nd-Degree-Equation Word Problems
b. How long will it take for it to fall back to the ground?
To fall back to the ground means the height h is 0.
Hence
h = 0, v = 64, need to find t.
0 = -16 t2 + 64t
0 = -16t(t – 4)
t = 0 or t – 4 = 0 or t = 4
Therefore it takes 4 seconds.
c. What is the maximum height obtained?
Since it takes 4 seconds for the stone to fall back to the
ground, at 2 seconds it must reach the highest point.
Hence t = 2, v = 64, need to find h.
h = -16(2)2 + 64(2)
= - 64 + 128
= 64 (ft)
Therefore, the maximum height is 64 feet.

25. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.

26. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle

27. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,

28. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,
the area A of the rectangle is
A = LW.

29. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,
the area A of the rectangle is
A = LW.
L
w A = LW

30. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,
the area A of the rectangle is
A = LW.
If L and W are in a given unit, then A is in unit2.
L
w A = LW

31. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,
the area A of the rectangle is
A = LW.
L
w A = LW
If L and W are in a given unit, then A is in unit2.
For example: If L = 2 in, W = 3 in. then A = 2*3 = 6 in2

32. 2nd-Degree-Equation Word Problems
Formulas of area in mathematics also lead to 2nd degree
equations.
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,
the area A of the rectangle is
A = LW.
If L and W are in a given unit, then A is in unit2.
For example: If L = 2 in, W = 3 in. then A = 2*3 = 6 in2
1 in
1 in
1 in2
L
w A = LW

33. Formulas of area in mathematics also lead to 2nd degree
equations.
If L and W are in a given unit, then A is in unit2.
For example: If L = 2 in, W = 3 in. then A = 2*3 = 6 in2
1 in
1 in
1 in2
2 in
3 in
6 in2
2nd-Degree-Equation Word Problems
Area of a Rectangle
Given a rectangle, let
L = length of a rectangle
W = width of the rectangle,
the area A of the rectangle is
A = LW.
L
w A = LW

34. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
L
w A = LW

35. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
L
w A = LW

36. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
L
w A = LW

37. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
L
w A = LW

38. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
L
w A = LW

39. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
L
w A = LW

40. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
L
w A = LW

41. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
L
w A = LW

42. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
Therefore, the width is 3 and the length is 7.
L
w A = LW

43. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
w A = LW
Therefore, the width is 3 and the length is 7.
Area of a Parallelogram
L
H=height
B=base

44. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
w A = LW
Therefore, the width is 3 and the length is 7.
Area of a Parallelogram
A parallelogram is the area enclosed
by two sets of parallel lines.
L
H=height
B=base

45. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
w A = LW
Therefore, the width is 3 and the length is 7.
Area of a Parallelogram
A parallelogram is the area enclosed
by two sets of parallel lines. If we
move the shaded part as shown,
L
H=height
B=base

46. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
Therefore, the width is 3 and the length is 7.
Area of a Parallelogram
A parallelogram is the area enclosed
by two sets of parallel lines. If we
move the shaded part as shown,
H=height
B=base
L
w A = LW

47. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
Therefore, the width is 3 and the length is 7.
Area of a Parallelogram
A parallelogram is the area enclosed
by two sets of parallel lines. If we
move the shaded part as shown, we
get a rectangle.
H=height
B=base
L
w A = LW

48. 2nd-Degree-Equation Word Problems
Example B. The length of a rectangle is 4 inches more than
the width. The area is 21 in2. Find the length and width.
Let x = width, then the length = (x + 4)
LW = A, so (x + 4)x = 21
x2 + 4x = 21
x2 + 4x – 21 = 0
(x + 7)(x – 3) = 0
x = - 7 or x = 3
Therefore, the width is 3 and the length is 7.
Area of a Parallelogram
A parallelogram is the area enclosed
by two sets of parallel lines. If we
move the shaded part as shown, we
get a rectangle. Hence the area A
of the parallelogram is A = BH.
H=height
B=base
L
w A = LW

49. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
x
2x + 3

50. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
2x + 3
2x2 + 3x = 27

51. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0

52. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0

53. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft

54. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft

55. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
Area of a Triangle
x
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft

56. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft
Area of a Triangle
Given the base (B) and the height (H) of a triangle as shown.
B
H

57. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
Area of a Triangle
Given the base (B) and the height (H) of a triangle as shown.
B
H
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft
Take another copy and place it
above the original one as shown .

58. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
Area of a Triangle
Given the base (B) and the height (H) of a triangle as shown.
B
H
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft
Take another copy and place it
above the original one as shown.

59. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
Area of a Triangle
Given the base (B) and the height (H) of a triangle as shown.
B
H
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft
Take another copy and place it
above the original one as shown.
We obtain a parallelogram.

60. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
Area of a Triangle
Given the base (B) and the height (H) of a triangle as shown.
B
H
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft
Take another copy and place it
above the original one as shown.
We obtain a parallelogram.
If A is the area of the triangle,

61. 2nd-Degree-Equation Word Problems
Example C. The area of the parallelogram shown is 27 ft2.
Find x.
The area is (base)(height) or that
x(2x + 3) = 27
x
Area of a Triangle
Given the base (B) and the height (H) of a triangle as shown.
B
H
2x + 3
2x2 + 3x = 27
2x2 + 3x – 27 = 0 Factor
(2x + 9)(x – 3) = 0 x = –9/2, x = 3 ft
Take another copy and place it
above the original one as shown.
We obtain a parallelogram.
If A is the area of the triangle,
then 2A = HB or A = B H .
2

62. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.

63. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.

64. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)

65. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
x
2x– 3

66. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
x
2x– 3

67. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
20 = 2x2 – 3x
x
2x– 3

68. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
20 = 2x2 – 3x
0 = 2x2 – 3x – 20
x
2x– 3

69. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
20 = 2x2 – 3x
0 = 2x2 – 3x – 20
x
0 = (x – 4)(2x + 5)
2x– 3

70. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
20 = 2x2 – 3x
0 = 2x2 – 3x – 20
x
0 = (x – 4)(2x + 5)
x = 4 or x = -5/2
2x– 3

71. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
20 = 2x2 – 3x
0 = 2x2 – 3x – 20
x
0 = (x – 4)(2x + 5)
x = 4 or x = -5/2
2x– 3

72. 2nd-Degree-Equation Word Problems
Example D. The base of a triangle is 3 inches shorter than
the twice of the height. The area is 10 in2. Find the base
and height.
Let x = height, then the base = (2x – 3)
Hence, use the formula 2A = BH
2*10 = (2x – 3) x
20 = 2x2 – 3x
0 = 2x2 – 3x – 20
x
0 = (x – 4)(2x + 5)
x = 4 or x = -5/2
2x– 3
Therefore the height is 4 in. and the base is 5 in.

73. 2nd-Degree-Equation Word Problems
Exercise A. Use the formula h = –16t2 + vt for the following
problems.
1. A stone is thrown upward at a speed of v = 64 ft/sec,
how long does it take for it’s height to reach 48 ft?
2. A stone is thrown upward at a speed of v = 64 ft/sec,
how long does it take for it’s height to reach 28 ft?
3. A stone is thrown upward at a speed of v = 96 ft/sec,
a. how long does it take for its height to reach 80 ft? Draw a
picture.
b. how long does it take for its height to reach the highest
point?
c. What is the maximum height it reached?
4. A stone is thrown upward at a speed of v = 128 ft/sec,
a. how long does it take for its height to reach 256 ft?
Draw a picture. How long does it take for its height to reach
the highest point and what is the maximum height it reached?

74. 2nd-Degree-Equation Word Problems
B. Given the following area measurements, find x.
5.
8 ft2
x + 2
x
6.
12 ft2
x
(x – 1)
7.
x + 2
8.
12 ft2 x
(x + 4)
9.
24 ft2
(3x – 1)
x
10.
15 ft x 2
18 ft2 x
(4x + 1)

75. 2nd-Degree-Equation Word Problems
B. Given the following area measurements, find x.
2x + 1
11.
5cm2 x
12.
2x – 3
9cm2
x
2x + 1
13.
x
18km2
14.
(x + 3)
24km2
(5x + 3)
15. 16.
16km2
2
x
x + 1
35km2
2
x
2x – 1