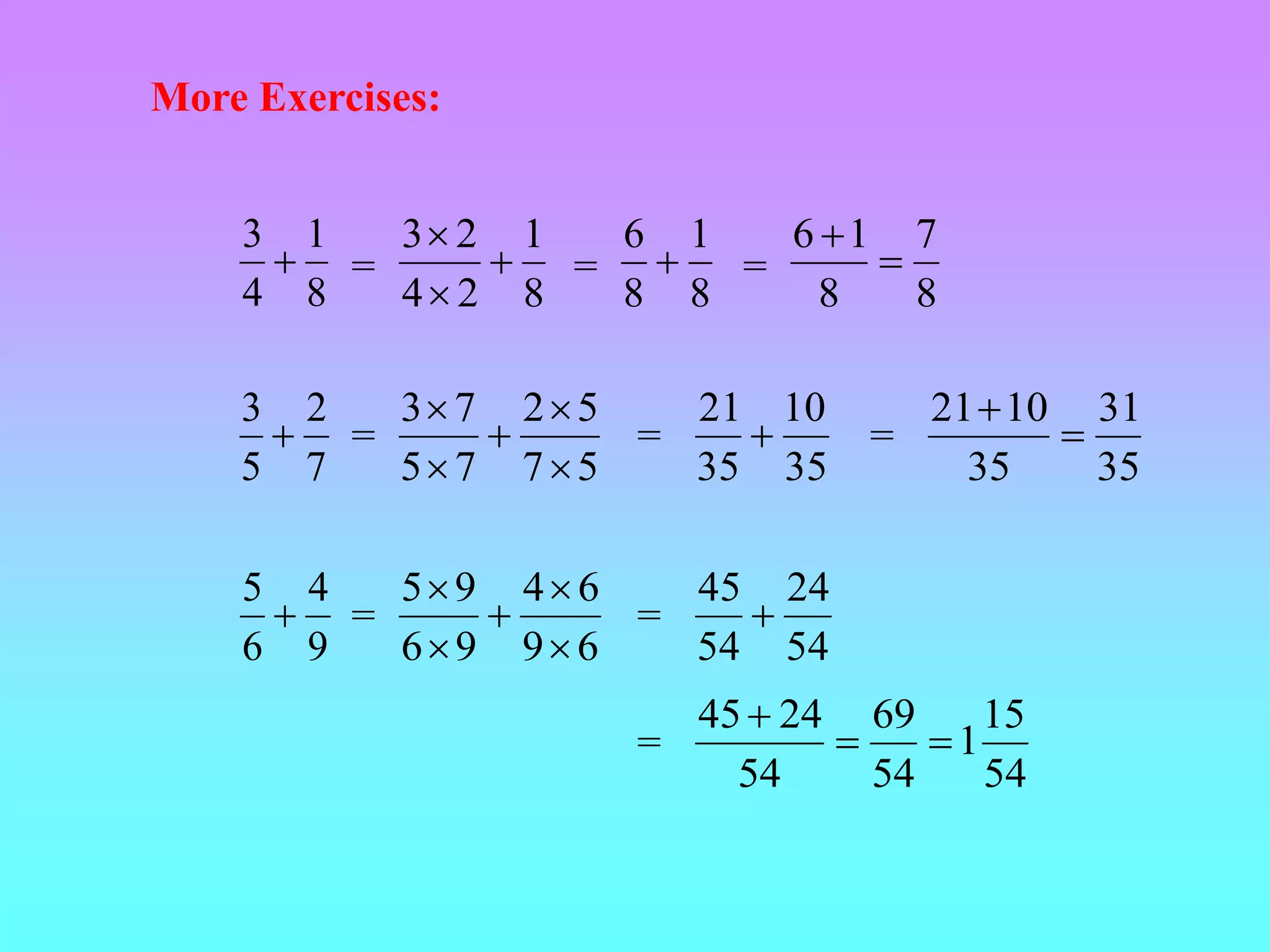This document contains notes and examples about fractions. It begins by defining fractions and the different types, including proper fractions, improper fractions, and mixed numbers. It discusses how the numerator and denominator affect the size of a fraction. It also covers equivalent fractions, comparing fractions, and operations like addition and subtraction on fractions with equal or different denominators. Examples are provided for changing between improper fractions and mixed numbers, reducing fractions to lowest terms, and performing calculations on fractions.