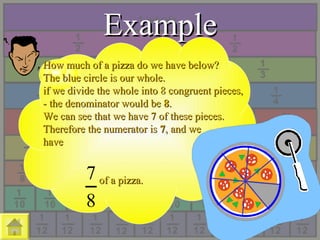
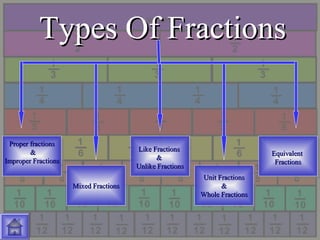
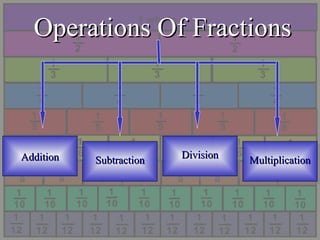
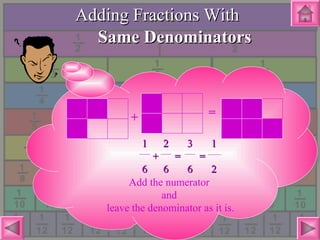
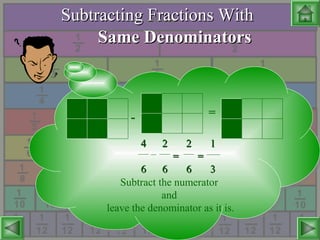
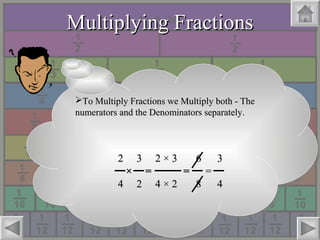
The document discusses fractions, including: - What fractions are and examples of fractions - The parts of a fraction including the numerator and denominator - Different types of fractions such as proper, improper, mixed, equivalent and unit fractions - How to perform operations on fractions including addition, subtraction, multiplication and division - How to compare and convert between different types of fractions

1. Fractions

2. IndexIndex
1.1. What are FractionsWhat are Fractions
2.2. ExamplesExamples
3.3. Need of FractionsNeed of Fractions
4.4. Parts of FractionsParts of Fractions
5.5. ExampleExample
6.6. Types of Fractions-Types of Fractions-
 Proper fractions & Improper FractionsProper fractions & Improper Fractions
 Mixed FractionsMixed Fractions
 Like Fractions & Unlike FractionsLike Fractions & Unlike Fractions
 Equivalent FractionsEquivalent Fractions
7.7. Operations of FractionsOperations of Fractions
 AdditionAddition
 SubtractionSubtraction
 MultiplicationMultiplication
 DivisionDivision
8.8. ComparisonComparison
 Greater than and SmallerGreater than and Smaller
thanthan
 How does the DenominatorHow does the Denominator
controls the Fractioncontrols the Fraction
 How does the DenominatorHow does the Denominator
controls the Fractioncontrols the Fraction

3. What are Fractions?What are Fractions?
Fractions are for counting part of something.Fractions are for counting part of something.
Loosely speaking, a fraction is a quantity that cannot beLoosely speaking, a fraction is a quantity that cannot be
represented by a whole number.represented by a whole number.
A fraction (from the Latin fractus, broken) is a number thatA fraction (from the Latin fractus, broken) is a number that
can represent part of a whole. The earliest fractions werecan represent part of a whole. The earliest fractions were
reciprocals of integers: ancient symbols representing one partreciprocals of integers: ancient symbols representing one part
of two, one part of three, one part of four, and so on. A muchof two, one part of three, one part of four, and so on. A much
later development were the common or "vulgar" fractionslater development were the common or "vulgar" fractions
which are still used today (½, ⅝, ¾, etc.)which are still used today (½, ⅝, ¾, etc.)

4. 11 22
//101011
//1212
11
//88
11 ½½
1111
//1212
5555
//6060
ExamplesExamples

5. Need Of Fractions?Need Of Fractions?
Consider the following scenario.Consider the following scenario.
Can you finish the whole cake?Can you finish the whole cake?
If not, how many cakes did you eat?If not, how many cakes did you eat?
1 is not the answer, neither is 0.1 is not the answer, neither is 0.
This suggest that we need a newThis suggest that we need a new
kind of number i.e.kind of number i.e. FractionFraction..

6. b
a
Parts Of Fractions?Parts Of Fractions?
I’m the NUMERATOR.I’m the NUMERATOR.
I tell you the number of partsI tell you the number of parts
I’m the DENOMINATOR.I’m the DENOMINATOR.
I tell you the name of partI tell you the name of part
TheThe denominatordenominator tells us howtells us how
many congruent pieces the whole ismany congruent pieces the whole is
divided into, thus this number cannotdivided into, thus this number cannot
be 0. (b)be 0. (b)
TheThe numeratornumerator tells us how manytells us how many
such pieces are being considered. (a)such pieces are being considered. (a)

7. ExampleExample
8
7
How much of a pizza do we have below?How much of a pizza do we have below?
The blue circle is our whole.The blue circle is our whole.
if we divide the whole into 8 congruent pieces,if we divide the whole into 8 congruent pieces,
- the denominator would be- the denominator would be 88..
We can see that we have 7 of these pieces.We can see that we have 7 of these pieces.
Therefore the numerator isTherefore the numerator is 77, and we, and we
havehave
of a pizza.of a pizza.

8. Proper fractionsProper fractions
&&
Improper FractionsImproper Fractions
Proper fractionsProper fractions
&&
Improper FractionsImproper Fractions
EquivalentEquivalent
FractionsFractions
EquivalentEquivalent
FractionsFractions
Like FractionsLike Fractions
&&
Unlike FractionsUnlike Fractions
Like FractionsLike Fractions
&&
Unlike FractionsUnlike Fractions
Mixed FractionsMixed FractionsMixed FractionsMixed Fractions
Unit FractionsUnit Fractions
&&
Whole FractionsWhole Fractions
Unit FractionsUnit Fractions
&&
Whole FractionsWhole Fractions
Types Of FractionsTypes Of Fractions

9. In Proper Fractions theIn Proper Fractions the
numerator is less than thenumerator is less than the
denominator.denominator.
E.g.. – 1/2 ,3/4 ,2/7 etc.E.g.. – 1/2 ,3/4 ,2/7 etc.
In Proper Fractions theIn Proper Fractions the
numerator is less than thenumerator is less than the
denominator.denominator.
E.g.. – 1/2 ,3/4 ,2/7 etc.E.g.. – 1/2 ,3/4 ,2/7 etc. 11
44
In Improper Fractions theIn Improper Fractions the
numerator is greater than (ornumerator is greater than (or
equal to)equal to) the denominator.the denominator.
E.g. – 4/2 ,9/5 ,6/6 etc.E.g. – 4/2 ,9/5 ,6/6 etc.
Every whole no is ImproperEvery whole no is Improper
FractionFraction
E.g. – 24 = 24/1E.g. – 24 = 24/1
In Improper Fractions theIn Improper Fractions the
numerator is greater than (ornumerator is greater than (or
equal to)equal to) the denominator.the denominator.
E.g. – 4/2 ,9/5 ,6/6 etc.E.g. – 4/2 ,9/5 ,6/6 etc.
Every whole no is ImproperEvery whole no is Improper
FractionFraction
E.g. – 24 = 24/1E.g. – 24 = 24/1
77
44
ProperProper && ImproperImproper FractionsFractions
I’m SmallerI’m Smaller
I’m BiggerI’m Bigger

10. 1 ¾1 ¾ 7/87/8
Mixed FractionsMixed Fractions
In Mixed Fractions a whole numberIn Mixed Fractions a whole number
and a proper fraction are together.and a proper fraction are together.
E.g.. –2 1/4, 16 2/5 etc.E.g.. –2 1/4, 16 2/5 etc.
Mixed Fractions and ImproperMixed Fractions and Improper
Fractions are same.Fractions are same.
We can use any to show the sameWe can use any to show the same
amount.amount.
==

11. ConversionConversion
8
1
9
8
1
9 1
= 1
8 8
7
17
7
372
7
3
2 =
+×
=
ImproperImproper FractionFraction toto MixedMixed FractionFraction
divide the numerator by the denominator thedivide the numerator by the denominator the
quotient is the leading number, the remainder asquotient is the leading number, the remainder as
the new numerator.the new numerator.
MixedMixed Fraction to Improper FractionFraction to Improper Fraction
multiply the whole number with the denominatormultiply the whole number with the denominator
and add the numerator to it. The answer is theand add the numerator to it. The answer is the
numerator and the denominator is samenumerator and the denominator is same

12. LikeLike && UnlikeUnlike FractionsFractions
In Like Fractions the denominators ofIn Like Fractions the denominators of
the Fractions are samethe Fractions are same
In Unlike Fractions the denominatorsIn Unlike Fractions the denominators
of the Fractions are different.of the Fractions are different.

13. Unit FractionsUnit Fractions &&
Whole FractionsWhole Fractions
In Unit Fractions theIn Unit Fractions the
numerator of thenumerator of the
Fraction is 1.Fraction is 1.
In Whole Fractions theIn Whole Fractions the
denominators of the Fraction isdenominators of the Fraction is
1.1.

14. Convert Unlike Fractions to LikeConvert Unlike Fractions to Like
FractionsFractions
 Simplify all the Fractions.Simplify all the Fractions.
 Find LCM of all the Denominators.Find LCM of all the Denominators.
 Multiply all the fractions with a special form of 1Multiply all the fractions with a special form of 1
to get 84 (here). Now these are Like Fractions.to get 84 (here). Now these are Like Fractions.
3 5 43 5 4
4 3 74 3 7
, ,
4,3,74,3,7
2,3,72,3,7
1,3,71,3,7
1,1,71,1,7
1,1,11,1,1
22
2
3
7
2 2 3 7 = 842 2 3 7 = 84×× ×
63 113 4863 113 48
84 84 8484 84 84
, ,
==

15. Equivalent FractionsEquivalent Fractions
They are the fractions that may have many differentThey are the fractions that may have many different
appearances, but are same.appearances, but are same.
In the following picture we have ½ of a cake as theIn the following picture we have ½ of a cake as the
cake is divided into two congruent parts and we havecake is divided into two congruent parts and we have
only one of those parts.only one of those parts.
But if we cut the cake into smaller congruentBut if we cut the cake into smaller congruent
pieces, we can see thatpieces, we can see that
½ = 2/4 = 4/8 = 3/6½ = 2/4 = 4/8 = 3/6

16. Equivalent FractionsEquivalent Fractions
To know that two or more Fractions areTo know that two or more Fractions are
Equivalent we must simplify (change to its lowestEquivalent we must simplify (change to its lowest
term) them.term) them.
Simplify: A fraction is in its lowest terms (or isSimplify: A fraction is in its lowest terms (or is
reduced) if we cannot find a whole number (otherreduced) if we cannot find a whole number (other
than 1) that can divide into both its numerator andthan 1) that can divide into both its numerator and
denominator.denominator.
E.g.- 5 : 5 & 10 can be divided by 5. 5 1E.g.- 5 : 5 & 10 can be divided by 5. 5 1
10 10 210 10 2

17. ExampleExample
Are 14 & 30 equal ?
21 45
2 = 2 14 = 30
3 3 21 45
reduce
3
2
721
714 =
÷
÷14
21
reduce
3
2
1545
1530 =
÷
÷30
45

18. Making Equivalent FractionsMaking Equivalent Fractions
To make Equivalent Fractions we multiply theTo make Equivalent Fractions we multiply the
Fraction with a special form of 1 (same numerator &Fraction with a special form of 1 (same numerator &
denominator- 4/4, 10/10 etc.)denominator- 4/4, 10/10 etc.)
E.g. : 4 = 4 5 = 20E.g. : 4 = 4 5 = 20
5 5 5 255 5 5 25
×
×

19. Operations Of FractionsOperations Of Fractions
SubtractionSubtractionSubtractionSubtraction MultiplicationMultiplicationMultiplicationMultiplicationAdditionAdditionAdditionAddition DivisionDivisionDivisionDivision

20. Addition Of FractionsAddition Of Fractions
Things To Know !!!!Things To Know !!!!
 SimplifyingSimplifying
 Like and Unlike FractionsLike and Unlike Fractions
 Like fractions are Compulsory to add.Like fractions are Compulsory to add.
 If there are Unlike Fractions then convert them to likeIf there are Unlike Fractions then convert them to like
fractions.fractions.
 The Denominator should not be added.The Denominator should not be added.
 Always change Improper fraction to a mixedAlways change Improper fraction to a mixed
fraction.fraction.

21. Adding FractionsAdding Fractions
Addition means combining objects in two or moreAddition means combining objects in two or more
setssets
The objects must be of the same type, i.e. weThe objects must be of the same type, i.e. we
combine bundles with bundles and sticks with sticks.combine bundles with bundles and sticks with sticks.
In fractions, we can only combine pieces of theIn fractions, we can only combine pieces of the
same size. In other words, the denominators must besame size. In other words, the denominators must be
the same.the same.

22. Adding Fractions WithAdding Fractions With
Same DenominatorsSame Denominators
+ =
Add the numerator
and
leave the denominator as it is.
1 2 3 11 2 3 1
+ = =+ = =
6 6 6 26 6 6 2

23. Adding Fractions withAdding Fractions with
Different DenominatorsDifferent Denominators
If there are different denominators in theIf there are different denominators in the
fractions, then we change them to likefractions, then we change them to like
fractions.fractions.
15
5
3
1
= =
5
2
15
65
2
3
1
+
15
11
15
6
15
5
5
2
3
1
=+=+

24. Adding Mixed FractionsAdding Mixed Fractions
Change the Mixed fractions toChange the Mixed fractions to
Improper Fractions and then toImproper Fractions and then to
Like Fractions.Like Fractions.
At last add the Improper LikeAt last add the Improper Like
Fractions.Fractions.
Don’t forget to change theDon’t forget to change the
answer to Mixed Fraction again.answer to Mixed Fraction again.

25. Subtraction Of FractionsSubtraction Of Fractions
Things To Know !!!!Things To Know !!!!
 SimplifyingSimplifying
 Like and Unlike FractionsLike and Unlike Fractions
 Like fractions are Compulsory to subtract.Like fractions are Compulsory to subtract.
 If there are Unlike Fractions then convert them to likeIf there are Unlike Fractions then convert them to like
fractions.fractions.
 The Denominator should not be subtracted.The Denominator should not be subtracted.
 Always change Improper fraction to a mixedAlways change Improper fraction to a mixed
fraction.fraction.
 The numerator can be negative.The numerator can be negative.

26. Subtracting FractionsSubtracting Fractions
Subtraction means taking objects away.
The objects must be of the same type, i.e. we
can only take away apples from a group of
apples.
In fractions, we can only take away pieces of
the same size.
In other words, the denominators must be
the same.

27. Subtracting Fractions WithSubtracting Fractions With
Same DenominatorsSame Denominators
- =
Subtract the numerator
and
leave the denominator as it is.
4 2 2 14 2 2 1
= == =
6 6 6 36 6 6 3

28. Subtracting Fractions withSubtracting Fractions with
Different DenominatorsDifferent Denominators
If there are different denominators in theIf there are different denominators in the
fractions, then we change them to likefractions, then we change them to like
fractions.fractions.
15
10
3
2
= =
5
2
15
65
2
3
2
−
15
4
15
6
15
10
5
2
3
2
=−=−

29. Subtracting Mixed FractionsSubtracting Mixed Fractions
Change the Mixed fractions toChange the Mixed fractions to
Improper Fractions and then toImproper Fractions and then to
Like Fractions.Like Fractions.
At last subtract the ImproperAt last subtract the Improper
Like Fractions.Like Fractions.
Don’t forget to change theDon’t forget to change the
answer to Mixed Fraction again.answer to Mixed Fraction again.

30. Multiplication Of FractionsMultiplication Of Fractions
Things To Know !!!!Things To Know !!!!
 SimplifyingSimplifying
 The Denominator are always multiplied.The Denominator are always multiplied.
 ““ Of ” : Of means multiply. E.g. : ½ of 2 = ½Of ” : Of means multiply. E.g. : ½ of 2 = ½ × 2 = 1× 2 = 1
 Product of two Proper Fractions is always less than both of them.Product of two Proper Fractions is always less than both of them.
 Product of two Improper Fractions is alwaysProduct of two Improper Fractions is always greatergreater than both ofthan both of
them.them.
 Product of one Improper Fraction and one ProperProduct of one Improper Fraction and one Proper
Fraction is always less than the Improper FractionFraction is always less than the Improper Fraction
and greater than the Proper Fraction.and greater than the Proper Fraction.

31. Multiplying FractionsMultiplying Fractions
To Multiply Fractions we Multiply both - TheTo Multiply Fractions we Multiply both - The
numerators and the Denominators separately.numerators and the Denominators separately.
2 3 22 3 2 ×× 3 6 33 6 3
×× = == = ==
4 2 4 × 2 8 44 2 4 × 2 8 4

32. Multiplying Mixed FractionsMultiplying Mixed Fractions
Change the Mixed fractions toChange the Mixed fractions to
Improper Fractions.Improper Fractions.
Then multiply the ImproperThen multiply the Improper
Fraction.Fraction.
Don’t forget to change theDon’t forget to change the
answer to Mixed Fraction again.answer to Mixed Fraction again.

33. Addition Of FractionsAddition Of Fractions
Things To Know !!!!Things To Know !!!!
 SimplifyingSimplifying
 MultiplicationMultiplication
 Always change Improper fraction to a mixed fraction.Always change Improper fraction to a mixed fraction.
 Reciprocal: The inverse of fractionReciprocal: The inverse of fraction
E.g. – 2/3 = 3/2 = 1 ½ , 2 ½ = 5/2 = 2/5E.g. – 2/3 = 3/2 = 1 ½ , 2 ½ = 5/2 = 2/5

34. Dividing FractionsDividing Fractions
To Divide Fractions we change the Second Fraction
with its Reciprocal.
Then Multiply the Reciprocal with the First
Fraction.
2 4 2 × 5 10 5
÷ = = =
4 5 4 × 4 16 8

35. Dividing Mixed FractionsDividing Mixed Fractions
Change the Mixed fractions toChange the Mixed fractions to
Improper Fractions.Improper Fractions.
Then Multiply the ImproperThen Multiply the Improper
Fraction.Fraction.
Don’t forget to change theDon’t forget to change the
answer to Mixed Fraction again.answer to Mixed Fraction again.

36. ComparisonComparison
ComparisonComparison
• Greater than and Smaller thanGreater than and Smaller than
• How does the Denominator controls the FractionHow does the Denominator controls the Fraction
• How does the Numerator controls the FractionHow does the Numerator controls the Fraction

37. Greater than and Smaller thanGreater than and Smaller than
Change the Fractions to Like Fractions.
The fraction with greater numerator is bigger
than the other one.
If the Numerators are same, then the Fraction
with smallest Denominator is the Biggest.
>
2 3 10 9
& =
3 5 15 15

38. How does the DenominatorHow does the Denominator
controls the Fractioncontrols the Fraction
Denominator represents the total number of pieces.Denominator represents the total number of pieces.
If we share a Pizza with 2 people, we get ½ of pizza.If we share a Pizza with 2 people, we get ½ of pizza.
If we share a Pizza with 4 people, we get ¼ of pizza.If we share a Pizza with 4 people, we get ¼ of pizza.
If we share a Pizza with 8 people, we get 1/8 of pizza.If we share a Pizza with 8 people, we get 1/8 of pizza.
Conclusion:Conclusion:
The larger the denominator the smaller the pieces, andThe larger the denominator the smaller the pieces, and
if the numerator is kept fixed, the larger theif the numerator is kept fixed, the larger the
denominator the smaller the fraction,denominator the smaller the fraction,

39. How does the Numerator controlsHow does the Numerator controls
the Fractionthe Fraction
Numerator represents the number of pieces.Numerator represents the number of pieces.
If we share a Pizza with 16 people, we get 1/16 of pizza.If we share a Pizza with 16 people, we get 1/16 of pizza.
If we share a Pizza with 13 people, we get 3/16 of pizza.If we share a Pizza with 13 people, we get 3/16 of pizza.
If we share a Pizza with 5 people, we get 5/16 of pizza.If we share a Pizza with 5 people, we get 5/16 of pizza.
Conclusion :Conclusion :
When the numerator gets larger we have more pieces.When the numerator gets larger we have more pieces.
And if the denominator is kept fixed, the larger numeratorAnd if the denominator is kept fixed, the larger numerator
makes a bigger fraction.makes a bigger fraction.