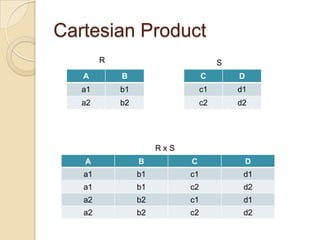
The document discusses three relational algebra operations: rename, cartesian product, and selection with a join. The rename operation changes the name of a relation without altering the tuples. The cartesian product pairs all tuples of one relation with all tuples of another relation, resulting in a cross join. The example operation selects tuples from two joined relations where the high school is over 1000 and the major is computer science with a rejection decision.

2. The rename operation
 It is denoted as ρ
 E : relational algebra expression
 ρ x (E): returns the result of
expression E under the name x.
 ρ x (A1, A2, A3… An) (E): returns the
result of expression E under the name
x with attributes renamed to A1, A2,
A3… An.

3. Rename Operator
 The rename operator returns an existing relation
under a new name.
 ρA(B) is the relation B with its name changed to A.
Name EmployeeId
Harry 3415
Sally 2241
EmployeeName EmployeeId
Harry 3415
Sally 2241
Employee

4. Cartesian Product
 If R and S are two relations, R S is the set
of all concatenated tuples <x,y>, where x is
a tuple in R and y is a tuple in S
◦ R and S need not be union compatible.
◦ But R and S must have distinct attribute names.
 Each row of R is paired with each row of S.
 Result schema has one field per field of S
and R, with field names `inherited’ if
possible.

5. Cartesian Product
A B
a1 b1
a2 b2
C D
c1 d1
c2 d2
A B C D
a1 b1 c1 d1
a1 b1 c2 d2
a2 b2 c1 d1
a2 b2 c2 d2
R S
R x S

6. sID sName GPA HS sID sName major dec
Student Apply
Q : Names and GPAs of students with HS >1000 who
applied to CS and were rejected
π sName , GPA
( σ Student.sID = Apply.sID ^ HS > 1000 ^ Major =‘cs’ ^ dec = ‘R’
( Student x Apply ) )