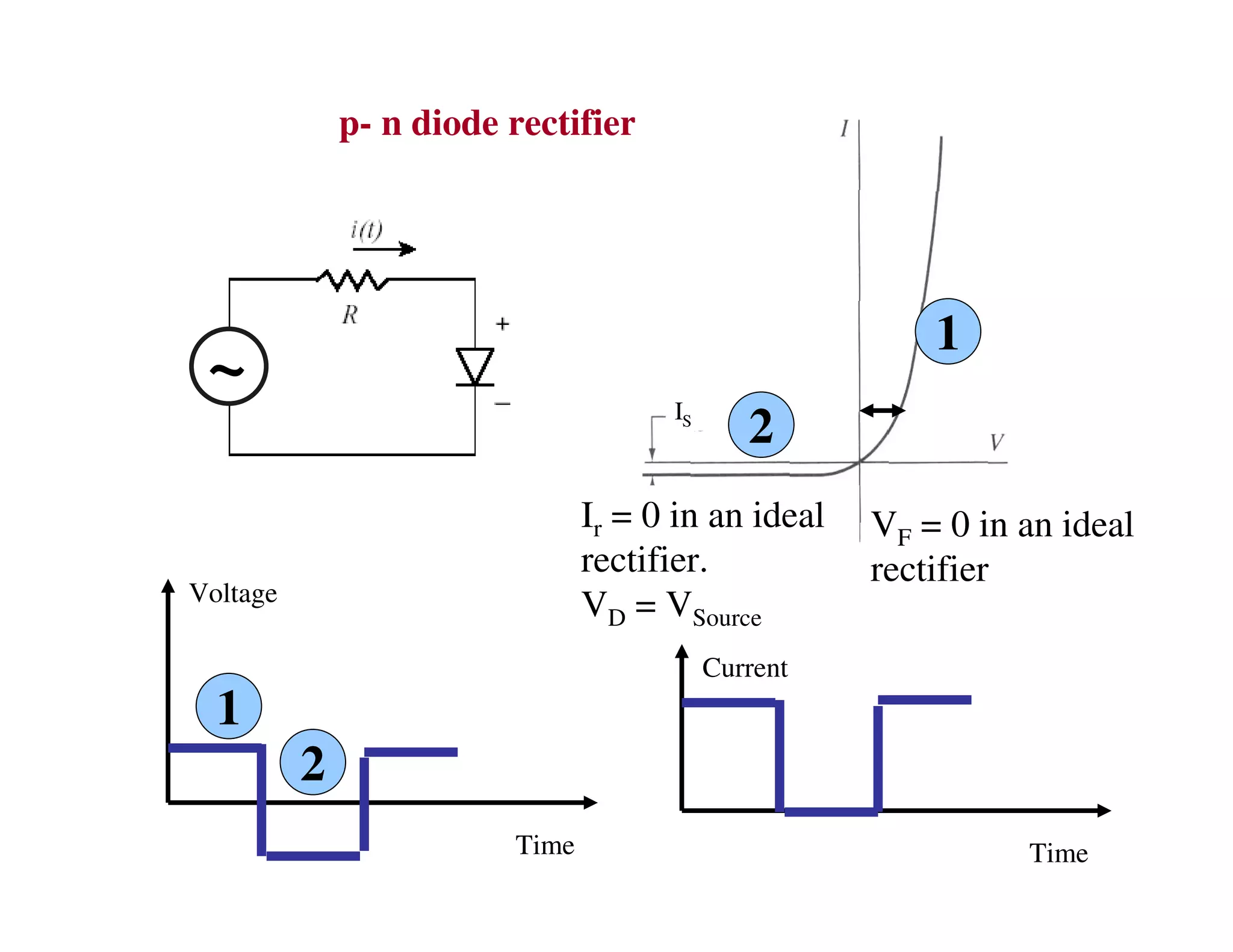
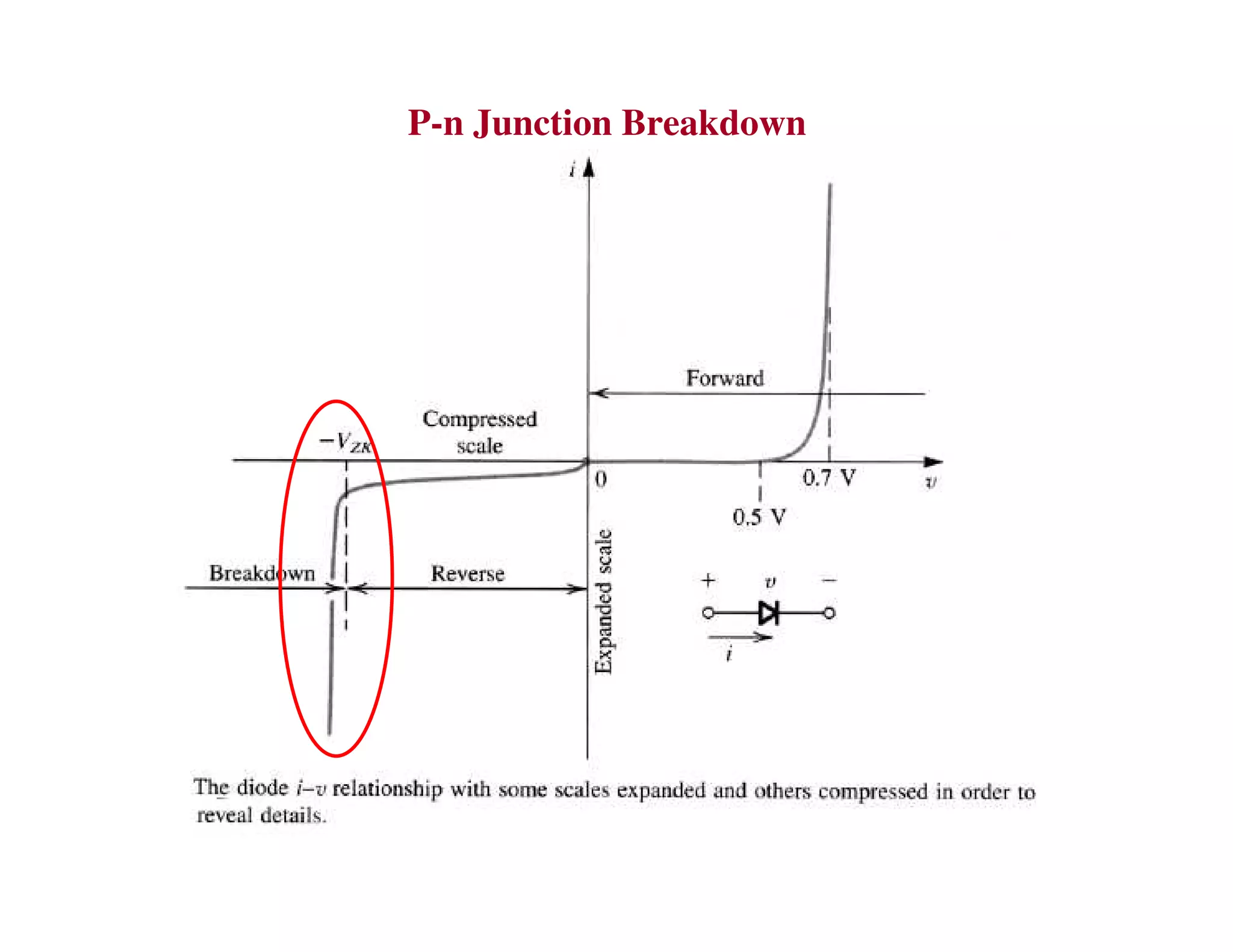
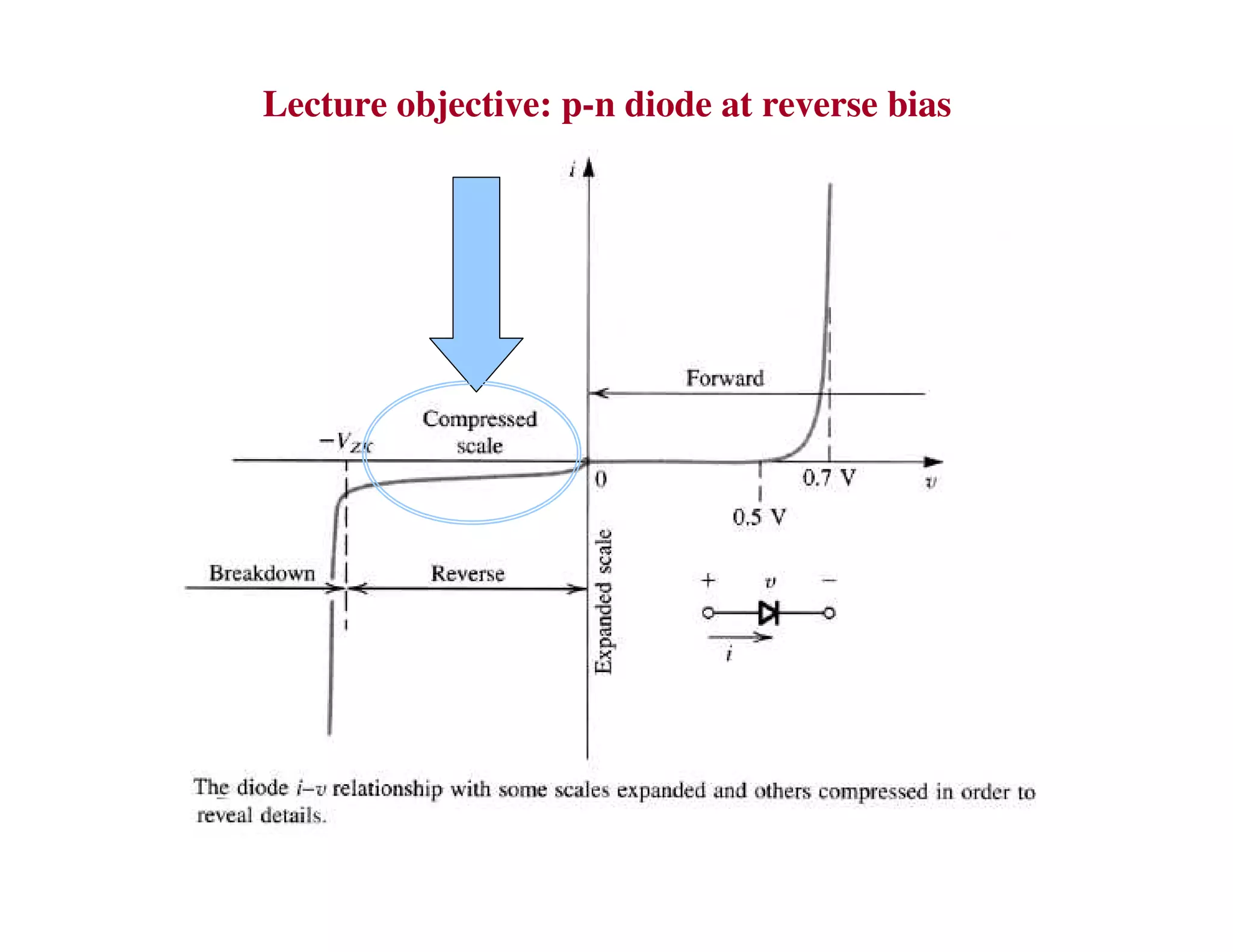
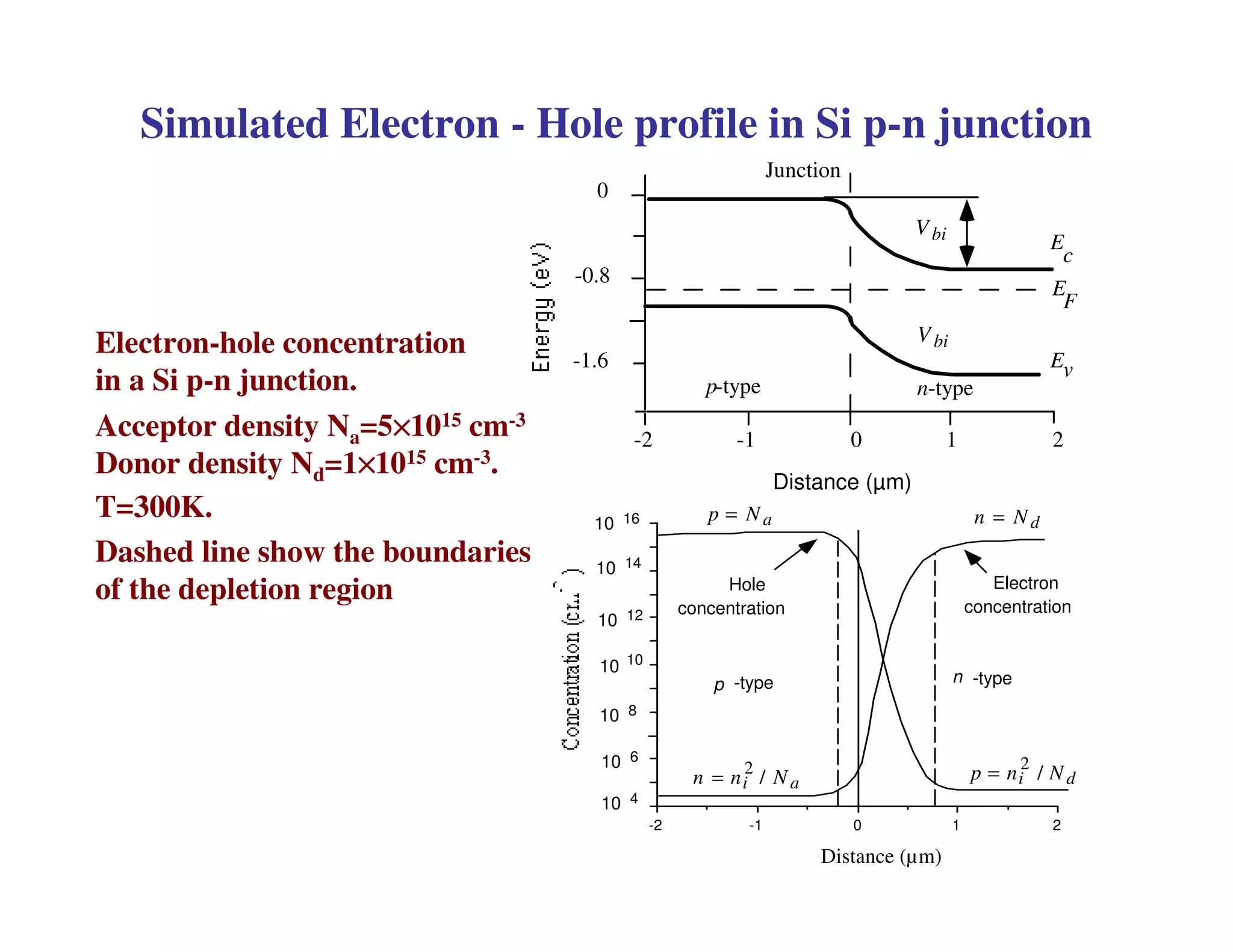
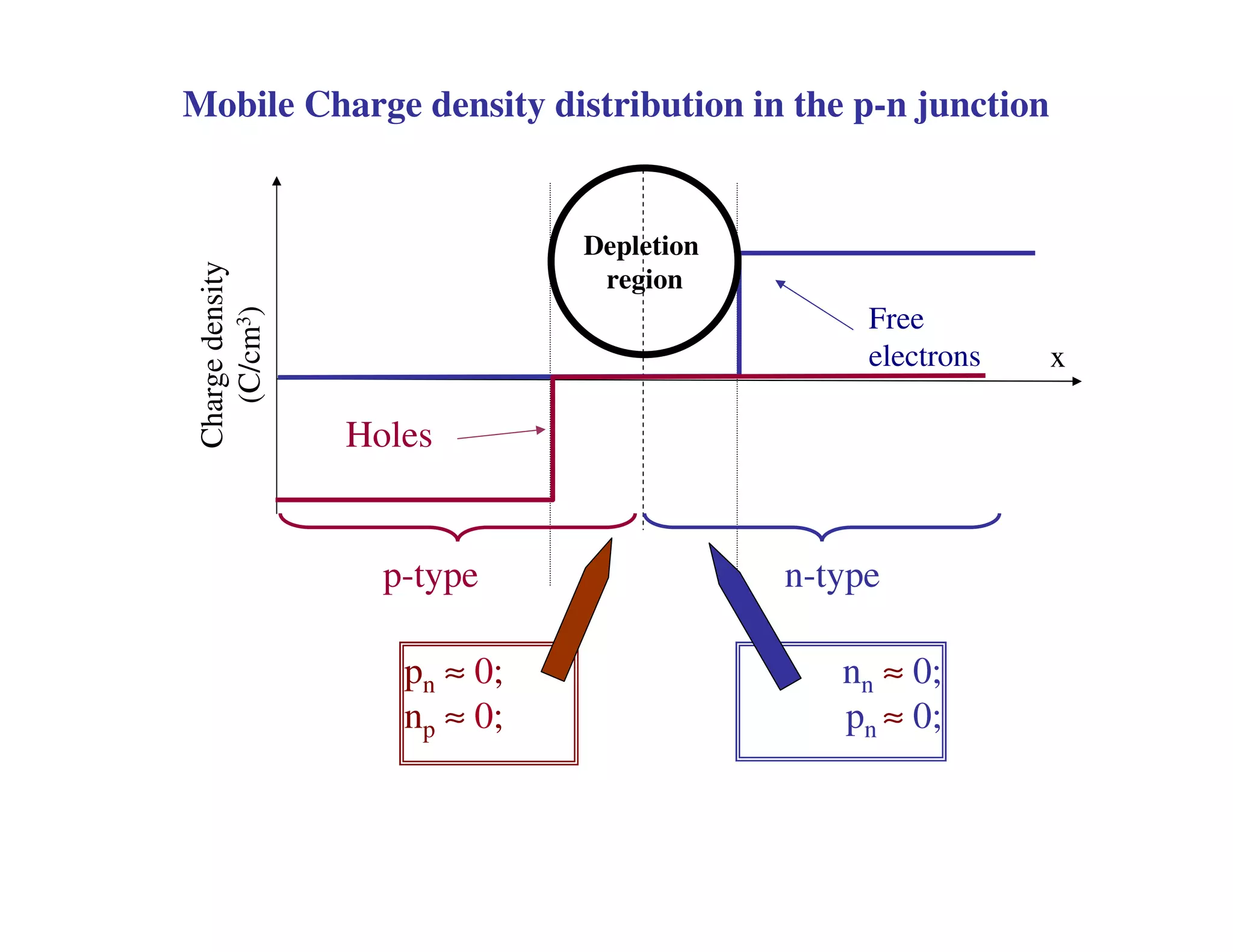
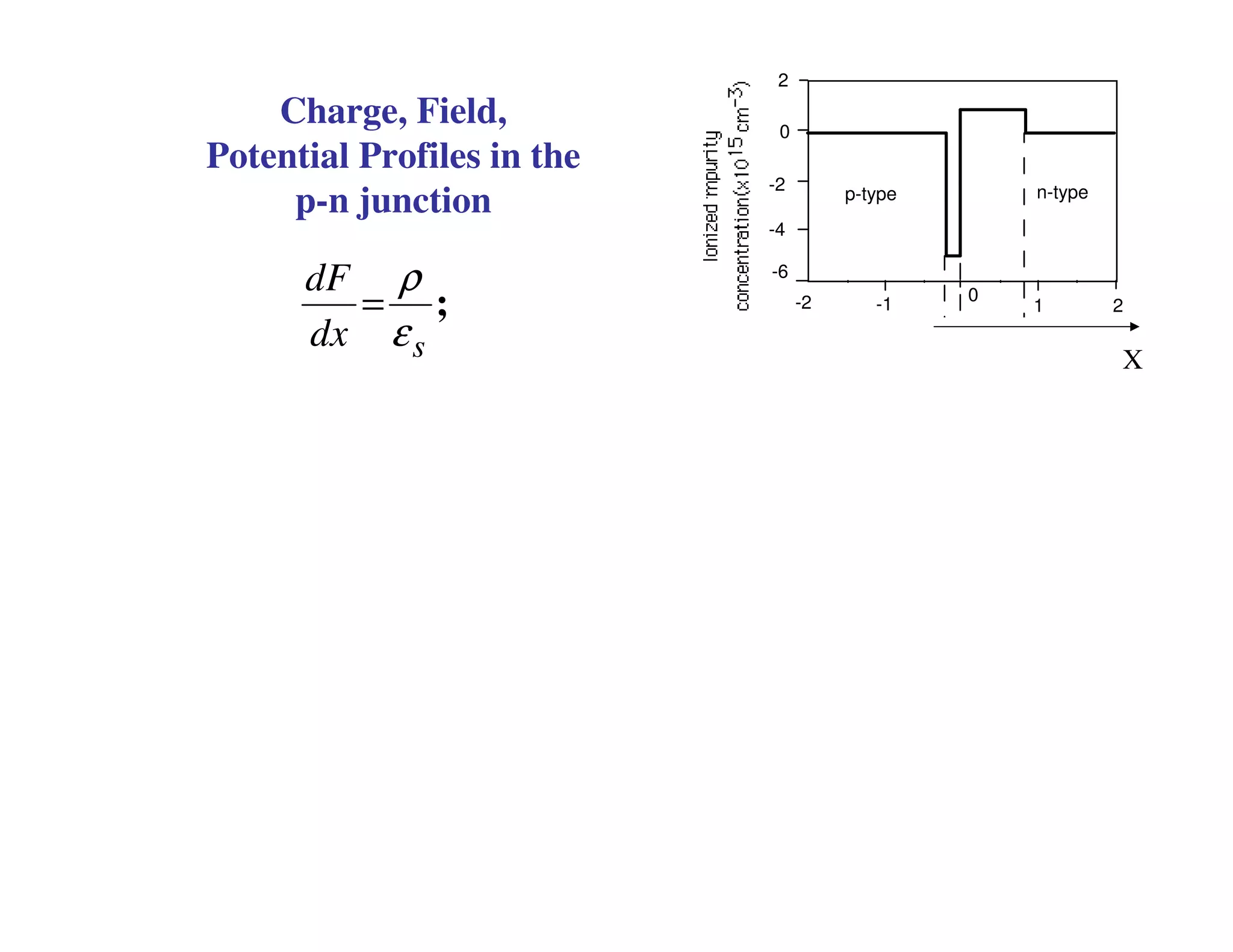
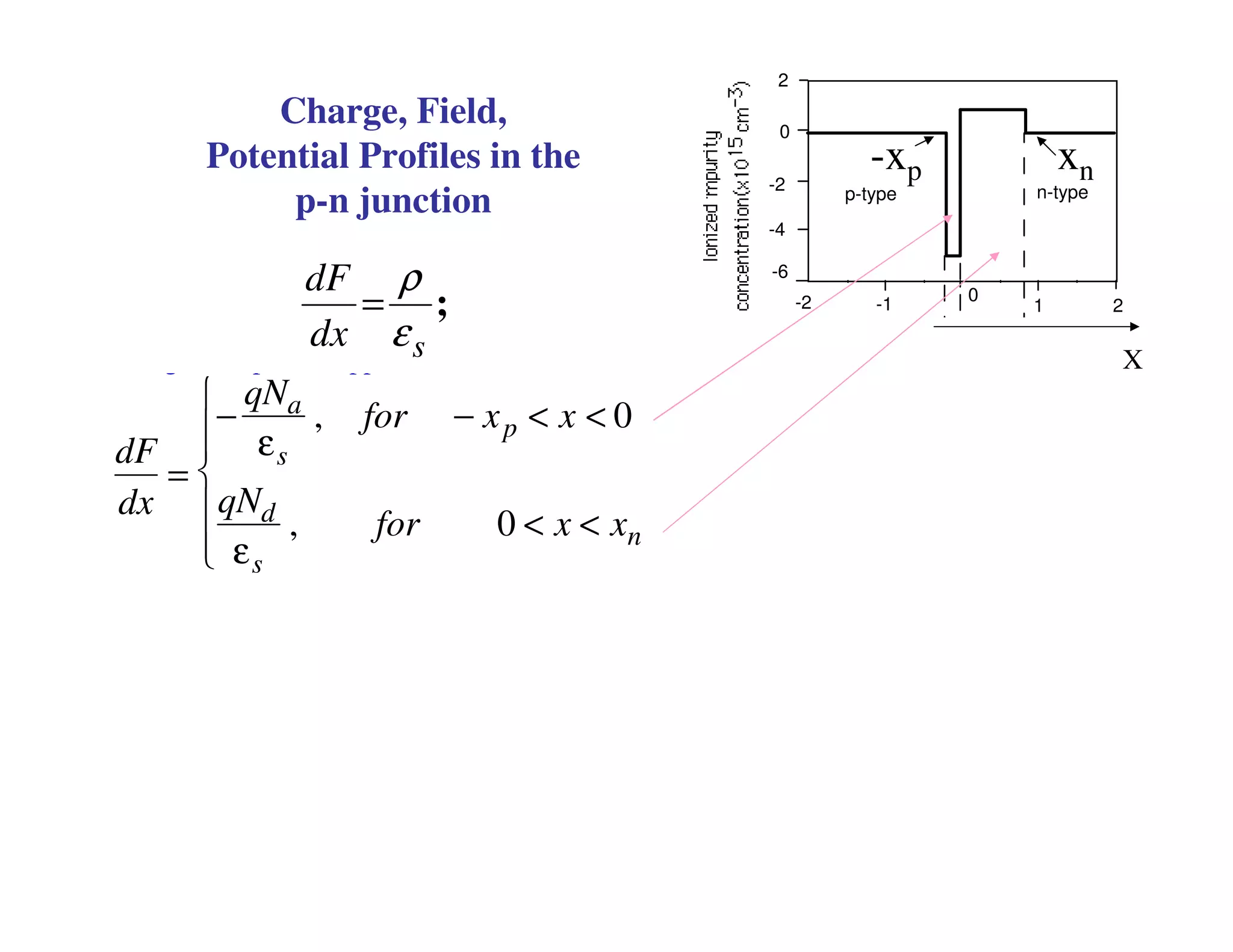
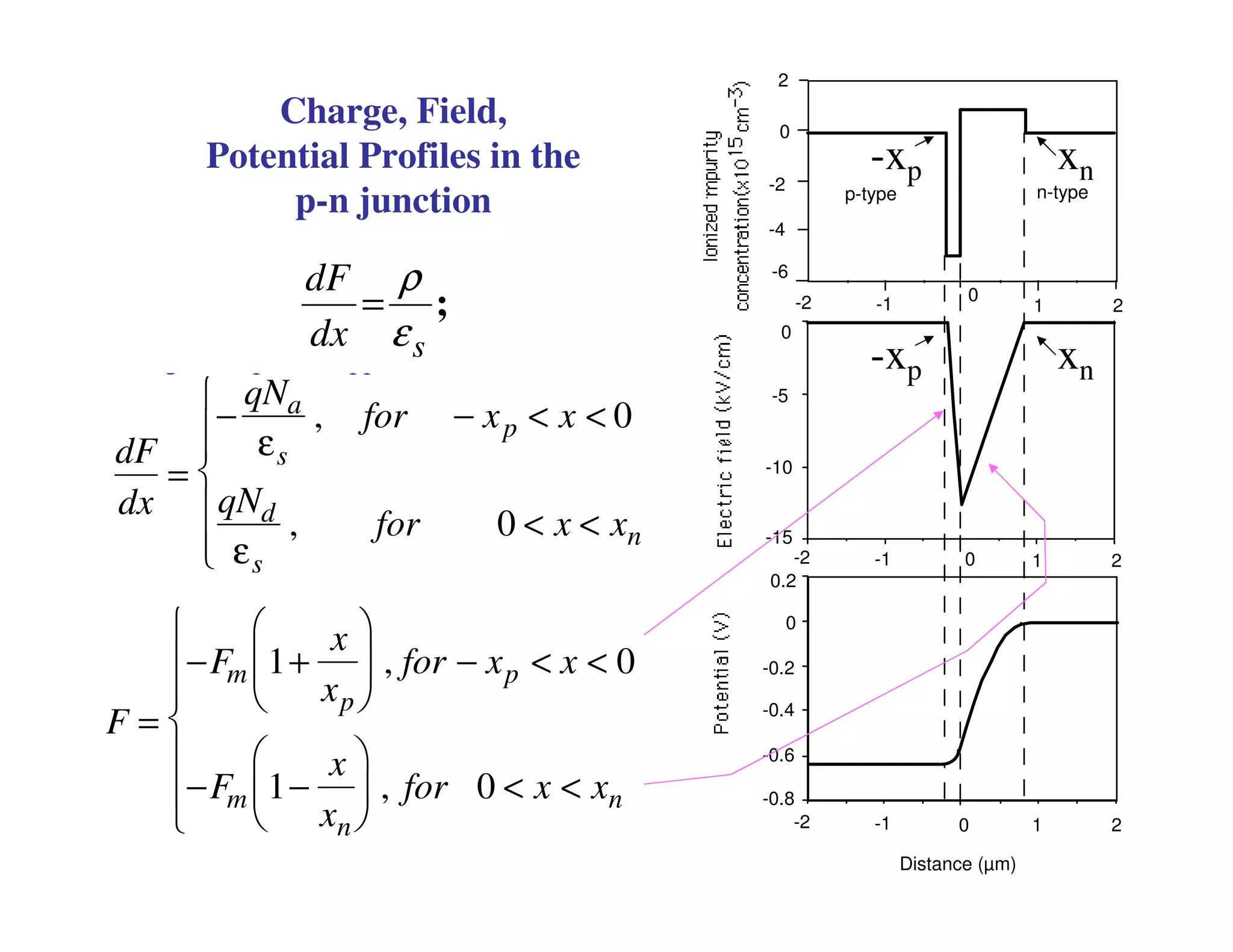
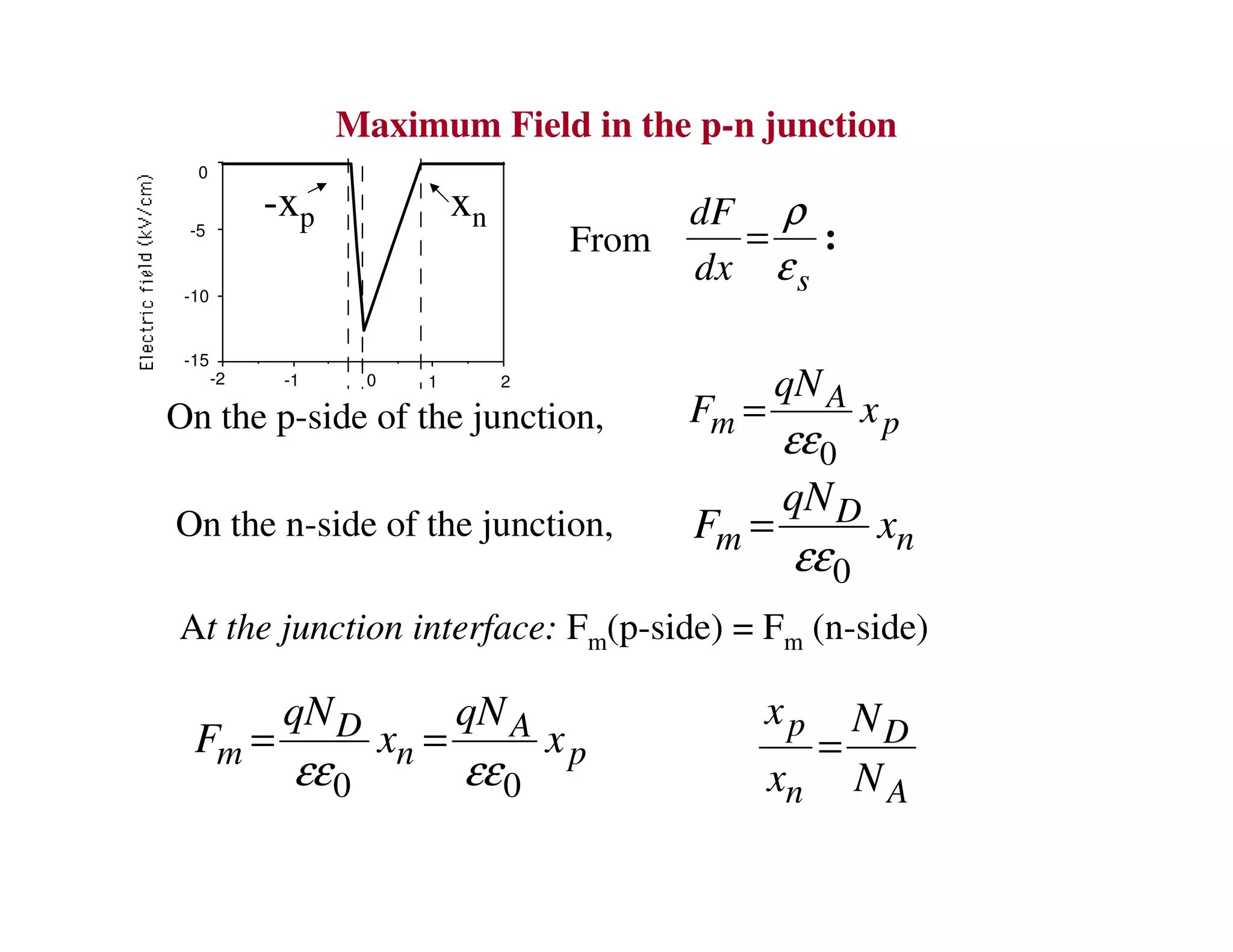
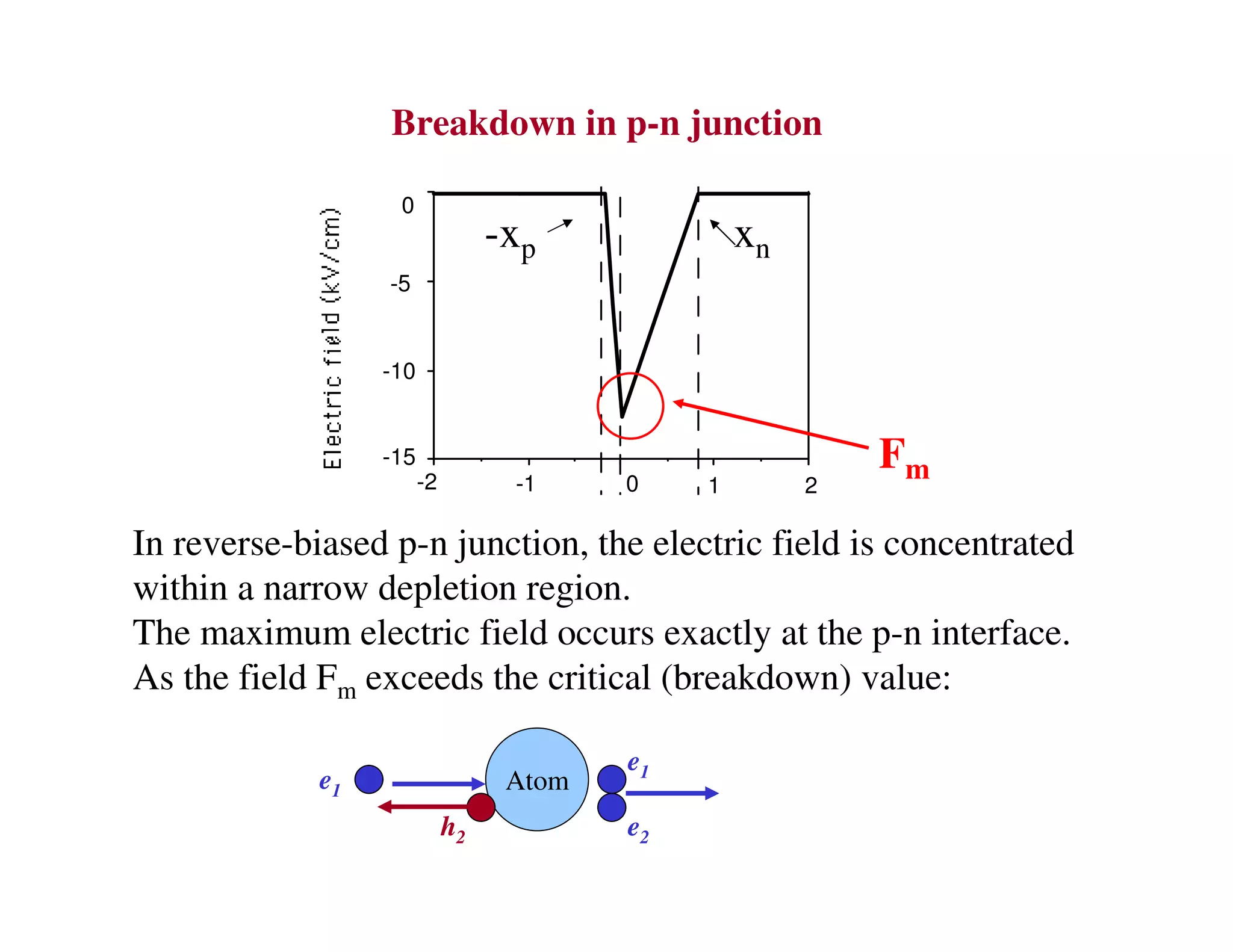
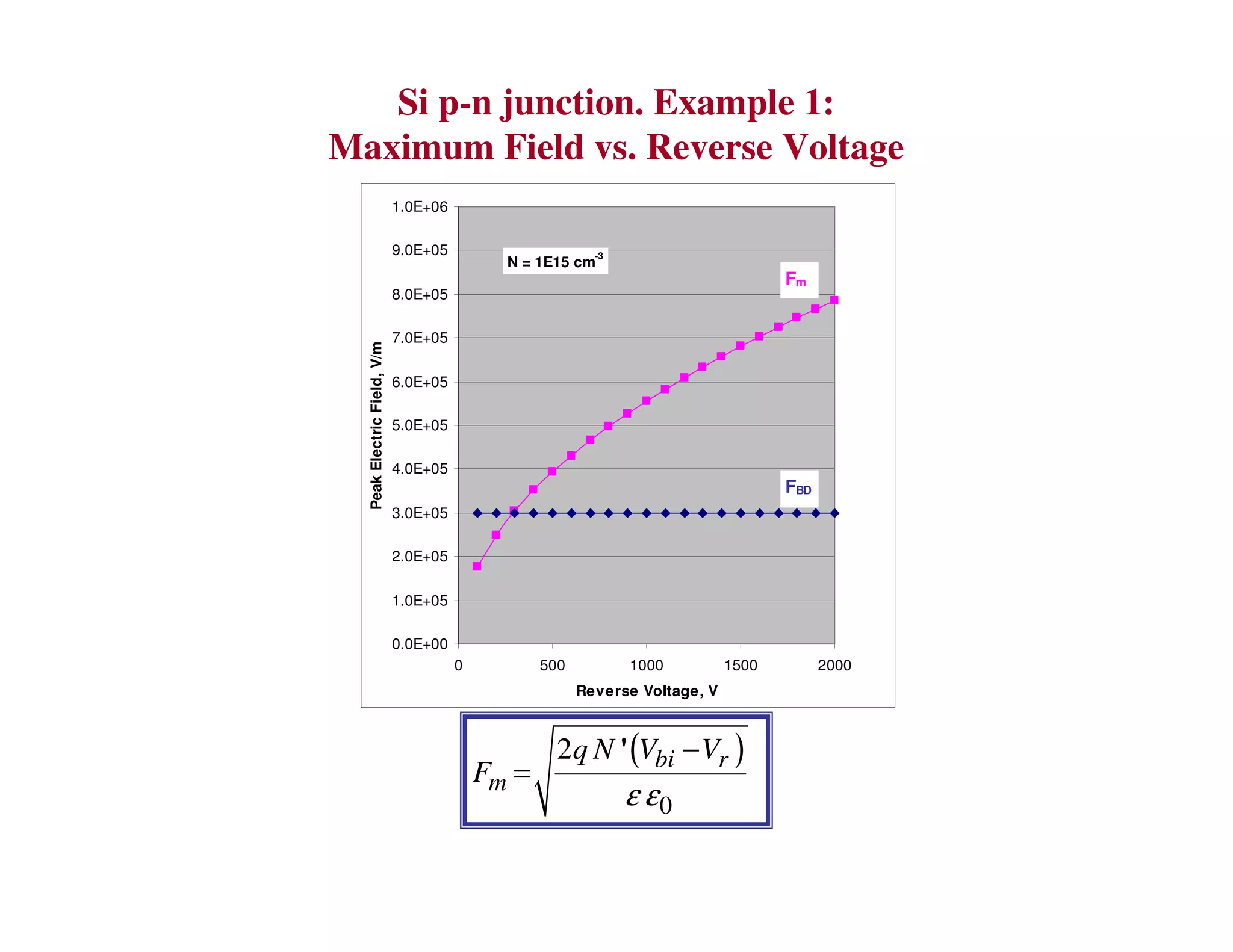
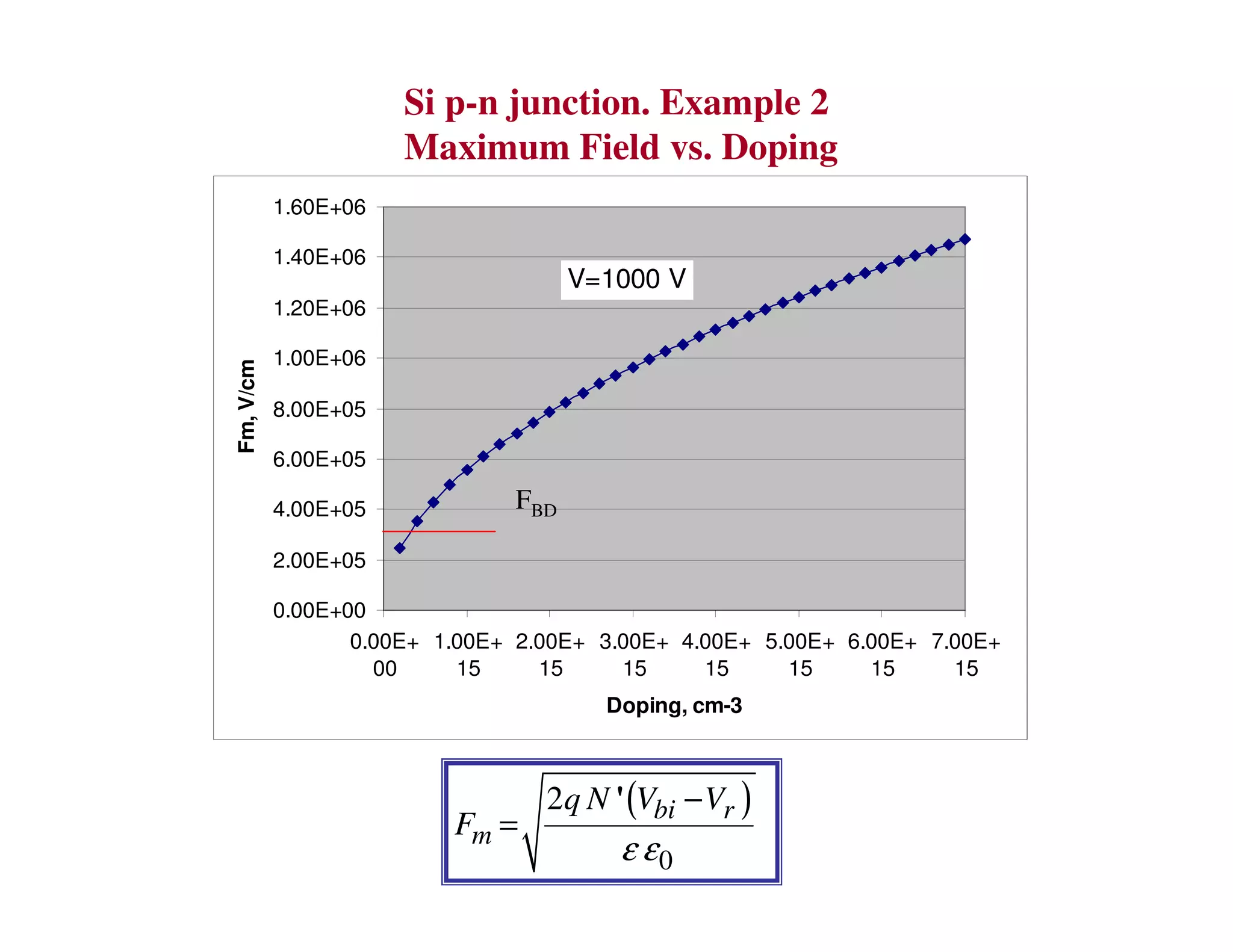
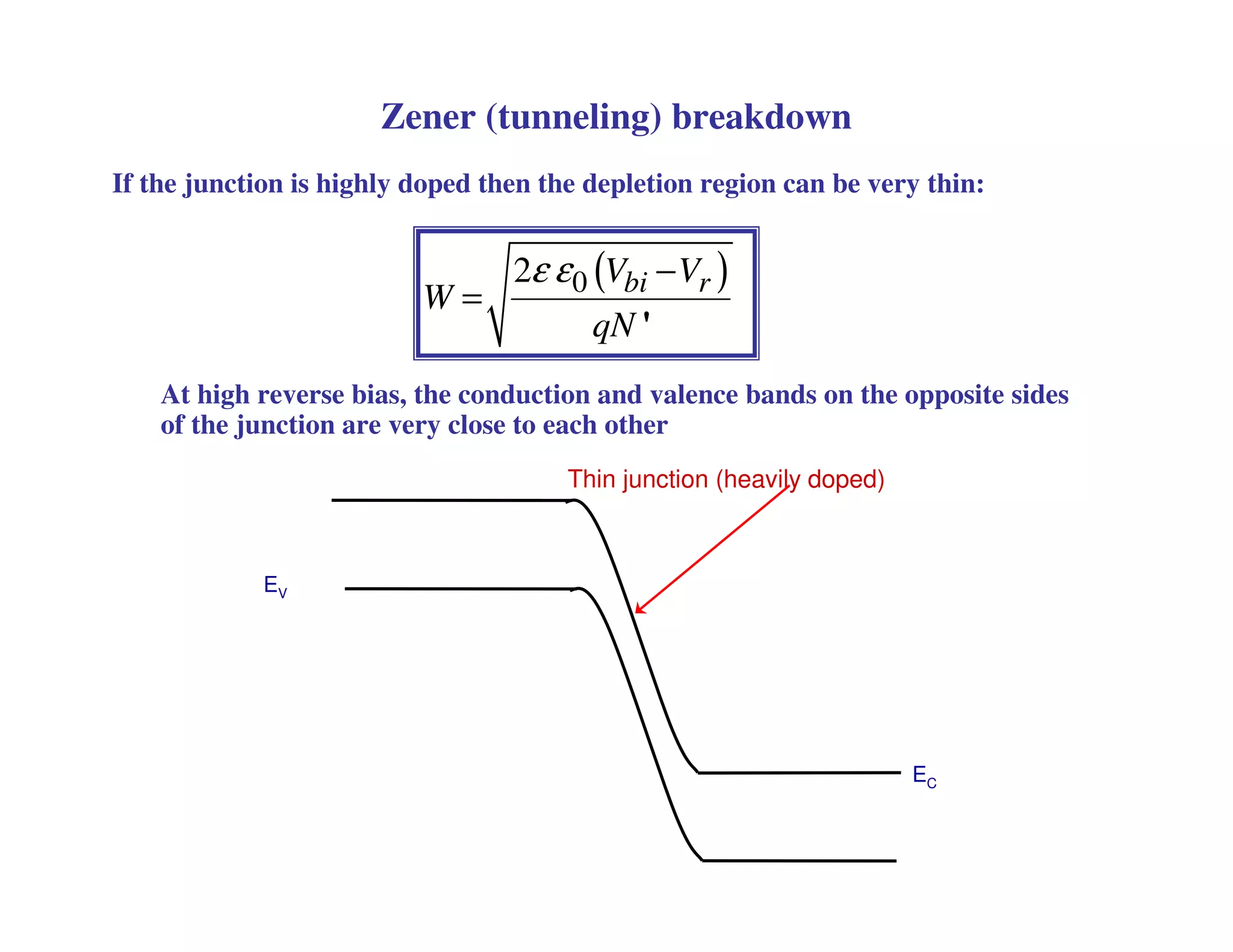
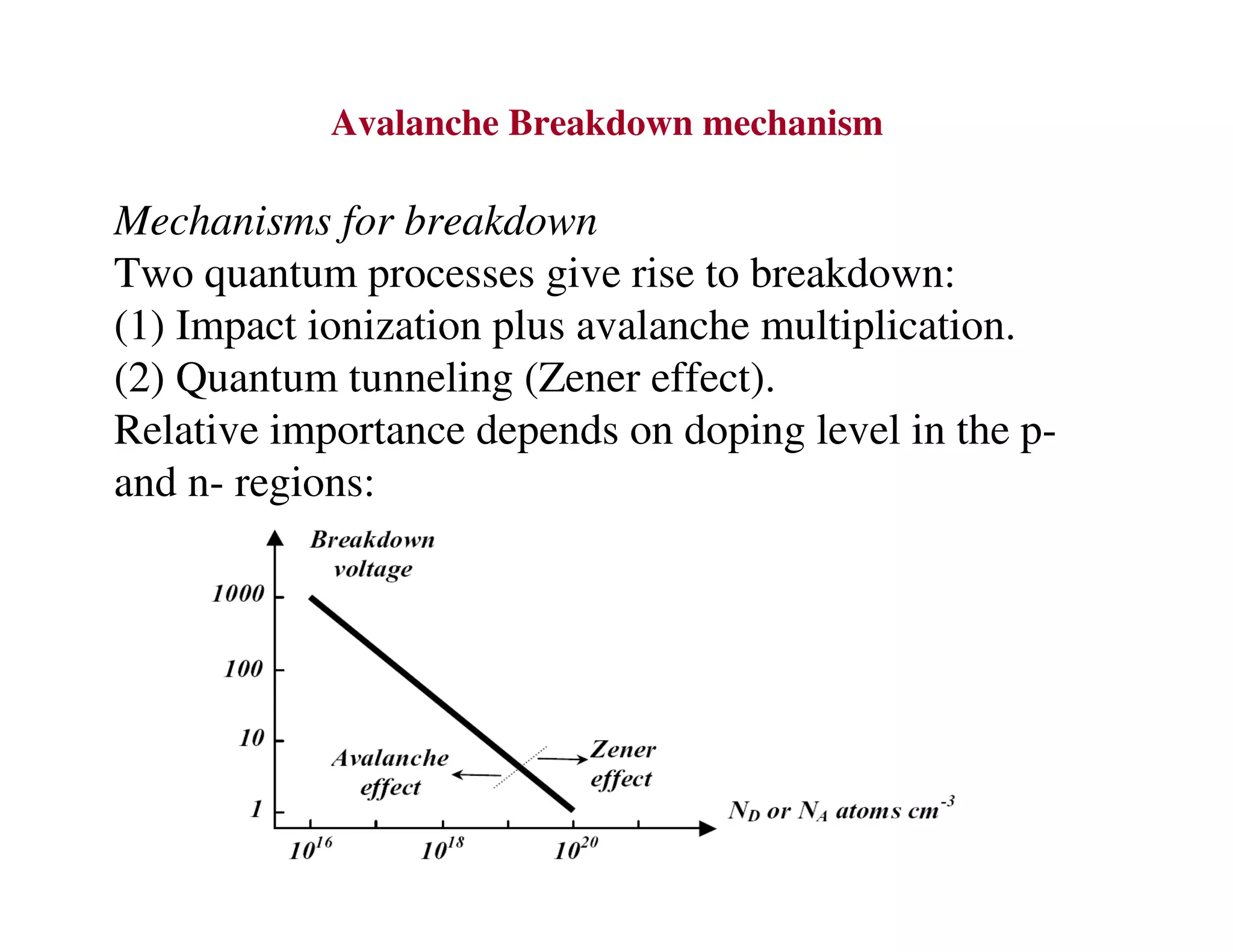
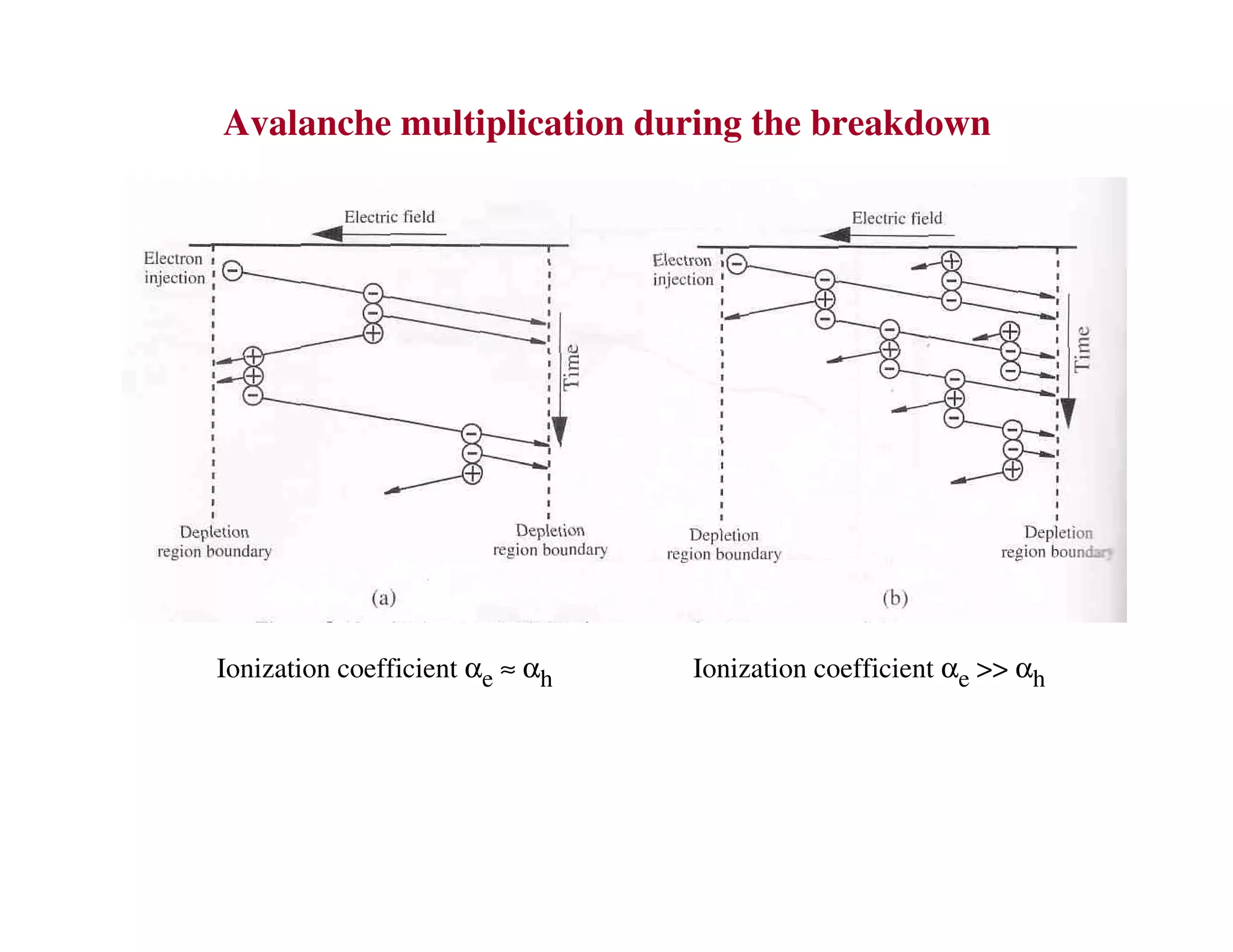
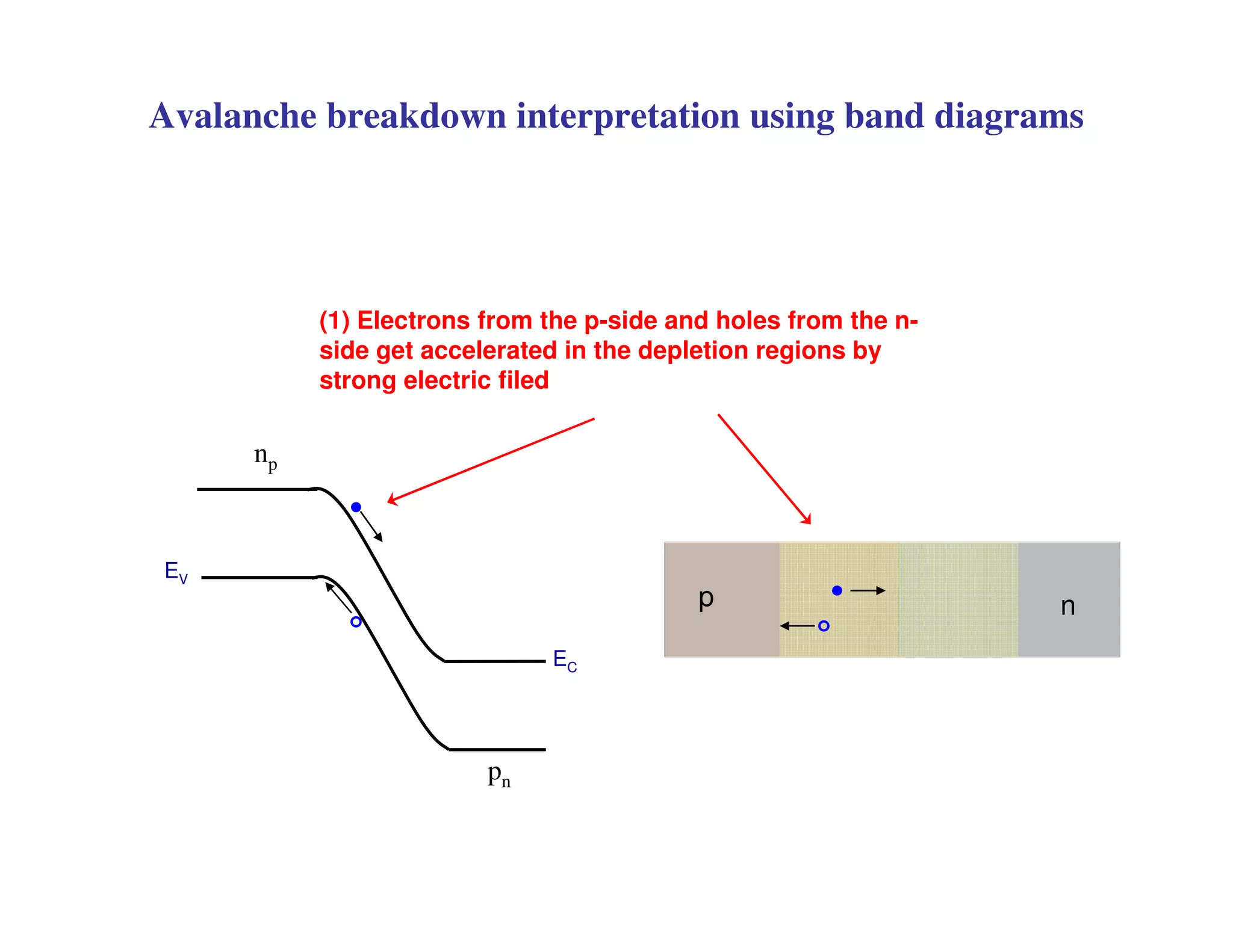
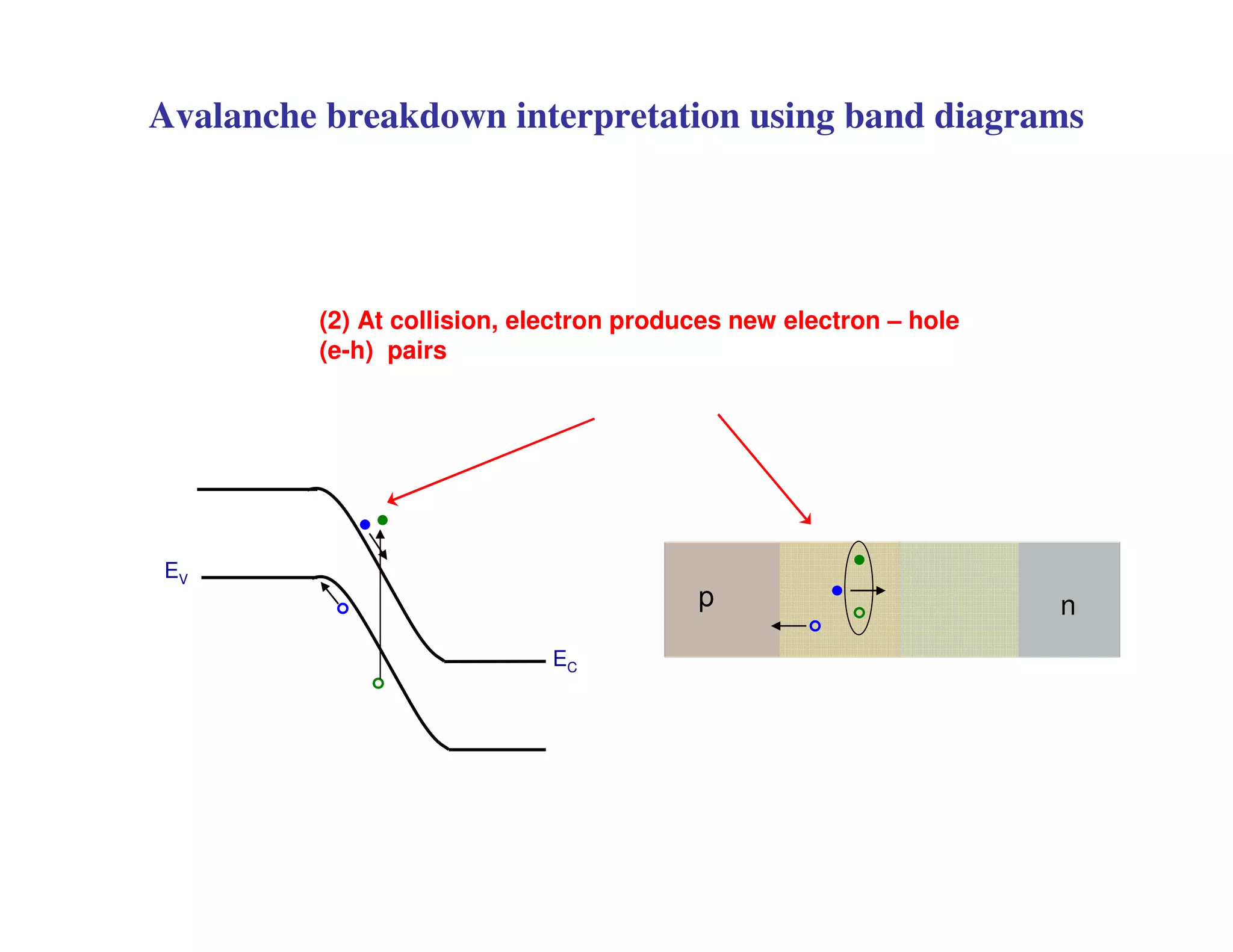
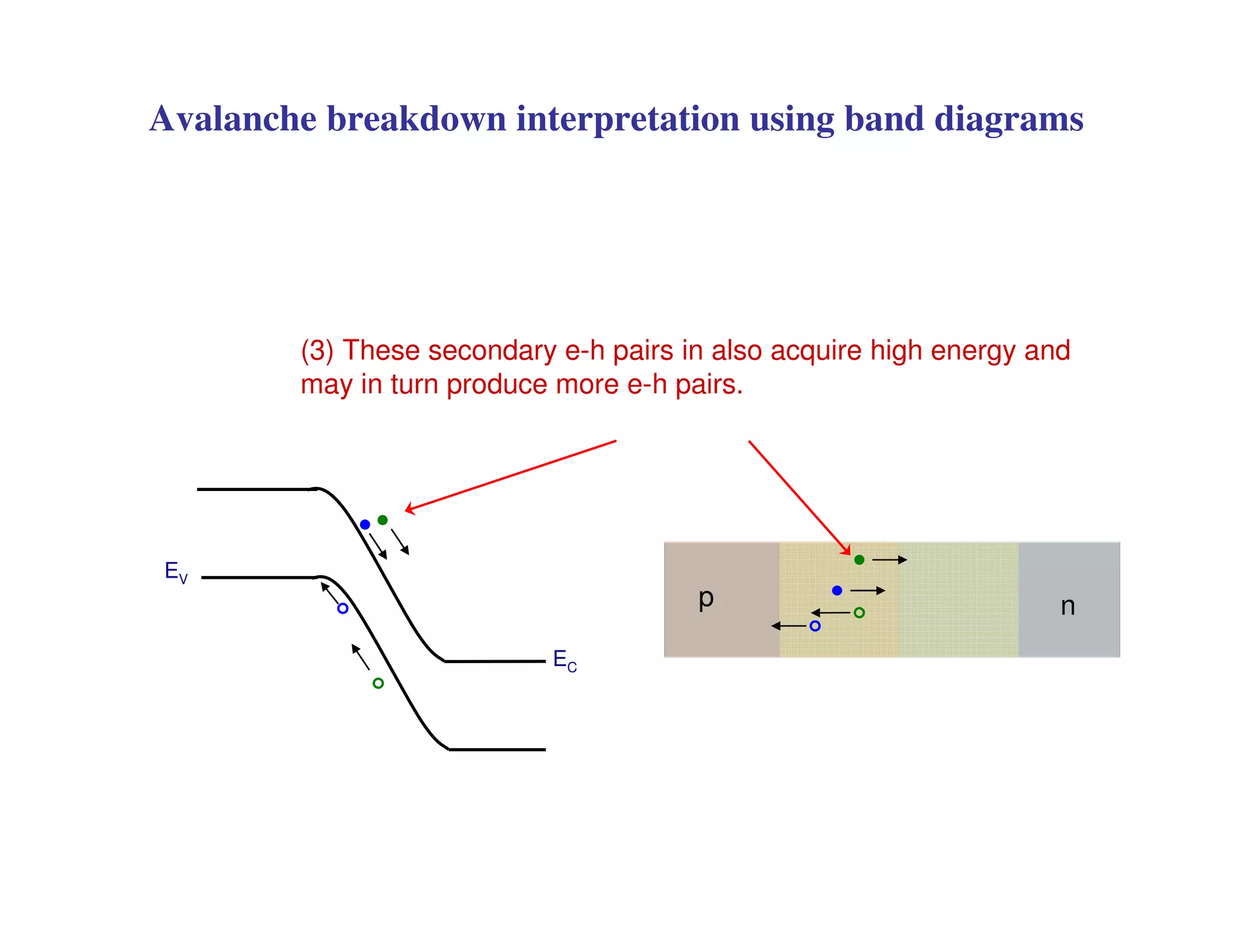
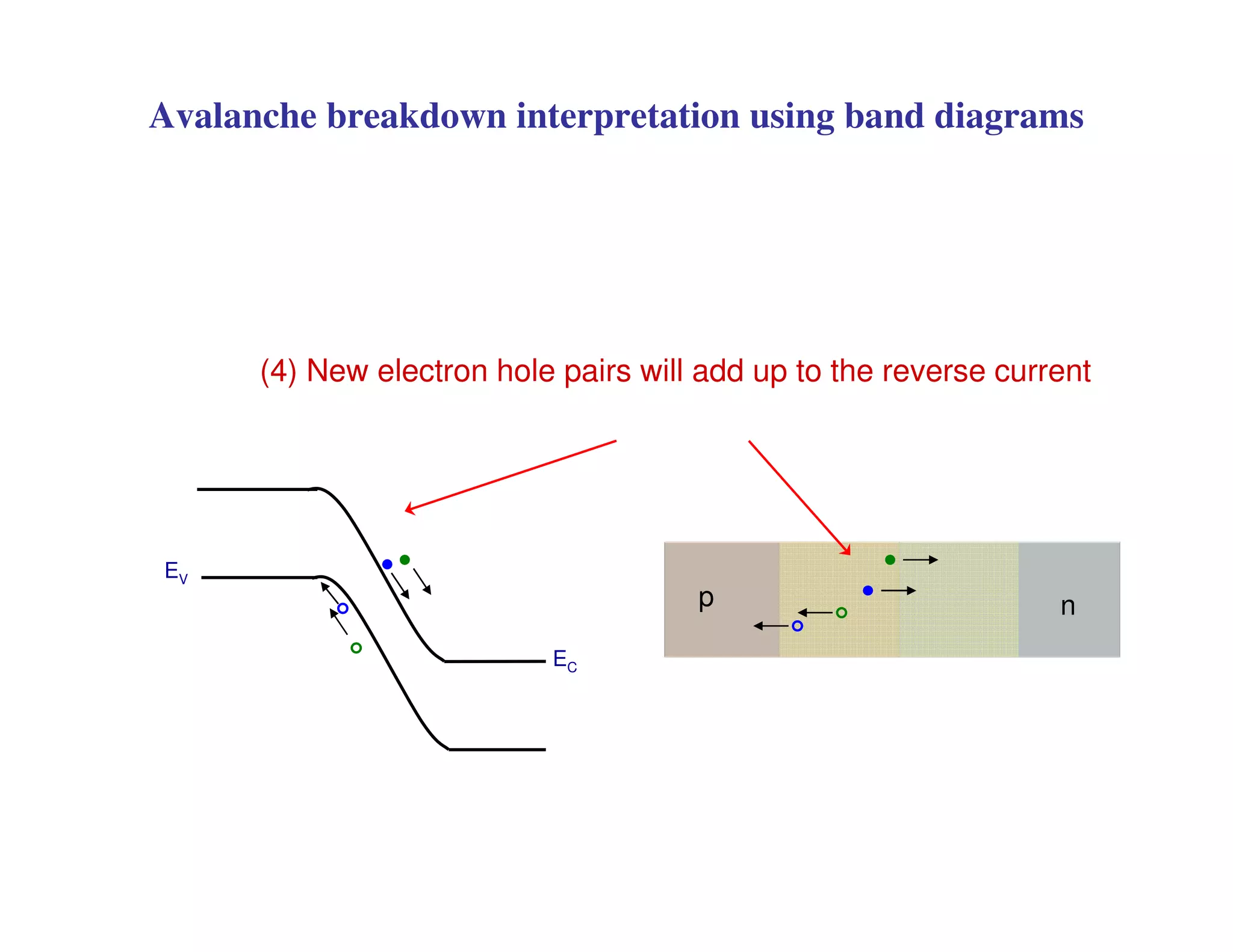
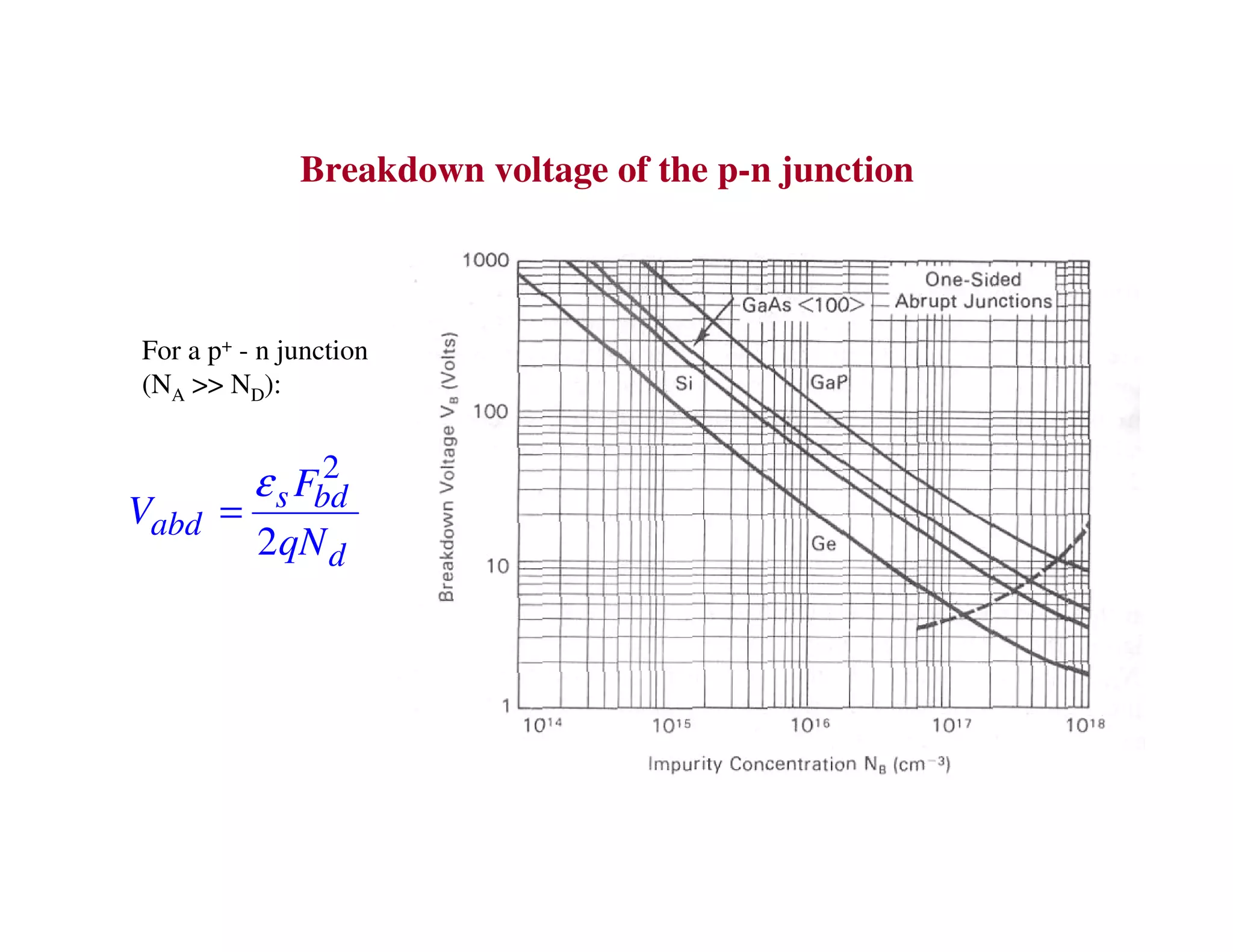
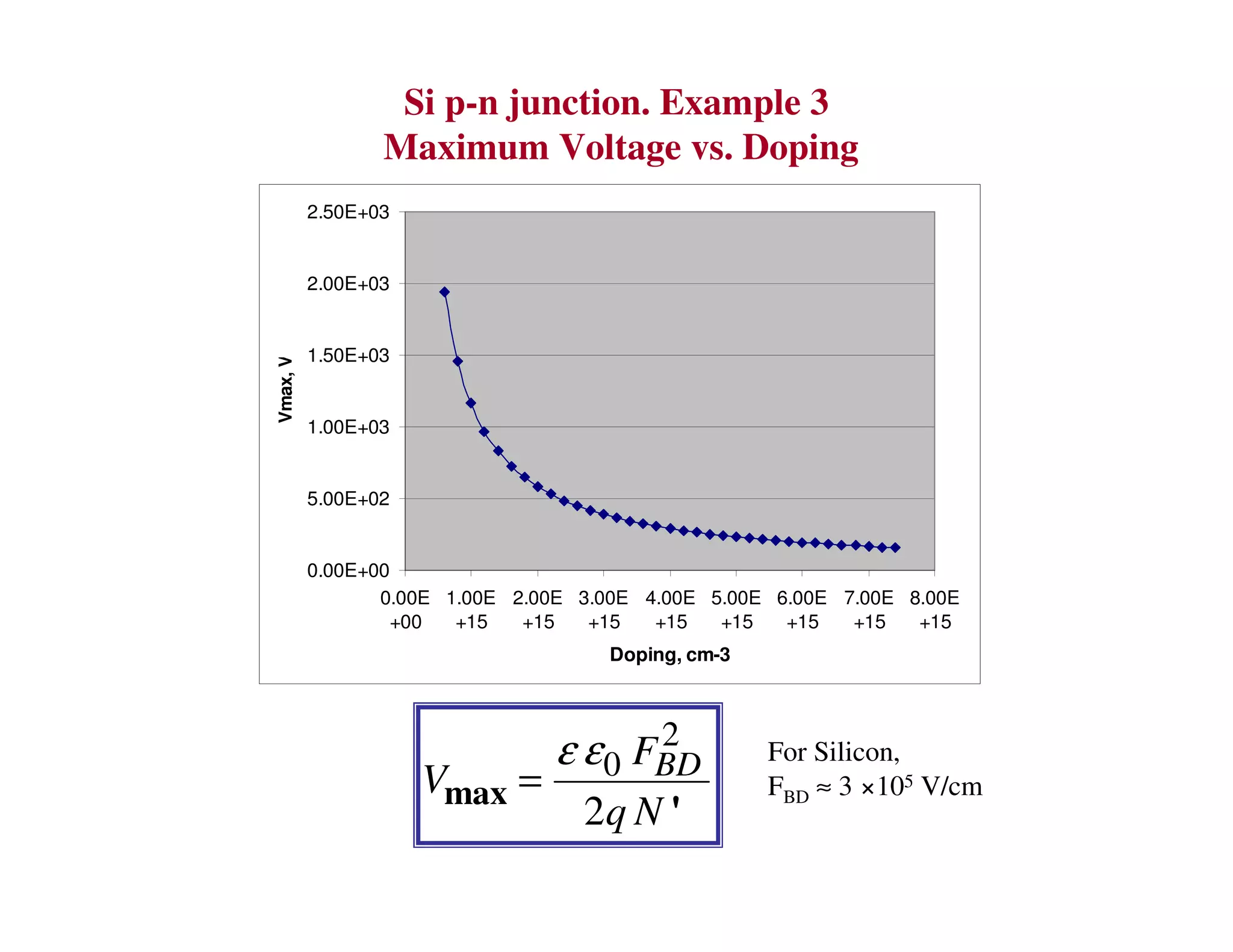
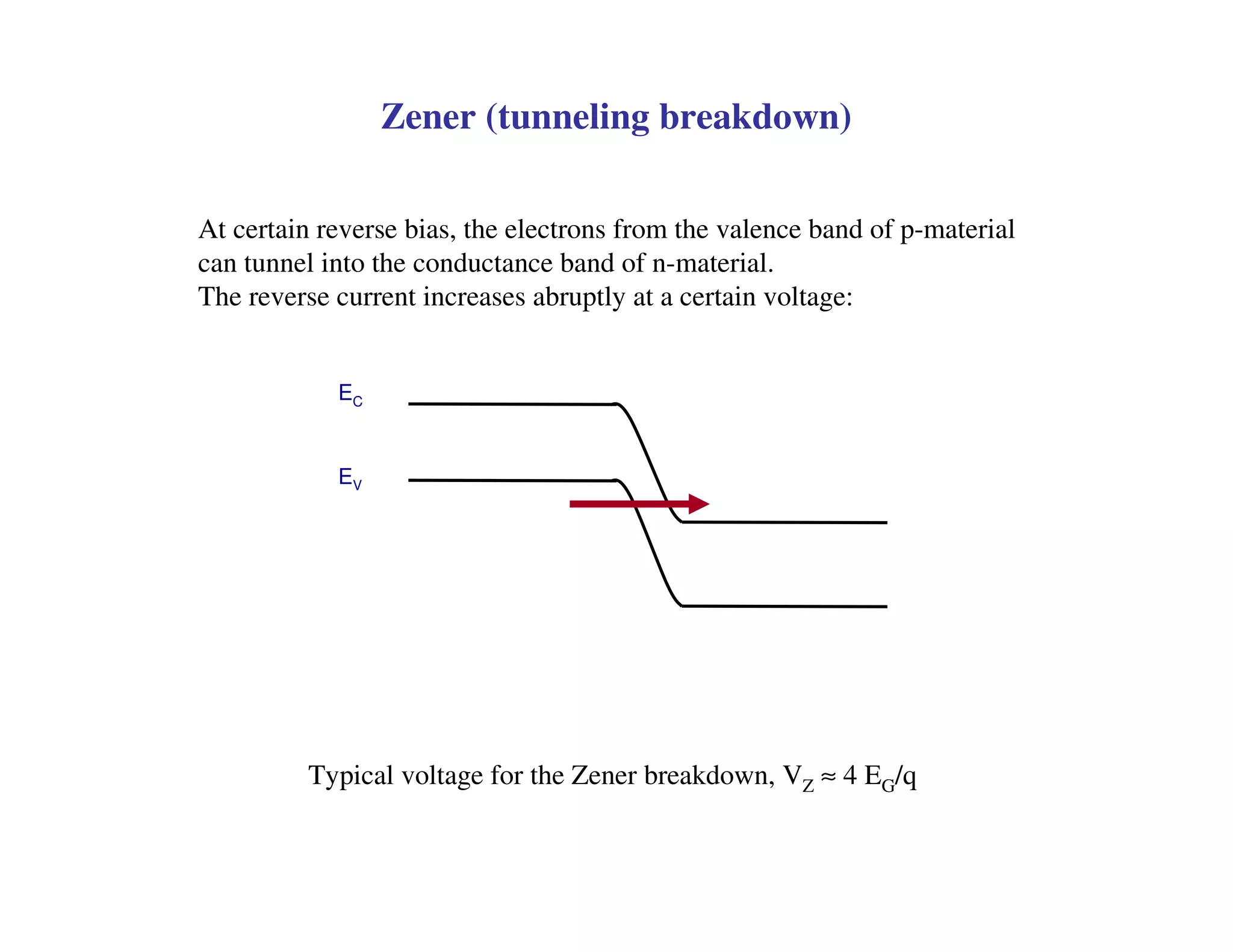
1. P-N diode rectifiers use the asymmetric conduction of P-N junctions to allow current in only one direction, rectifying an AC input into a pulsed DC output. 2. When a P-N junction is reverse biased, a depletion region forms where the P and N regions are depleted of mobile charge carriers. This results in a built-in electric field. 3. Under sufficient reverse bias, avalanche breakdown can occur where the built-in electric field accelerates carriers to energies high enough to liberate other carriers through impact ionization, causing an avalanche multiplication of carriers and a sharp rise in reverse current.

1. p- n diode rectifiers

2. p- n diode rectifiers






−1exp
kT
qV
IS






−1exp
kT
qV
IS
~
Time
Current
1
VF = 0 in an ideal
rectifier
Time
Voltage
1
2
2
Ir = 0 in an ideal
rectifier.
VD = VSource

3. Lecture objective: p-n diode at reverse bias

4. Simulated Electron - Hole profile in Si p-n junction
Electron-hole concentration
in a Si p-n junction.
Acceptor density Na=5××××1015 cm-3
Donor density Nd=1××××1015 cm-3.
T=300K.
Dashed line show the boundaries
of the depletion region
Vbi
Junction
-2 -1 0 1 2
Distance (µm)
0
-0.8
-1.6
E
F
E
c
Ev
p-type n-type
Vbi
210-1-2
10 16
10 14
10 12
10 10
10 8
10 6
10 4
Distance (µm)
p -type n -type
Electron
concentration
Hole
concentration
p = Na n = Nd
n = ni
2
/ Na
p = ni
2
/ Nd

5. pn ≈ 0;
np ≈ 0;
ρ ≈ -q NA;
nn ≈ 0;
pn ≈ 0;
ρ ≈ +q ND;
Concentration
x
ND
np
NA
ρ = 0; ρ = 0;
Charge distribution in the depletion region.
Total charge density in the semiconductor: ρρρρ = q××××(Nd + p - Na - n);

6. pn ≈ 0;
np ≈ 0;
nn ≈ 0;
pn ≈ 0;
Chargedensity
(C/cm3)
x
Free
electrons
Holes
Mobile Charge density distribution in the p-n junction
Depletion
region
p-type n-type

7. pn ≈ 0;
np ≈ 0;
ρ ≈ -q NA;
nn ≈ 0;
pn ≈ 0;
ρ ≈ +q ND;
Chargedensity
(C/cm3)
x
qND
qNA
ρ = 0; ρ = 0;
Charge distribution in the depletion region.
Total charge density in the semiconductor: ρρρρ = q××××(Nd + p - Na - n);

8. In the following material, the electric field is
denoted as “F”
(to distinguish from “E” = electron/hole energy).
0
0
s
s
dF
dx
where isthecharge density
ρ ρ
ε ε ε
ε ε ε ρ
= =
=
;
,
The electric field distribution is defined by Poisson’s equation:
Electric field profile in the p-n junction
εεεε0 – the dielectric permittivity of vacuum;
εεεε0 = 8.85×10-12 F/m = 8.85×10-14 F/cm
εεεε −−−− relative dielectric permittivity of the material
In Si, εεεε ≈≈≈≈ 11.711.711.711.7

9. Charge, Field,
Potential Profiles in the
p-n junction
s
dF
dx
ρ
ε
= ; -2 -1
0
1 2
2
0
-2
-4
-6
p-type n-type
X

10. Charge, Field,
Potential Profiles in the
p-n junction
Using the depletion approximation, we obtain
dF
dx
=
−
qNa
εs
, for − xp < x < 0
qNd
εs
, for 0 < x < xn






s
dF
dx
ρ
ε
= ; -2 -1
0
1 2
2
0
-2
-4
-6
p-type n-type
-xp xn
X

11. Charge, Field,
Potential Profiles in the
p-n junction
Using the depletion approximation, we obtain
dF
dx
=
−
qNa
εs
, for − xp < x < 0
qNd
εs
, for 0 < x < xn






F =
−Fm 1+
x
xp





 , for − xp < x < 0
−Fm 1−
x
xn





 , for 0 < x < xn







-2 -1
0
1 2
2
0
-2
-4
-6
p-type n-type
-2 -1 0 1 2
0
-5
-10
-15
-2 -1 0 1 2
Distance (µm)
0.2
0
-0.2
-0.4
-0.6
-0.8
s
dF
dx
ρ
ε
= ;
-xp xn
-xp xn

12. On the p-side of the junction,
0
A
m p
qN
F x
εε
=
On the n-side of the junction,
0
D
m n
qN
F x
εε
=
At the junction interface: Fm(p-side) = Fm (n-side)
0 0
D A
m n p
qN qN
F x x
εε εε
= =
Maximum Field in the p-n junction
From
-2 -1 0 1 2
0
-5
-10
-15
-xp xn
s
dF
dx
ρ
ε
= :
p D
n A
x N
x N
=

13. 0 0
D A
m n p
qN qN
F x x
εε εε
= =
The voltage drop across the p-n junction, p nV F x dx− =−∫ ( )
= -{AREA UNDER the F(x) curve}
1
2
bi mV F W=
Voltage drop across the p-n junction
In equilibrium:
At reverse bias:
1
2bi r mV V F W− =
-2 -1 0 1 2
0
-5
-10
-15
-xp xn
W

14. 2 2
0 0 0
1
/ 2
2 1 / 2
D D D A
bi r n
D A A D
qN qN q N N
V V x W W W
N N N Nεε εε εε
 
− = = = 
+ + 
The total width of the depletion (space-charge) region.
W = xn + xp = xn (1 + ND/NA);
The voltage (the area of the triangle): Vbi –Vr = Fm× W/2;
Depletion region width in the p-n junction
p n D Ax x N N= ( / )From
W
Fm
0 0
D A
m n p
qN qN
F x x
εε εε
= =

15. Depletion region (a.k.a space-charge region) width
Depletion region of the p-n junction summary
2
02
D A
bi r
A D
N Nq
V V W N where N
N N
'; '
εε
 
− = = 
+ 
2
0
1
2A D bi r D
q
N N , V V N W
ε ε
>> − =
For strongly asymmetrical p-n junction:
2
0
1
2D A bi r A
q
N N , V V N W
ε ε
>> − =
The space-charge region is extended mainly to the low-doped side
of the p-n junction
Depletion region width sharing between n- and p-sides:
p n D Ax x N N( / )=W = xn + xp
W ≈ xn
W ≈ xp

16. From
Depletion region width as a function of voltage
2
02
bi r
q
V V W N '
εε
− =
( )02 bi rV V
W
qN
ε ε −
=
'
D A AFor N N , N N>> ='
The depletion region width W:
where
D A
A D
N N
N
N N
=
+
'
A D DFor N N , N N>> ='

17. Peak electric field in the p-n junction summary
Maximum electric field
1
2bi r mV V F W− =
( )
0
2 bi r
m
q N V V
F
'
ε ε
−
=
2
0
2
m
bi r
F
V V
q N '
ε ε
− =
2
0
2
BDF
V
q Nmax
'
ε ε
=

18. P-n Junction Breakdown

19. Avalanche Breakdown mechanism
Mechanisms for breakdown
Two quantum processes give rise to breakdown:
(1) Impact ionization plus avalanche multiplication.
(2) Quantum tunneling (Zener effect).
Relative importance depends on doping level in the p-
and n- regions:

20. Avalanche Breakdown mechanism
• Electric field accelerates electrons (and holes);
• The kinetic energy of electron in the electric field
increases;
• Electron with high enough excessive energy can ionize
the atom at collision.
• As a result, collision produces an electron-hole pair.

21. Avalanche Breakdown mechanism
Minimum additional electron energy required for
ionization can be estimated using:
0
2
2 G
mv
E≈
Additional electron energy comes from the electric field:
0
2
2 FP
mv
q F L≈
where F is the electric field and LFP is the “mean free path” – the
average distance that the electron passes between collisions.
From this, the ionization condition: BD FP Gq F L E≈
FBD is the critical or “breakdown” field.
The ionization only occurs if electric field exceeds the critical value

22. Breakdown in p-n junction
-2 -1 0 1 2
0
-5
-10
-15
-xp xn
In reverse-biased p-n junction, the electric field is concentrated
within a narrow depletion region.
The maximum electric field occurs exactly at the p-n interface.
As the field Fm exceeds the critical (breakdown) value:
Fm
Atome1
e1
e2h2

23. Avalanche multiplication during the breakdown
Ionization coefficient αe ≈ αh Ionization coefficient αe >> αh

24. Multiplication and Ionization Coefficients
Consider uniform electric field in the avalanche region
(for simplicity)
The avalanche region width is W
The condition for avalanching: (every carrier has one ionizing collision)
Assume αe = αh ≈ const (x);
Multiplication factor:
Numberof e h pairsattheoutput
M
Numberof e h pairsattheinput
−
=
−

25. Avalanche breakdown interpretation using band diagrams
EV
EC
p n
(1) Electrons from the p-side and holes from the n-
side get accelerated in the depletion regions by
strong electric filed
np
pn

26. EV
EC
p n
(2) At collision, electron produces new electron – hole
(e-h) pairs
Avalanche breakdown interpretation using band diagrams

27. EV
EC
p n
(3) These secondary e-h pairs in also acquire high energy and
may in turn produce more e-h pairs.
Avalanche breakdown interpretation using band diagrams

28. EV
EC
p n
(4) New electron hole pairs will add up to the reverse current
Avalanche breakdown interpretation using band diagrams

29. EV
EC
p n
(5) New electron-hole pairs will also create more electron
hole pairs (avalanche multiplication)
Avalanche breakdown interpretation using band diagrams

30. 2
2
s bd
abd
d
F
V
qN
ε
=
Breakdown voltage of the p-n junction
For a p+ - n junction
(NA >> ND):

31. Si p-n junction. Example 1:
Maximum Field vs. Reverse Voltage
0.0E+00
1.0E+05
2.0E+05
3.0E+05
4.0E+05
5.0E+05
6.0E+05
7.0E+05
8.0E+05
9.0E+05
1.0E+06
0 500 1000 1500 2000
Reverse Voltage, V
PeakElectricField,V/m
Fm
N = 1E15 cm
-3
FBD
( )
0
2 bi r
m
q N V V
F
'
ε ε
−
=

32. Si p-n junction. Example 2
Maximum Field vs. Doping
0.00E+00
2.00E+05
4.00E+05
6.00E+05
8.00E+05
1.00E+06
1.20E+06
1.40E+06
1.60E+06
0.00E+
00
1.00E+
15
2.00E+
15
3.00E+
15
4.00E+
15
5.00E+
15
6.00E+
15
7.00E+
15
Doping, cm-3
Fm,V/cm
V=1000 V
( )
0
2 bi r
m
q N V V
F
'
ε ε
−
=
FBD

33. Si p-n junction. Example 3
Maximum Voltage vs. Doping
0.00E+00
5.00E+02
1.00E+03
1.50E+03
2.00E+03
2.50E+03
0.00E
+00
1.00E
+15
2.00E
+15
3.00E
+15
4.00E
+15
5.00E
+15
6.00E
+15
7.00E
+15
8.00E
+15
Doping, cm-3
Vmax,V
2
0
2
BDF
V
q Nmax
'
ε ε
=
For Silicon,
FBD ≈ 3 ×105 V/cm

34. Zener (tunneling) breakdown
If the junction is highly doped then the depletion region can be very thin:
EV
EC
Thin junction (heavily doped)
( )02 bi rV V
W
qN
ε ε −
=
'
At high reverse bias, the conduction and valence bands on the opposite sides
of the junction are very close to each other

35. Zener (tunneling breakdown)
EV
EC
At certain reverse bias, the electrons from the valence band of p-material
can tunnel into the conductance band of n-material.
The reverse current increases abruptly at a certain voltage:
Typical voltage for the Zener breakdown, VZ ≈ 4 EG/q

36. Avalanche vs. Zener Breakdown comparison
Avalanche (100V – 5 kV)
Zener (5V – 10V)
I
V