Molecular Dynamics

Molecular Dynamics (Part 1)

Sparisoma Viridi*

Nuclear Physics and Biophysics Research Division
Institut Teknologi Bandung, Jalan Ganesha 10, Bandung 40132, Indonesia
*dudung@gmail.com

SK6202
Senin, 4 Februari 2013
1
BSC-A Lantai 3
Kapita Selekta Sains Komputasi

Outline
• Short history of molecular dynamics (MD)
• Introduction to MD
• MD Algorithm
• Example
• Assignments

SK6202
2
BSC-A Lantai 3

Short history

Molecular dynamics
Contribution from some works

SK6202
3
BSC-A Lantai 3

History of MD
• It was first introduced in studying the interact-
ions of hard spheres which exhibits phase
transitions (Alder et. al, 1957)
• Then, a series of paper led by Alder is then pu-
blished during 1959-1980 investigating this
method

B. J. Alder and T. E. Wainwright, “Phase Transition for a Hard Sphere System”, Journal of Chemical Physics 27 (5)
1208-1209 (1957)

SK6202
4
BSC-A Lantai 3

History of MD (cont.)
• Studies of Alder and Wainwright in 1957 and
1959 induced other studies concerning beha-
ior of simple liquids
• Realistic potential for liquid argon is then used
(Rahman, 1964)
• Simulation of realistic system is conducted for
the first time for water (Stillinger et. al, 1974)
A. Rahman, “Correlations in the Motion of Atoms in Liquid Argon”, Physical Review 136 (2A), A405-A411 (1964)
F. H. Stillinger and A. Rahman, “Improved Simulation of Liquid Water by Molecular Dynamics”, Journal of Chemical
Physics 60 (4), 1545-1557 (1974)

SK6202
5
BSC-A Lantai 3

History of MD (cont.)
• The dynamics of folded of globular protein
(bovine pancreatic trypsin inhibitor) is the first
protein simulation (McCammon et. al, 1977)
• Many program and code are released, e.g.
Chemistry HARvard Molecular Mechanics
(CHARMM) (Stote et. al, 1999)

J. A. McCammon, B. R. Gelin, and M. Karplus, “Dynamics of Folded Proteins”, Nature 267 (5612) 585-590 (1977)
R. Stote, A. Dejaegere, D. Kuznetsov, and L. Falquet, “Theory of Molecular Dynamcis Simulation ” in Tutori@l
Molecular Dynamics Simulation CHARMM, URI http://www.ch .embnet.org/MD_tutorial /pages/MD.Part1. html
[2012.02.13]
SK6202
6
BSC-A Lantai 3

Alder’s papers
• This series of papers published during 1959-
1980, a lot of time of consistency of studying
something
– I. General Method (1959)
– IV. Behavior of a Small Number of Elastic Spheres
(1960)
– III. A Mixture of Hard Spheres (1964)
– IV. The Pressure, Collision Rate, and Their Number
Dependence for Hard Disks (1967)
SK6202
7
BSC-A Lantai 3

Alder’s papers (cont.)
– V. High-Density Equation of State and Entropy for
Hard Disks and Spheres
– VI. Free-Path Distributions and Collision Rates for
Hard-Sphere and Square-Well Molecules (1968)
– VII. Hard-Sphere Distribution Functions and an
Augmented van der Waals Theory (1969)
– VIII. The Transport Coefficients for a Hard-Sphere
Fluid (1970)
– IX. Vacancies in Hard Sphere Crystals (1971)
SK6202
8
BSC-A Lantai 3

– X. Corrections to the Augmented van der Waals
Theory for the Square Well Fluid (1972)
– XI. Correlation Functions of a Hard-Sphere Test
Particle (1972)
– XII. Band Shape of the Depolarized Light Scattered
from Atomic Fluids (1973)
– XIII. Singlet and Pair Distribution Functions for
Hard-Disk and Hard-Sphere Solids (1974)

SK6202
9
BSC-A Lantai 3

– XIV. Mass and Size Dependence of the Binary
Diffusion Coefficient (1974)
– XV. High Temperature Description of the
Transport Coefficients (1975)
– XVI. Fluctuation Driven Resonance (1977)
– XVII. Phase diagrams for ’’step’’ potentials in two
and three dimensions (1979)
– XVIII. The square-well phase diagram (1980)

SK6202
10
BSC-A Lantai 3

Introduction

Molecular dynamics
Definitions, use, and limitations

SK6202
11
BSC-A Lantai 3

Molecular dynamics
• Molecular dynamics (MD) is a computer
simulation of physical movements of atoms
and molecules (Wikipedia, 2011)
• MD simulation consists of the numerical, step-
by-step, solution of classical equation of
motion (Allen, 2004)

Wikipedia contributors, “Molecular dynamics”, Wikipedia, The Free Encyclopedia, 5 September 2011, 15:49 UTC,
oldid:448597141 [2011.09.21]
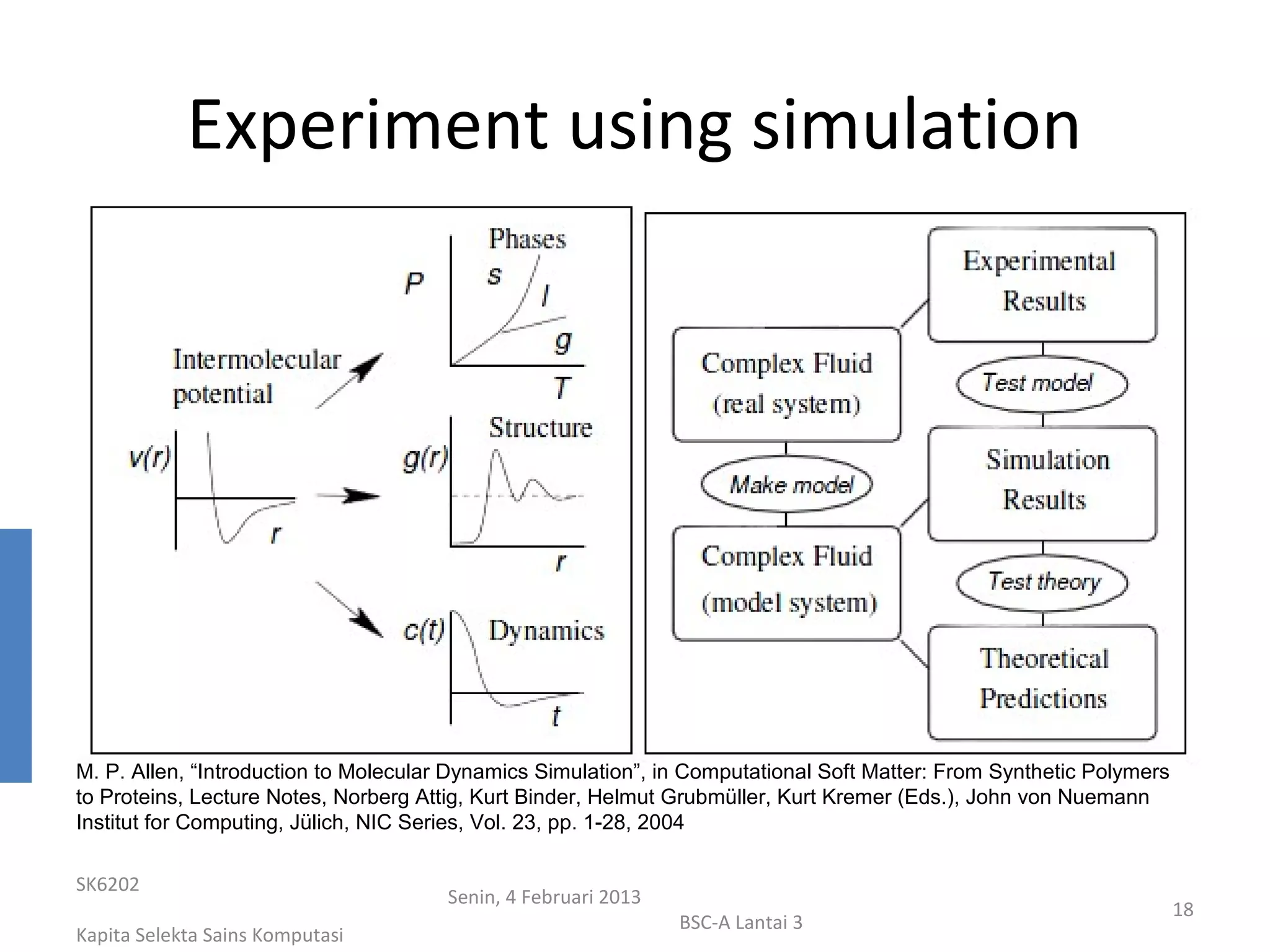
M. P. Allen, “Introduction to Molecular Dynamics Simulation”, in Computational Soft Matter: From Synthetic Polymers
to Proteins, Lecture Notes, Norberg Attig, Kurt Binder, Helmut Grubmüller, Kurt Kremer (Eds.), John von Nuemann
Institut for Computing, Jülich, NIC Series, Vol. 23, pp. 1-28, 2004
SK6202
12
BSC-A Lantai 3

Molecular dynamics (cont.)
• It is a computer simulation technique where
the time evolution of a set of interacting
atoms is followed by integrating their
equations of motion (Ercolessi, 1997)
• MD simulations can provide the ultimate
detail concerning individual motions as a
function of time (Karplus et. al, 2002)
F. Ercolessi, “A Molecular Dynamics Primer”, Spring College in Computational Physics, ICTP, Trieste, 9/10/1997 URI
http://www.fisica.uniud.it/~ercolessi/md /md/node6.html [2011.09.21]
M. Karplus and J. A. McCammon, “Molecular Dynamics Simulations of Biomolecules”, Nature Structural Biology 9 (9),
646-653 (2002)
SK6202
13
BSC-A Lantai 3

Range of use
• It is used from atomic until planetoid scale
• Calculation of electronic ground state as
function of time of liquid metal (Kresse et. al,
1993)
• Motion of n-Alkanes molecules (Ryckaert et.
al, 1977)

G. Kresse and J. Hafner, “Ab Initio Molecular Dynamics for Liquid Metals”, Physical Review B 47 (1), 558-561 (1993)
J. P. Ryckaert, G. Ciccotti, and H. J. C. Berendsen, “Numerical Integration of the Cartesian Equations of Motion of a
System with Constraints: Molecular Dynamics of n-Alkanes”, Journal of Computational Physics 23 (3), 327-341 (1977)

SK6202
14
BSC-A Lantai 3

Range of use (cont.)
• Nanodroplet on a surface (Sedighi et. al, 2010)
• Grains in mm and cm size (Gallas et. al, 1996)
• Simulation of asteroids movement (Jaffé et. al,
2002)

N, Sedighi, S. Murad, and S. K. Aggarwal, “Molecular Dynamics Simulations of Nanodroplet Spreading on Solid
Surfaces, Effect of Droplet Size”, Fluid Dynamics Research 42 (3), 035501 (2010)
J. A. C. Gallas, H. J. Herrmann, T. Pöschel, and Stefan Sokolowski, “Molecular Dynamics Simulation of Size
Segregation in Three Dimensions”, Journal of Statistical Physics 82 (1-2), 443-450 (1996)
C. Jaffé, S. D. Ross, M. W. Lo, J. Marsden, D. Farrelly, and T. Uzer, “Statistical Theory of Asteroid Escape Rates”,
SK6202
Physical Review Letters 89 (1), 011101 Senin, 4 Februari 2013
(2002)
15
BSC-A Lantai 3

Use of MD
• There are three main scenarios for the use of
MD (Fedman, 2006)
• In the first scenario the simulated properties
are compared with experimental results, and
when the two agree it is reasonable to claim
that the experimental results can be explained
by the simulation model.
F. Hedman, “Algorithms for Molecular Dynamics Simulations: Advancing the Computational Horizon”, Ph.D. Thesis,
Avdelningen för fysikalisk kemi, Arrheniuslaboratoriet, Stockholms Universitet, Stockholm, 2006

SK6202
16
BSC-A Lantai 3

Use of MD (cont.)
• In the second scenario, MD simulations are
used to interpret experimental results. In a
sense the second scenario is the inverse of the
first.
• In the third scenario, simulations are used as
an exploratory tool to help gain an initial
understanding of a problem and give guidance
among possible lines of investigation, be it
theoretical or experimental.
SK6202
17
BSC-A Lantai 3

Experiment using simulation

M. P. Allen, “Introduction to Molecular Dynamics Simulation”, in Computational Soft Matter: From Synthetic Polymers
to Proteins, Lecture Notes, Norberg Attig, Kurt Binder, Helmut Grubmüller, Kurt Kremer (Eds.), John von Nuemann
Institut for Computing, Jülich, NIC Series, Vol. 23, pp. 1-28, 2004

SK6202
18
BSC-A Lantai 3

Experiment .. simulation (cont.)
• It is a bridge between microscopic and
macroscopic
• It is also a bridge between theory and
experiment
• Do the experiment using simulation is a smart
way to reduce the financial problem
• Even all considered nature laws are input to
the system, it could give the unexpected
SK6202
19
BSC-A Lantai 3

Is MD so perfect?
• Unfortunately not
• It has problem even all forces are already
considered
• It can produce unreported results or
unexpected (wrong) results
• It has problem in time stamp

SK6202
20
BSC-A Lantai 3

Time stamp problem
• Nanodroplet

N, Sedighi, S. Murad, and S. K. Aggarwal, “Molecular Dynamics Simulations of Nanodroplet Spreading on Solid
Surfaces, Effect of Droplet Size”, Fluid Dynamics Research 42 (3), 035501 (2010)

SK6202
21
BSC-A Lantai 3

Time stamp problem (cont.)

SK6202
22
BSC-A Lantai 3

• Granular oscillation

K. -C. Chen, C. -H. Lin, C. -C. Li, and J. -J. Li, “Dual Granular Temperature Oscillation of a Compartmentalized
Bidisperse Granular Gas”, Journal of the Physical Society of Japan 78 (4), 044401 (2009)

SK6202
23
BSC-A Lantai 3


SK6202
24
BSC-A Lantai 3

MD Algorithm

Trajectory of a particle
Potentials, the forms, and their physical meaning

SK6202
25
BSC-A Lantai 3

Algorithms
• It is uses Newton’s second law of motion to
get the acceleration a
• It using numerical integration to get the
equation of motion, use the simple method
i.e. original Euler method
• New motion parameters will cause new value
of all forces
• Calculate the new forces to get new a
SK6202
26
BSC-A Lantai 3

Algorithms (cont.)
• Newton’s second law of motion
 
∑ F = ma

• Left side consists of all considered forces

SK6202
27
BSC-A Lantai 3

Algorithms (cont.)
• Euler method:
  
vi +1 = vi + ai ∆t
  
ri + 1 = ri + vi ∆t

t i +1 = t i + ∆t

• Particle position is given by ri at time t i

SK6202
28
BSC-A Lantai 3

Algorithms (cont.)
• You must pay attention to influence from out-
side of the system that changed with order of
magnitude of chosen Δt
• Normally it is chosen that Δt must be 100
times smaller than that change

SK6202
29
BSC-A Lantai 3

Potentials
• Lennard-Jones potential
 σ 12  σ  6 
U LJ ( r ) = 4ε   −   
 r 
 r  

• Coulomb potential
q1q 2 1
UC (r) =
4πε 0 r
SK6202
30
BSC-A Lantai 3

Potentials (cont.)
• Gravitation potensial near large object
U G ( r ) = −mgr

• Gravitation potensial
1
U G ( r ) = −Gm1m2
r
SK6202
31
BSC-A Lantai 3

Potentials (cont.)
• Morse potential

U M ( r ) = De 1 − e [ ]
−α ( r − re ) 2

• Yukawa potential
− kmr
e
U Y ( r) = −g 2

r
SK6202
32
BSC-A Lantai 3

Potentials (cont.)
• Harmonic oscillator potential
1
U HO ( r ) = k ( r − r0 )
2

2

SK6202
33
BSC-A Lantai 3

Force
• Force can be obtained from potential through
 
F = −∇U

SK6202
34
BSC-A Lantai 3

Granular memory device

Example
Sequence of particle under gravitation potential

SK6202
35
BSC-A Lantai 3

System
• Granular device (D), sensor (S), particle
sequence (P)

• P moves with constant initial velocity before
entering D
SK6202
36
BSC-A Lantai 3

Typical states
• Observed states are:
– s10w0r0 (two configurations)
– s10w1r0
– s10w1r1

SK6202
37
BSC-A Lantai 3

Typical states (cont.)
• Writing zero particle and relecting none from
ten particles sequence (s10w0r0)

• gn = 0, gp = 0, b = 0, v0 = 4

SK6202
38
BSC-A Lantai 3

• Writing zero particle and relecting none from

• gn = 1, gp = -2, b = 2, v0 = 6

SK6202
39
BSC-A Lantai 3

• Writing one particle and relecting none from

• gn = 1, gp = -2, b = 2, v0 = 5

SK6202
40
BSC-A Lantai 3

• Writing one particle and relecting another one
from ten particles sequence (s10w1r1)

• gn = 1, gp = -3, b = 2, v0 = 4

SK6202
41
BSC-A Lantai 3

Assignments

SK6202
42
BSC-A Lantai 3

Assignments
• Make six groups of 2-3 students
• Each group collects only one answer file
• Answer file should be sent to
dudung@gmail.com with subject [SK6202] MD
Assignment 1
• The file sould be received before 11 February
2013

SK6202
43
BSC-A Lantai 3

Assignments (cont.)
• Question 1. Derive force formulation for
following potential:
(a) harmonic oscillator,
(b) Coulomb,
(c) gravitation,
(d) Lennard-Jones,
(e) Morse,
(f) Yukawa
SK6202
44
BSC-A Lantai 3

Assignments (cont.)
• Question 2. Describe the physical meaning of
parameters used in each force or potential
formulation
• Question 3. Tell the difference between
molecular dynamics and molecular mechanics
• Question 4. Find the Euler, Verlet, Gear pre-
dictor-corrector, Rattle, and Shake algorithm
• Question 5. Find a topic to be solved using
molecular dynamics and explain
SK6202
45
BSC-A Lantai 3

Thank you

SK6202
46
BSC-A Lantai 3

Molecular Dynamics

More Related Content

What's hot

Viewers also liked

More from Sparisoma Viridi

Recently uploaded

Molecular Dynamics