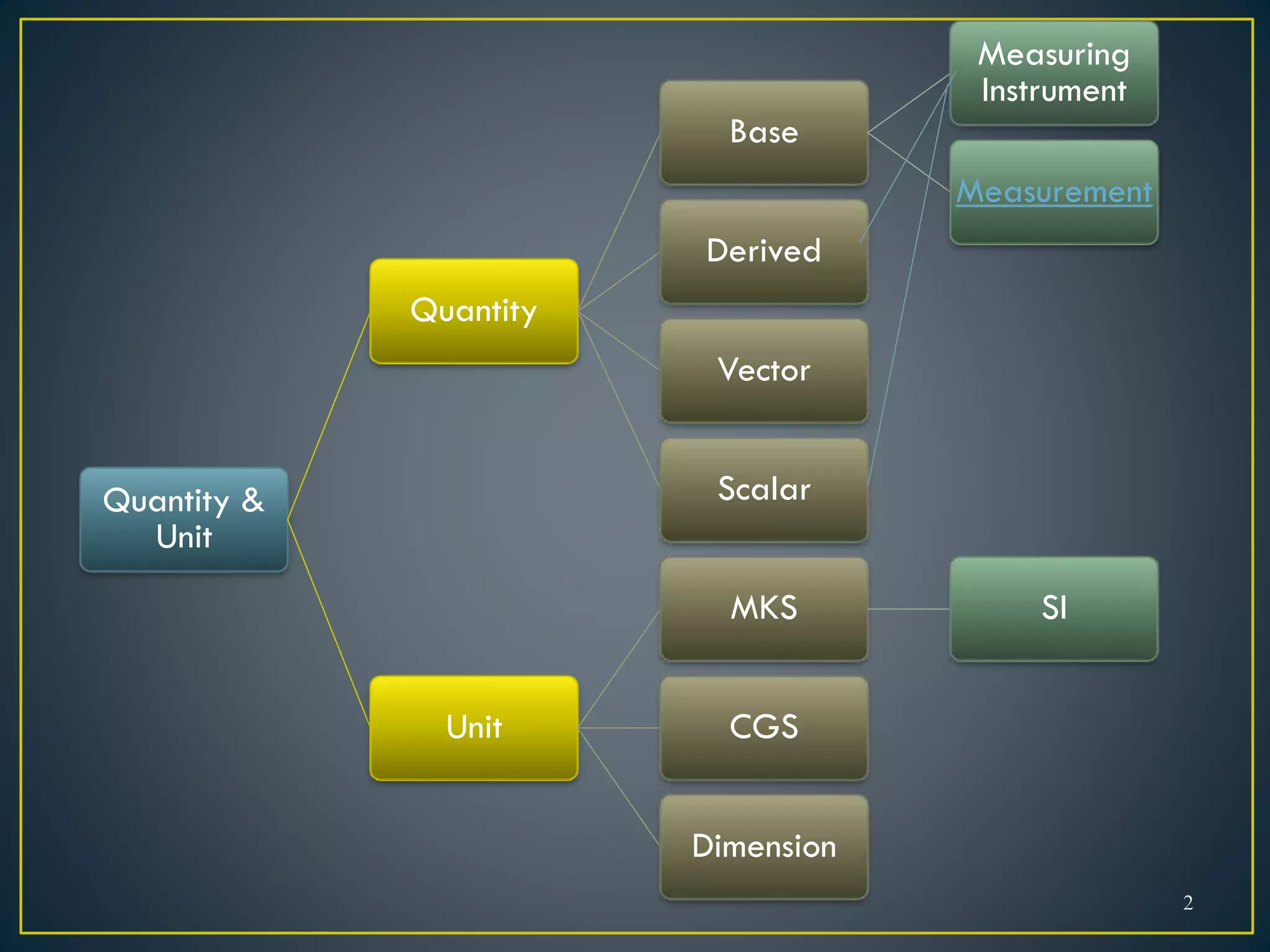
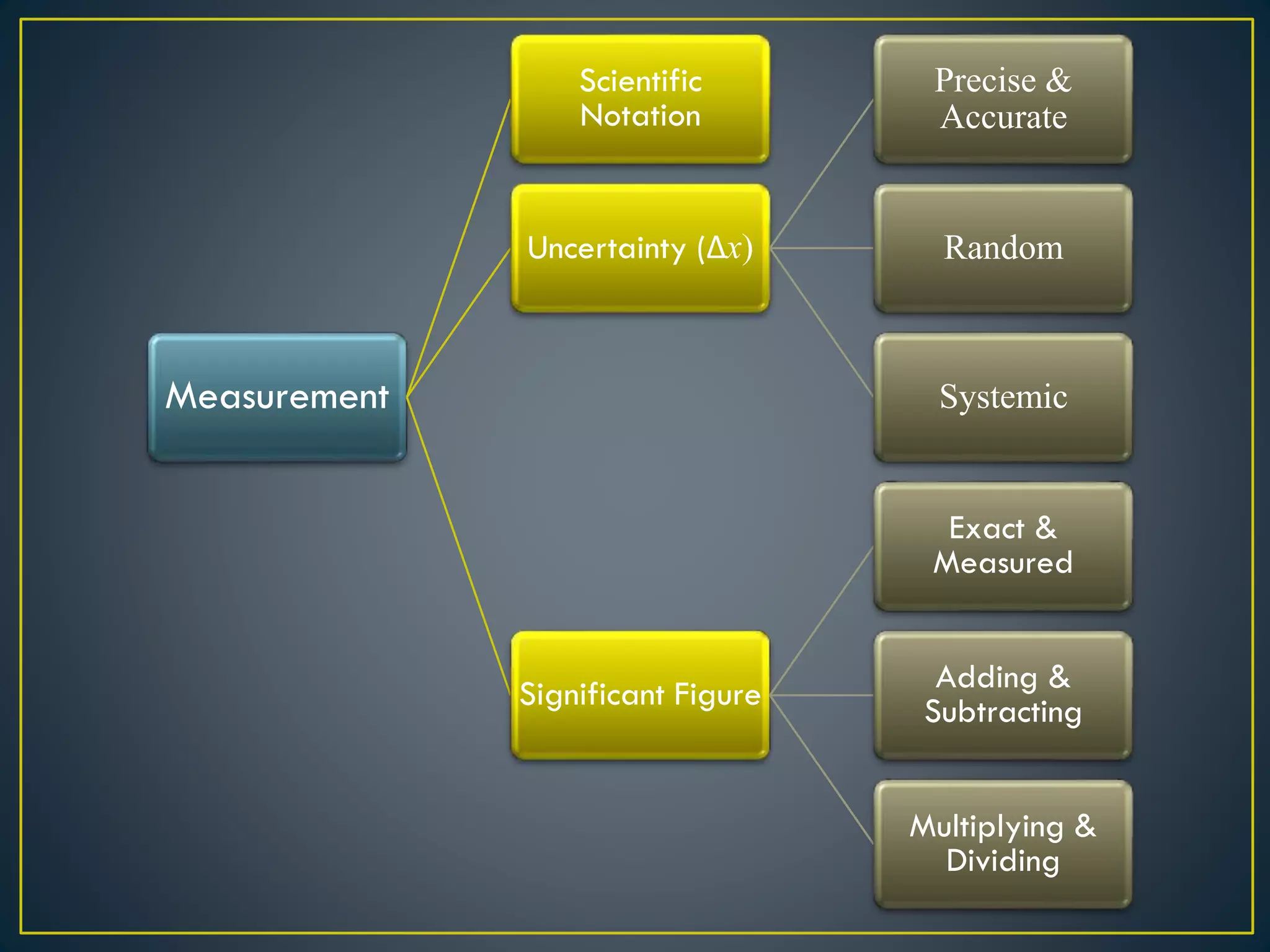
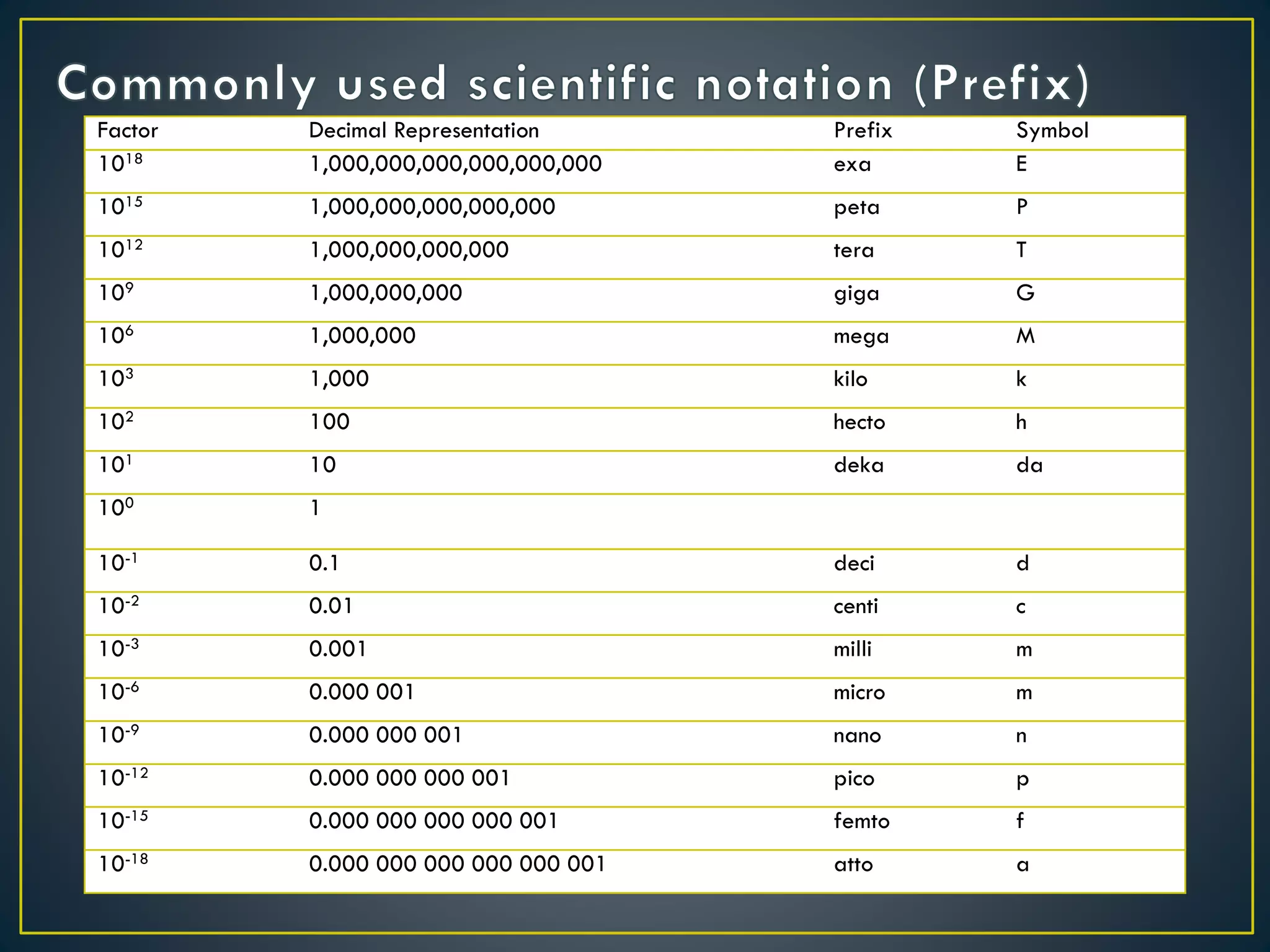
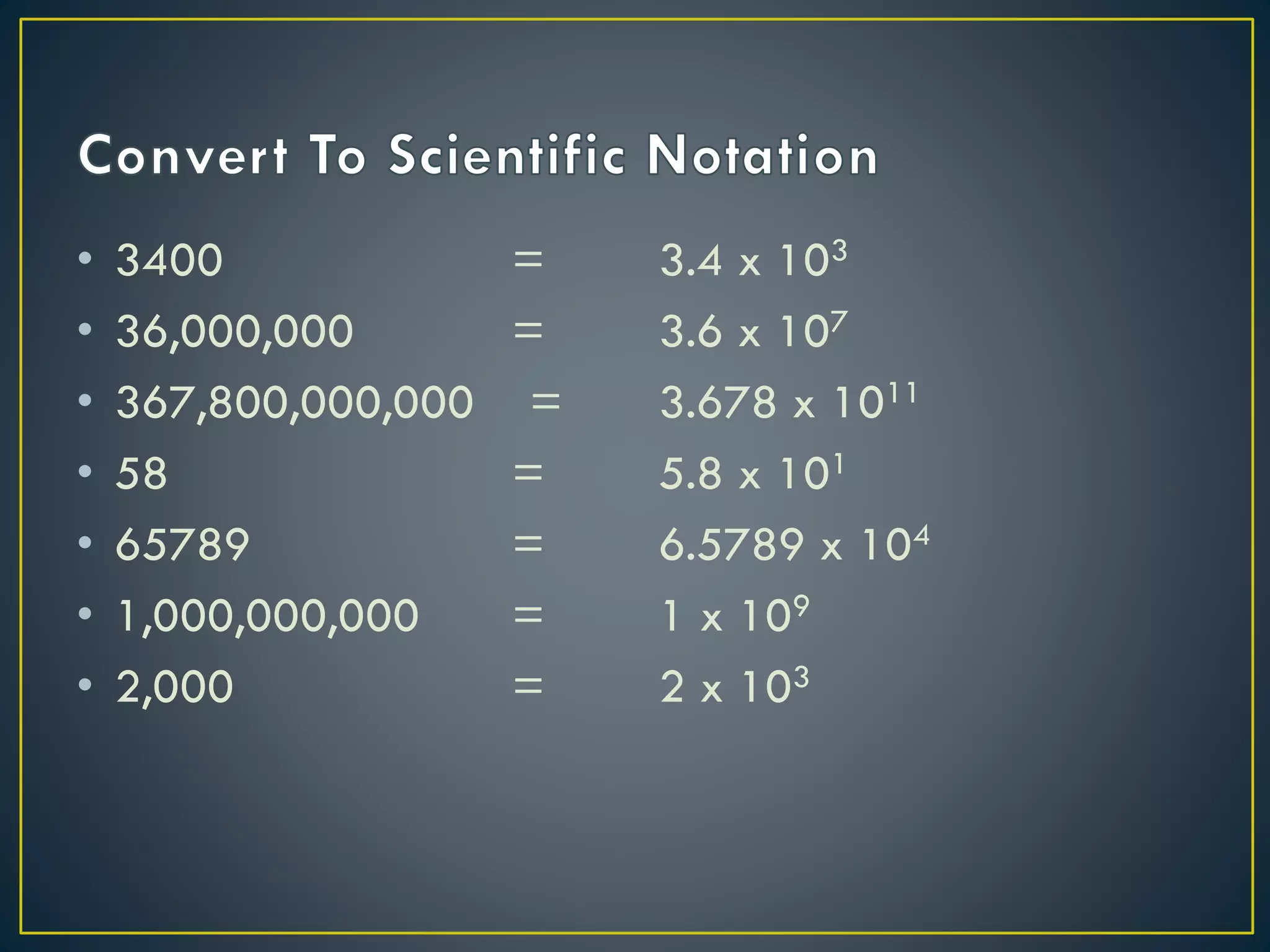
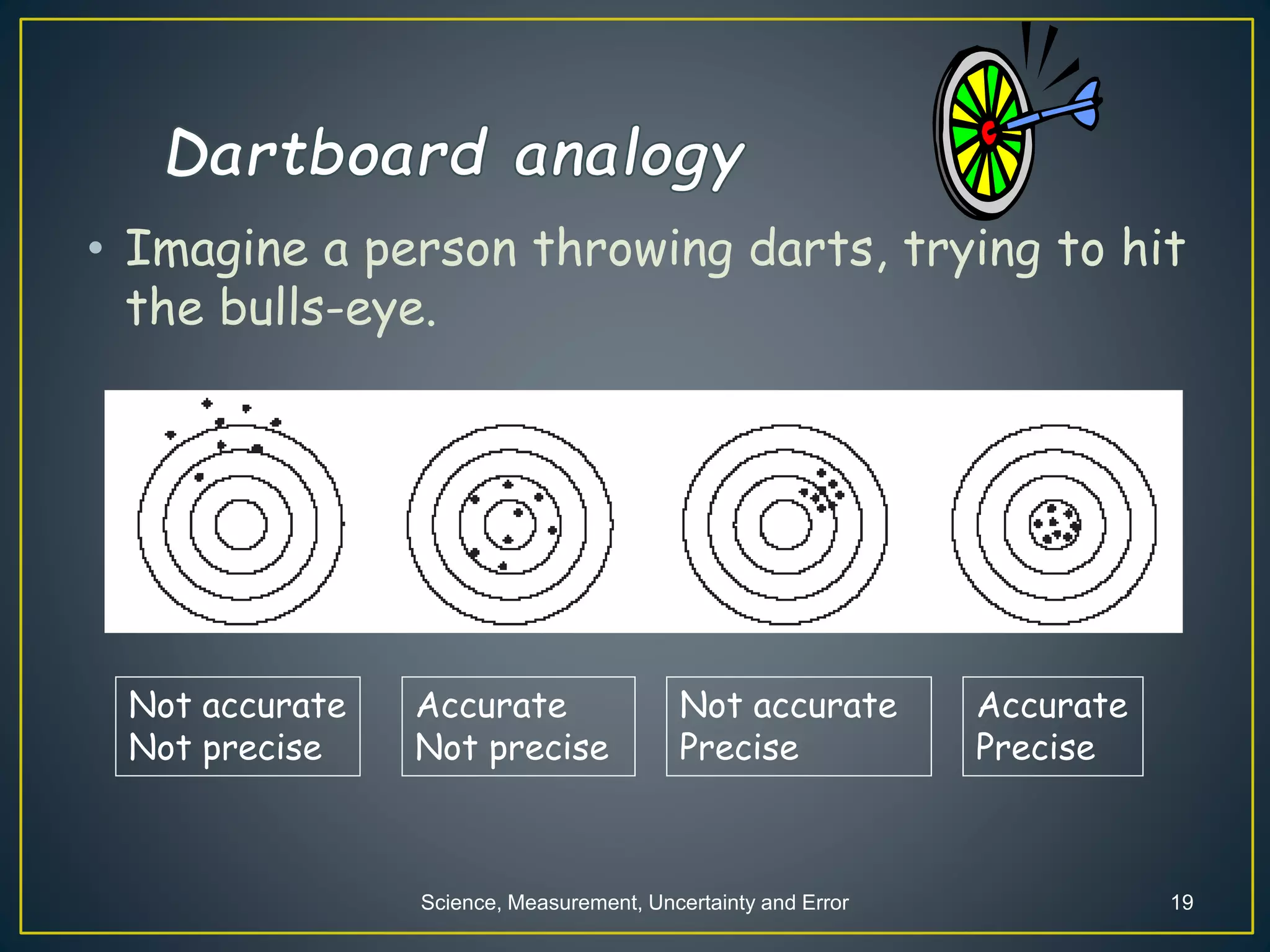
- Scientific notation is a way of writing very large or small numbers as a product of a number between 1 and 10 and a power of 10. - Prefixes are used to indicate the power of 10 being multiplied, with examples including mega (106) and micro (10-6). - When measuring quantities, only a certain number of digits can be known with certainty based on the precision of the measuring instrument. Significant figures indicate the digits that are known precisely.

2. Quantity &
Unit
Quantity
Base
Measuring
Instrument
Measurement
Derived
Vector
Scalar
Unit
MKS SI
CGS
Dimension
2

3. Measurement
Scientific
Notation
Uncertainty (Δx)
Precise &
Accurate
Random
Systemic
Significant Figure
Exact &
Measured
Adding &
Subtracting
Multiplying &
Dividing

4. • Scientific notation is a convenient way to write a very
small or a very large number.
• Numbers are written as a product of a number
between 1 and 10, times the number 10 raised to
power.
• 215 is written in scientific notation as:
215 = 2.15 x 100 = 2.15 x (10 x 10) = 2.15 x 102
Chapter Two 4

5. • Alternative writing method
• Using standard form
• N × 10n where 1  N < 10 and n is an integer
This galaxy is about 2.5 × 106
light years from the Earth.
The diameter of this atom
is about 1 × 10−10 m.

6. Factor Decimal Representation Prefix Symbol
1018 1,000,000,000,000,000,000 exa E
1015 1,000,000,000,000,000 peta P
1012 1,000,000,000,000 tera T
109 1,000,000,000 giga G
106 1,000,000 mega M
103 1,000 kilo k
102 100 hecto h
101 10 deka da
100 1
10-1 0.1 deci d
10-2 0.01 centi c
10-3 0.001 milli m
10-6 0.000 001 micro m
10-9 0.000 000 001 nano n
10-12 0.000 000 000 001 pico p
10-15 0.000 000 000 000 001 femto f
10-18 0.000 000 000 000 000 001 atto a

7. Chapter Two 7
Two examples of converting standard notation to
scientific notation are shown below.

8. Chapter Two 8

9. • 0.00034 =
• 0.00145 =
• 0.0000985 =
• 0.016856 =
• 0.0003967 =
• 0.0000002 =
• 0.00040 =
• 0.00600 =
3.4 x 10 4
1.45 x 10 3
9.85 x 10 5
1.6856 x 10 2
3.967 x 10 4
2 x 10 7
4.0 x 10 4
6.00 x 10 3

10. • 3400 =
• 36,000,000 =
• 367,800,000,000 =
• 58 =
• 65789 =
• 1,000,000,000 =
• 2,000 =
3.4 x 103
3.6 x 107
3.678 x 1011
5.8 x 101
6.5789 x 104
1 x 109
2 x 103

11. • 7.4 x 103 =
• 5.6 x 105 =
• 6.674 x 1010 =
• 5.1 x 104 =
• 6.5559 x 101 =
• 3.64186 x 104 =
• 1 x 103 =
7,400
560,000
66,740,000,000
51,000
65.559
36,418.6
1,000

12. • 7.4 x 103 =
• 5.6 x 105 =
• 6.674 x 108 =
• 5.1 x 104 =
• 6.5559 x 101 =
• 3.641 x 104 =
• 1 x 103 =
0.0074
0.000056
0.00000006674
0.00051
0.65559
0.0003641
0.001

13. 5/12/2016 Chapter Two 13
Convert the following quantities to their SI unit.
a. 510 nm
510 nm = (510 x 10−9
) m
= 51 x 10−8
m
= 5.1 x 10−7 m
= 5.10 x 10−7
m
= 5.100 x 10−7 m
b. 2,3 mm
c. 78 MHz

14. Chapter Two 14
• Scientific notation is helpful for indicating how many significant
figures are present in a number that has zeros at the end but
to the left of a decimal point.
• The distance from the Earth to the Sun is 150,000,000 km.
Written in standard notation this number could have anywhere
from 2 to 9 significant figures.
• Scientific notation can indicate how many digits are significant.
Writing 150,000,000 as 1.5 x 108 indicates 2 and writing it
as 1.500 x 108 indicates 4.
• Scientific notation can make doing arithmetic easier. Rules for
doing arithmetic with numbers written in scientific notation are
reviewed in Appendix A.

15. Science, Measurement, Uncertainty and Error 15
The precision and
accuracy are
limited by the
instrumentation
and data gathering
techniques.
Scientists always want the
most precise and accurate
experimental data.

16. Science, Measurement, Uncertainty and Error 16
• No matter how good
you are… there will
always be errors.
• This error in
measurement is called
as uncertainties
• The uncertainties are
the natural behavior in
a measurements

17. Science, Measurement, Uncertainty and Error 17
• Identify the errors and their magnitude.
• Try to reduce the magnitude of the
error.
HOW?
• Better instruments
• Better experimental design
• Collect a lot of data

18. Science, Measurement, Uncertainty and Error 18
• Precision
How reproducible are
measurements?
• Accuracy
How close are the
measurements to the true
value.

19. Science, Measurement, Uncertainty and Error 19
• Imagine a person throwing darts, trying to hit
the bulls-eye.
Not accurate
Not precise
Accurate
Not precise
Not accurate
Precise
Accurate
Precise

20. • Random Uncertainties
a. Different People
b. Measurement Equipment
c. Different Measurement Result
• Systemic Uncertainties, it is caused by the measurement
equipment has never been calibrated
Science, Measurement, Uncertainty and Error 20

21. • There are 2 different types of numbers
• Exact
• Measured
• Exact numbers are infinitely important
• Measured number = they are measured with a measuring
device (name all 4) so these numbers have ERROR.
21

22. An exact number is obtained when you count objects or use a
defined relationship.
22
Counting objects are always exact
2 soccer balls
4 pizzas
Exact relationships, predefined values, not measured
1 foot = 12 inches
1 meter = 100 cm
For instance is 1 foot = 12.000000000001 inches? No
1 ft is EXACTLY 12 inches.

23. • Every experimental
measurement has a degree
of uncertainty.
• The volume, V, at right is
certain in the 10’s place,
10mL<V<20mL
• The 1’s digit is also certain,
17mL<V<18mL
• A best guess is needed for
the tenths place.
Chapter Two 23

24. • We can see the markings between 1.6-1.7cm
• We can’t see the markings between the .6-.7
• We must guess between .6 & .7
• We record 1.67 cm as our measurement
• The last digit an 7 was our guess...stop there
24
1 2 3 4 cm

25. What is the length of the wooden stick?
1) 4.5 cm
2) 4.54 cm
3) 4.547 cm

26. • Do you see why Measured Numbers have error…you have to
make that Guess!
• All but one of the significant figures are known with certainty.
The last significant figure is only the best possible estimate.
• To indicate the precision of a measurement, the value
recorded should use all the digits known with certainty.
26

27. Chapter Two 27
Below are two measurements of the mass of the
same object. The same quantity is being described
at two different levels of precision or certainty.

28. When reading a measured value, all nonzero digits should be
counted as significant. There is a set of rules for determining if
a zero in a measurement is significant or not.
• RULE 1. Zeros in the middle of a number are like any other
digit; they are always significant.
94.072 g has five significant figures.
• RULE 2. Zeros at the beginning of a number are not
significant; they act only to locate the decimal point.
0.0834 cm has three significant figures
0.029 07 mL has four.
Chapter Two 28

29. • RULE 3. Zeros at the end of a number and after the
decimal point are significant. It is assumed that these zeros
would not be shown unless they were significant.
138.200 m has six significant figures.
If the value were known to only four significant figures,
we would write 138.2 m.
• RULE 4. Zeros at the end of a number and before an
implied decimal point may or may not be significant. We
cannot tell whether they are part of the measurement or
whether they act only to locate the unwritten but implied
decimal point.
1000 g has 1 significant figure
1000 g has two sigure figure
Chapter Two 29

30. Practice Rule #1 Zeros
45.8736
0.000239
0.00023900
48000.
48000
3.982106
1.00040
6
3
5
5
2
4
6
•All digits count
•Leading 0’s don’t
•Trailing 0’s do
•0’s count in decimal form
•0’s don’t count w/o decimal
•All digits count
•0’s between digits count as well
as trailing in decimal form

31. 1. 2.83
2. 36.77
3. 14.0
4. 0.0033
5. 0.02
6. 0.2410
7. 2.350 x 10–2
8. 1.00009
9. 3
10. 0.0056040
3
4
3
2
1
4
4
6
infinite
5

32. • Often when doing arithmetic on a pocket calculator, the
answer is displayed with more significant figures than are
really justified.
• How do you decide how many digits to keep?
• Simple rules exist to tell you how.
Chapter Two 32

33. • Once you decide how many digits to retain, the rules for
rounding off numbers are straightforward:
• RULE 1. If the first digit you remove is 4 or less, drop it and all
following digits. 2.4271 becomes 2.4 when rounded off to
two significant figures because the first dropped digit (a 2) is
4 or less.
• RULE 2. If the first digit removed is 5 or greater, round up by
adding 1 to the last digit kept. 4.5832 is 4.6 when rounded
off to 2 significant figures since the first dropped digit (an 8)
is 5 or greater.
• If a calculation has several steps, it is best to round off at the
end.
Chapter Two 33

34. Make the following into a 3 Sig Fig number
1.5587
.0037421
1367
128,522
1.6683 106
1.56
.00374
1370
129,000
1.67 106
Your Final number
must be of the same
value as the number
you started with,
129,000 and not 129

35. For example you want a 4 Sig Fig number
4965.03
780,582
1999.5
0 is dropped, it is <5
8 is dropped, it is >5; Note you
must include the 0’s
5 is dropped it is = 5; note you
need a 4 Sig Fig
4965
780,600
2000.

36. RULE 1. In carrying out a multiplication or division, the answer
cannot have more significant figures than either of the original
numbers.
Chapter Two 36

37. •RULE 2. In carrying out an addition or subtraction, the
answer cannot have more digits after the decimal point
than either of the original numbers.
Chapter Two 37

38. 32.27  1.54 = 49.6958
3.68  .07925 = 46.4353312
1.750  .0342000 = 0.05985
3.2650106  4.858 = 1.586137  107
6.0221023  1.66110-24 = 1.000000
49.7
46.4
.05985
1.586 107
1.000

39. 25.5 32.72 320
+34.270 - 0.0049 + 12.5
59.770 32.7151 332.5
59.8 32.72 330

40. __ ___ __.56 + .153 = .713
82000 + 5.32 = 82005.32
10.0 - 9.8742 = .12580
10 – 9.8742 = .12580
.71
82000
.1
0
Look for the
last important
digit

41. 8.52 + 4.1586  18.73 + 153.2 =

42. 8.52 + 4.1586  18.73 + 153.2 =
(8.52 + 4.1586)  (18.73 + 153.2) =
239.6
2180.
= 8.52 + 77.89 + 153.2 = 239.61 =
= 12.68  171.9 = 2179.692 =