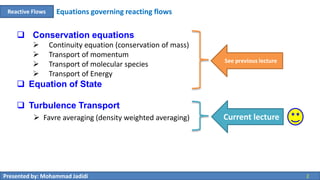
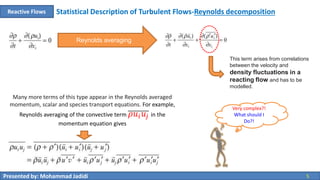
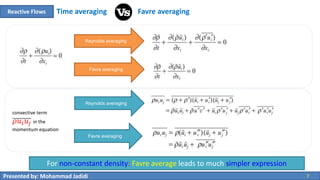
This document discusses reactive flow modeling in combustion chambers. It covers the equations governing reacting flows, including conservation equations for mass, momentum, molecular species, and energy. It also discusses the equation of state and turbulence transport. The document then covers statistical descriptions of turbulent flows using Reynolds decomposition and Favre averaging. Favre averaging is preferred for reacting flows with variable density as it leads to simpler expressions in the transport equations for continuity, momentum, species, and energy compared to Reynolds averaging. Various terms that arise in the averaged equations require turbulence modeling approaches.

1. Reactive Flows
Dr. Mohammad Jadidi
(Ph.D. in Mechanical Engineering)
Reactive flow modeling in combustion chamber

2. Presented by: Mohammad Jadidi 2
Equations governing reacting flowsReactive Flows
 Conservation equations
 Continuity equation (conservation of mass)
 Transport of momentum
 Transport of molecular species
 Transport of Energy
 Equation of State
 Turbulence Transport
See previous lecture
Current lecture Favre averaging (density weighted averaging)

3. Presented by: Mohammad Jadidi 3
Statistical Description of Turbulent Flows-Reynolds decompositionReactive Flows

4. Presented by: Mohammad Jadidi 4
Reactive Flows Statistical Description of Turbulent Flows-Reynolds decomposition

5. Presented by: Mohammad Jadidi 5
Reactive Flows
This term arises from correlations
between the velocity and
density fluctuations in a
reacting flow and has to be
modelled.
Many more terms of this type appear in the Reynolds averaged
momentum, scalar and species transport equations. For example,
Reynolds averaging of the convective term 𝜌𝑢𝑖 𝑢𝑗 in the
momentum equation gives
Very complex?!
What should I
Do?!
Reynolds averaging
Statistical Description of Turbulent Flows-Reynolds decomposition

6. Presented by: Mohammad Jadidi 6
Reactive Flows
To reduce the number of separate terms requiring modelling in reacting flows with variable
density, we use a density-weighted averaging procedure known as Favre averaging
Statistical Description of Turbulent Flows-Favre averaging

7. For non-constant density: Favre average leads to much simpler expression
Presented by: Mohammad Jadidi 7
Time averaging Favre averagingReactive Flows
Favre averaging
Reynolds averaging
convective term
𝜌𝑢𝑖 𝑢𝑗 in the
momentum equation
Favre averaging
Reynolds averaging

8. Presented by: Mohammad Jadidi 8
Reactive Flows Time averaging Favre averaging

9. Presented by: Mohammad Jadidi 9
Reactive Flows
Continuity
It should be noted that density in combusting flows is a variable,
and depends on pressure, temperature and species concentration.
Momentum equations
This term needs modeling.This term needs modeling.
Statistical Description of Turbulent Flows-Favre averaging

10. Turbulence viscosity assumption
proposed by Boussinesq
Presented by: Mohammad Jadidi 10
Reactive Flows
𝑘 =
1
2
𝑘=1
3
𝑢 𝑘
"
𝑢 𝑘
"
𝜀 = 𝜐
𝜕𝑢𝑖
"
𝜕𝑥𝑗
𝜕𝑢𝑖
"
𝜕𝑥𝑗
Statistical Description of Turbulent Flows-Favre averaging

11. Presented by: Mohammad Jadidi 11
Reactive Flows
Transport equations for species (k)
This term needs modeling
Favre-averaged
reactionrate
Again applying gradient
diffusion assumption gives
𝛔 𝐤 turbulent Schmidt
number for species 𝐤
where
Statistical Description of Turbulent Flows-Favre averaging

12. Presented by: Mohammad Jadidi 12
Reactive Flows
Energy equation
Statistical Description of Turbulent Flows-Favre averaging

13. 13
Thanks
Next part:
Reactive Flows
https://ir.linkedin.com/in/moammad-jadidi-03ab8399
Jadidi.cfd@gmail.com
Dr. Mohammad Jadidi
(Ph.D. in Mechanical Engineering)
https://www.researchgate.net/profile/Mohammad_Jadidi
https://www.slideshare.net/MohammadJadidi