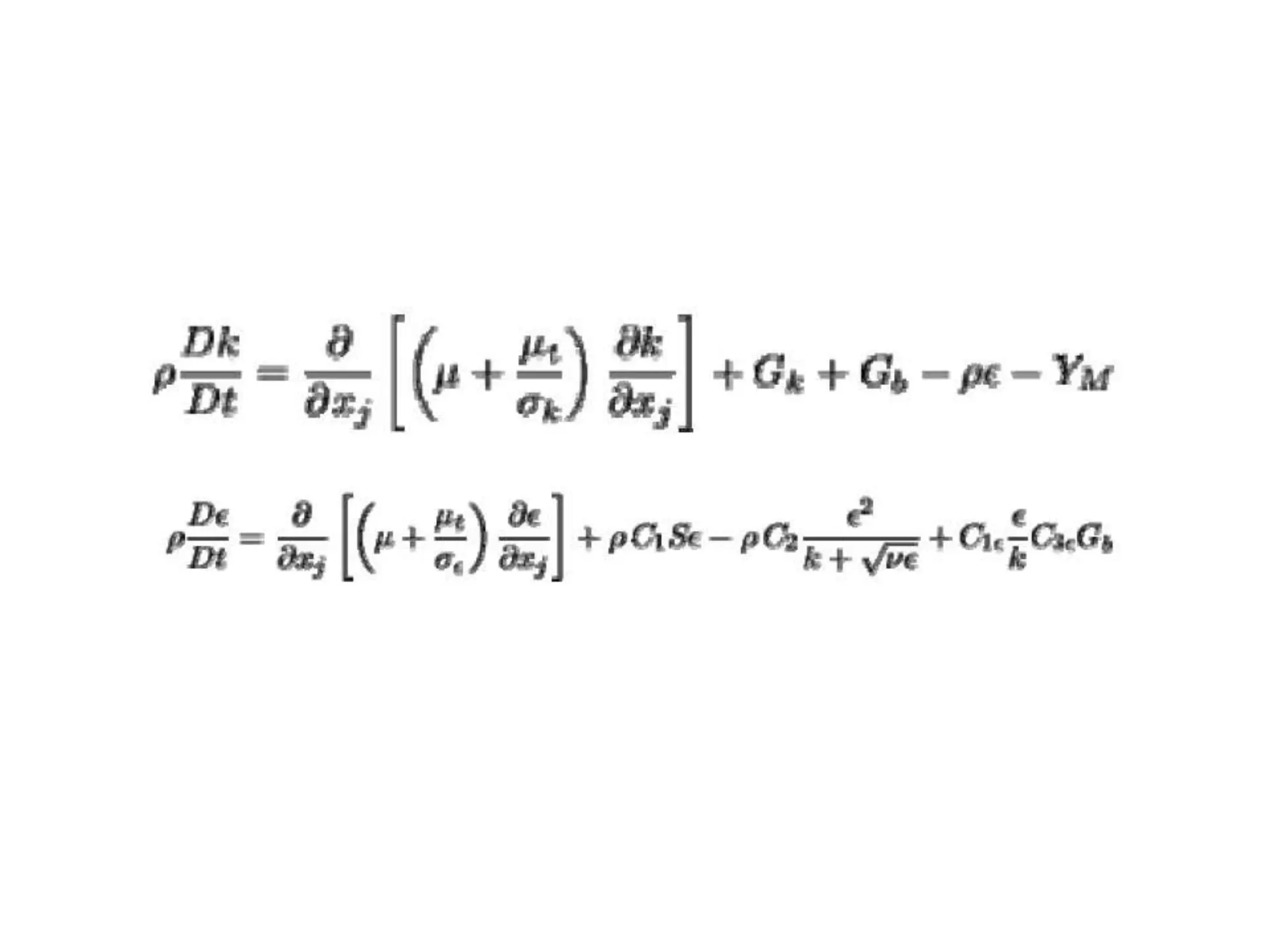The document summarizes three turbulence models: the standard k-ε model, RNG k-ε model, and realizable k-ε model. The major differences between the models are their methods of calculating turbulent viscosity, turbulent Prandtl numbers, and generation/destruction terms. Some features are similar between the models, including turbulent production, buoyancy effects, and modeling heat/mass transfer. The realizable k-ε model addresses deficiencies of previous models like predicting round jet spreading rates. Buoyancy effects are included in all three models through modifications to the turbulent kinetic energy generation term.

1. The Standard, RNG, and Realizable
k-
Models

2. • The major
differences in the models are as follows:
• the method of calculating turbulent
viscosity
• the turbulent Prandtl numbers
governing the turbulent diffusion of k
and
• the generation and destruction terms in
the equation

3. • i-the transport equations,
• ii-methods of calculating turbulent
viscosity, and
• iii-) model constants
are presented separately for each model.

4. The following features are almost
same.
• i-turbulent production,
• ii- generation due to buoyancy,
• iii-accounting for the effects of
compressibility,
• iv-modeling heat and mass transfer.

5. Standart k-ε Model
• In the derivation of the k- model, it was
assumed that the flow is fully turbulent,
and the effects of molecular viscosity are
negligible.
The standard k- model is therefore valid
only for fully turbulent flows.

6. • The turbulent kinetic energy, k, and its rate
of dissipation, ε

7. • Gk represents the generation of turbulent
kinetic energy due to the mean velocity
gradients.
Gb is the generation of turbulent kinetic
energy due to buoyancy.
YM represents the contribution of the
fluctuating dilatation in compressible
turbulence to the overall dissipation rate.

9. • These default values have been determined
from experiments with air and water for
fundamental turbulent shear flows
including homogeneous shear flows and
decaying isotropic grid turbulence. !!!
They have been found to work fairly well
for a wide range of wall-bounded and free
shear flows.

10. The RNG k-ε Model
• instantaneous Navier-
Stokes equations, using a mathematical
technique called ``renormalization group''

11. The quantities αk and αεare the inverse
effective Prandtl numbers for k and ,
respectively.

12. Modeling the effective viscosity

13. • Equation
is integrated to obtain an accurate
description of how the effective turbulent
transport varies with the effective
Reynolds number (or eddy scale),
allowing the model to better handle low-
Reynolds-number and near-wall flows .

14. • In the high-Reynolds-number limit, this
equation gives

15. RNG Swirl Modification
• Turbulence, in general, is affected by
rotation or swirl in the mean flow. The
RNG model provides an option to account
for the effects of swirl or rotation by
modifying the turbulent viscosity

19. • The main difference between the RNG and
standard k- models lies in the additional
term in the equation given by

22. In rapidly strained flows, the
RNG model yields a lower turbulent
viscosity than the standard k- model

23. • Thus, the RNG model is more responsive
to the effects of rapid strain and streamline
curvature than the standard k- model,
which explains the superior performance of
the RNG model for certain classes of
flows.

24. The Realizable k- Model
• In addition to the standard and RNG-based
k-ε models described there is also the so called
realizable k- ε model.
• The term ``realizable'' means that the
model satisfies certain mathematical
constraints on the normal stresses,
consistent with the physics of turbulent
flows.

25. • To understand this, consider combining the
• Boussinesq relationship and the eddy
viscosity definition to obtain the following
expression for the normal Reynolds stress
in an in compressible strained mean flow:

27. The well-known round-jet anomaly (named based on the finding that
the spreading rate in planar jets is predicted reasonably well,
but prediction of the spreading rate for axisymmetric jets (round) is
unexpectedly poor) is considered to be mainly due to the
modeled dissipation equation.

28. • The realizable k- model was intended to
address these deficiencies:

30. • the form of the equation is quite
different from those in the standard and
RNG-based k- models.

32. • ii- Another desirable feature is that the
destruction term does not have any
singularity; i.e., its denominator never vanishes,
even if k vanishes or becomes
smaller than zero. This feature is
contrasted with traditional k- models,
which have a singularity due to k in the
denominator.

33. Realizable k-ε model has been
extensively validated
for a wide range of flows
• rotating homogeneous shear flows,
• free flows
• jets and mixing layers,
• channel and boundary layer flows, and
• separated flows.

34. • For all these cases, the performance of the
model has been found to be substantially
better than that of the standard k- model.
Especially noteworthy is the fact that the
realizable k- model resolves the round-jet
anomaly; i.e., it predicts the spreading rate
for axisymmetric jets as well as that for
planar jets.

35. Effects of Buoyancy on Turbulence in
the k- Models
• When a nonzero gravity field and
temperature gradient are present

37. • It can be seen from the transport equations
for k that
turbulent kinetic energy tends to be
augmented (Gb > 0) in unstable
stratification.

38. • For stable stratification, buoyancy tends to
suppress the turbulence (Gb < 0).

39. • The effects of buoyancy on the generation
of k are always included when you have both a
nonzero gravity field and a nonzero
temperature (or density) gradient.
• While the buoyancy effects on the
generation of k are relatively well
understood, the effect on is less clear.

41. • v is the component of the flow
velocity parallel to the gravitational vector
and
u is the component of the flow velocity
perpendicular to the gravitational vector.
• In this way, will become 1 for buoyant shear
layers for which the main flow direction is
aligned with the direction of gravity.
• For buoyant shear layers that are
perpendicular to the gravitational vector,
will become zero.