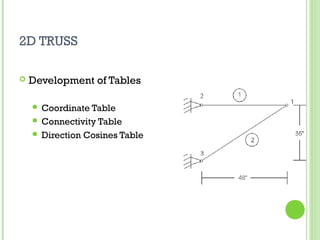
The document provides an overview of the finite element method (FEM), detailing its historical development and applications in solving partial differential equations through numerical methods. It discusses the evolution of FEM from early predictions of natural frequency to the integration of FEM with computer-aided design (CAD) in product design processes. Key concepts, one-dimensional rod elements, and two-dimensional trusses are also explained, highlighting methods of analysis such as Rayleigh-Ritz and Galerkin's method.











![1D ROD ELEMENTS Element -1 Element-2
1 T e
Element strain energy U e = q [k ]q
2
Element stiffness matrix
E e Ae 1 − 1
[k ] =
e
− 1 1
le
Load vectors
Element body load vector
Element traction-force vector e Ae l e f 1
f =
2 1
e Tl e 1
T =
2 1](https://image.slidesharecdn.com/femppt-130313204553-phpapp01/85/Introduction-to-finite-element-method-fem-12-320.jpg)

![2D TRUSS
Transformation Matrix
Direction Cosines
le = ( x2 − x1 ) 2 + ( y 2 − y1 ) 2
x 2 − x1
l m 0 0 l = cos θ =
[ L] = le
0 0 l m
y 2 − y1
m = sin θ =
le](https://image.slidesharecdn.com/femppt-130313204553-phpapp01/85/Introduction-to-finite-element-method-fem-14-320.jpg)
![2D TRUSS
Element Stiffness Matrix
l2 lm − l 2 − lm
2
E e Ae lm m2 − lm − m
[k e ] =
l e − l 2 − lm l2 lm
2
− lm − m
2
lm m ](https://image.slidesharecdn.com/femppt-130313204553-phpapp01/85/Introduction-to-finite-element-method-fem-15-320.jpg)



![2D TRUSS
Element Stresses
Ee
σ= [ − l − m l m] q
le
Element Reaction Forces
R = [ K ]Q](https://image.slidesharecdn.com/femppt-130313204553-phpapp01/85/Introduction-to-finite-element-method-fem-19-320.jpg)



![3D TRUSS STIFFNESS MATRIX
3D Transformation Matrix
Direction Cosines
l m n 0 0 0
[ L] =
0 0 0 l m n
le = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 + ( z 2 − z1 ) 2
x 2 − x1 y 2 − y1 z 2 − z1
l = cos θ = m = cos φ = n = cos ϕ =
le le le](https://image.slidesharecdn.com/femppt-130313204553-phpapp01/85/Introduction-to-finite-element-method-fem-24-320.jpg)
![3D TRUSS STIFFNESS MATRIX
3D Stiffness Matrix
l2 lm ln − l 2 − lm − ln
lm m2 mn − lm − m 2 − mn
E e Ae ln mn n2 − ln − mn − n 2
[k e ] =
l e − l 2 − lm − ln l 2
lm ln
− lm − m 2 − mn lm m2 mn
− ln − mn − n
2 2
ln mn n ](https://image.slidesharecdn.com/femppt-130313204553-phpapp01/85/Introduction-to-finite-element-method-fem-25-320.jpg)












