Downloaded 2,460 times
Uploaded byDr Renju Ravi
P value
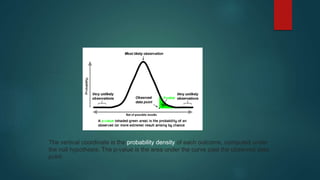
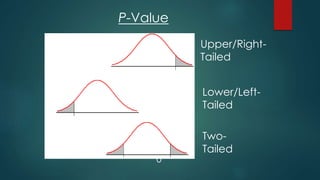
This document discusses p-values and their significance in statistical hypothesis testing. It defines a p-value as the probability of obtaining a result equal to or more extreme than what was observed assuming the null hypothesis is true. Lower p-values indicate stronger evidence against the null hypothesis. The document outlines the steps in hypothesis testing which include stating hypotheses, determining acceptable type I and type II error rates, selecting a statistical test to calculate a test statistic, determining the p-value, making inferences, and forming conclusions. It emphasizes that statistical significance does not necessarily imply real-world significance.
More Related Content
P value
- 1. P value andits significance DR.RENJU.S.RAVI 1
- 2. INTRODUCTION Statisticsinvolves collecting, organizing and interpreting the data Descriptive statistics : Describe what is there in our data. Inferential statistics : Make inferences from our data to more general conditions.
- 3. Inferential statistics Data taken from a sample is used to estimate a population parameter. Explain the relationship between the observed state of affairs to a hypothetical true state of affairs. Hypothesis testing (P-values) Point estimation (Confidence intervals)
- 4. Definition p-value isdefined as the probability of obtaining a result equal to or more extreme than what was actually observed. The p-value was first introduced by Karl Pearson in his Pearson's chi-squared test . The smaller the p-value, the larger the significance because it tells the investigator that the hypothesis under consideration may not adequately explain the observation.
- 5. The vertical coordinateis the probability density of each outcome, computed under the null hypothesis. The p-value is the area under the curve past the observed data point.
- 6. steps in significancetesting Stating the research question Determine probability of erroneous conclusions Choice of statistical test / to calculate test statistic Getting the ‘p’ value Inference Forming conclusions
- 7. Stating Research Question Research question. Idea is to assume the state of affairs in the two treatment populations. Eg: Is mean Hb in urban and rural children the same?
- 8. Null and AlternateHypothesis Ho(Null Hypothesis): Assumes that the two population being compared are not different. HA/H1 (Alternative Hypothesis): Assumes that the two groups are different. Two competing Hypothesis are not treated on an equal basis Special consideration is given to the null hypothesis. We test the null hypothesis and if there is enough evidence to say that the null hypothesis is wrong ,we reject the null hypothesis in favour of the alternative hypothesis. Rejecting null hypothesis suggests that the alternative hypothesis may be true.
- 9. Determine probability oferroneous conclusions Truth H0(no difference) H1(difference exists) Decision Accept H0 Right Decision Type II Error Reject H0 Type I Error Right Decision
- 10. Type I error/False positive conclusion stating difference when there is no difference Probability (Type I Error) = Usually set at 1/20 or 0.05. never 0 and it should be below the value of ‘α’ for concluding statistical significance. The probability of a type I error is distributed at the tails of the normal curve i.e. 0.025 on either tail.
- 11. Type II Error/false negative conclusion Stating no difference when actually there is i.e. missing a true difference Occurs when sample size is too small. Probability (Type II Error) = Conventionally accepted to be 0.1 – 0.2 Power of a study =(1- ) Researchers consider a power 0.8 – 0.9 (80- 90%) as satisfactory.
- 12. Cut off forp value Arbitrary cut-off 0.05 (5% chance of a false +ve conclusion. If p<0.05 statistically significant- Reject H0, Accept H1 If p>0.05 statistically not-significant- Accept H0, Reject H1 Testing potential harmful interventions ‘α’ value is set below 0.05
- 13. Low p value • If p is very small (<0.001), then the null hypothesis appears not realistic because the difference could hardly ever arise due to chance, when the null hypothesis is true.
- 14. Test Statistic •In order to arrive at the p value we need to compute the test statistic which is Observed Hypothesized SE(Observed)
- 15. Step 4. Gettingthe ‘p’ value Each test statistic has a sampling distribution from which ‘p’ values for the corresponding value of the ‘statistic’ can be noted from available tables.
- 16. Step 5. Inference If the obtained ‘p’ value is smaller than the level of ‘α’ - statistically significant , null hypothesis is rejected ‘p’ value more than the level of ‘α’ – not significant, null hypothesis cannot be rejected
- 17. Step 6. Conclusion If the results are statistically significant, decide whether the observed differences are clinically important. If not significant, see if the sample size was adequate enough not to have missed a clinically important difference ‘The power of the study ‘ tells us the strength which we can conclude that there is no difference between the two groups.
- 18. Statistical significancedoes not necessarily mean real significance • If sample size is large, even very small differences can have a low p-value. • Lack of significance does not necessarily mean that the null hypothesis is true. • If sample size is small, there could be a real difference, but we are not able to detect it
- 19. One/Two sided pvalues If we are interested only to find out whether the test drug is better than the control drug, we put the α of 0.05 under only one tail of hypothesis - called one tailed test. To know whether one drug performs better or worse than the other, we would distribute the of 0.05 to both tails under the hypothesis i.e. 0.025 to each tail – two tailed test.
- 20. P-Value 0 0 0 Upper/Right- Tailed Lower/Left- Tailed Two- Tailed
- 21. ‘p’ value- Pointsto remember… The P-value is the smallest level of significance at which H0 would be rejected when a specified test procedure is used on a given data set. 0.05 is arbitrary cut off value Type 1 error (α)- false positive conclusion Type 2 error (β)- false negative conclusion
- 22.