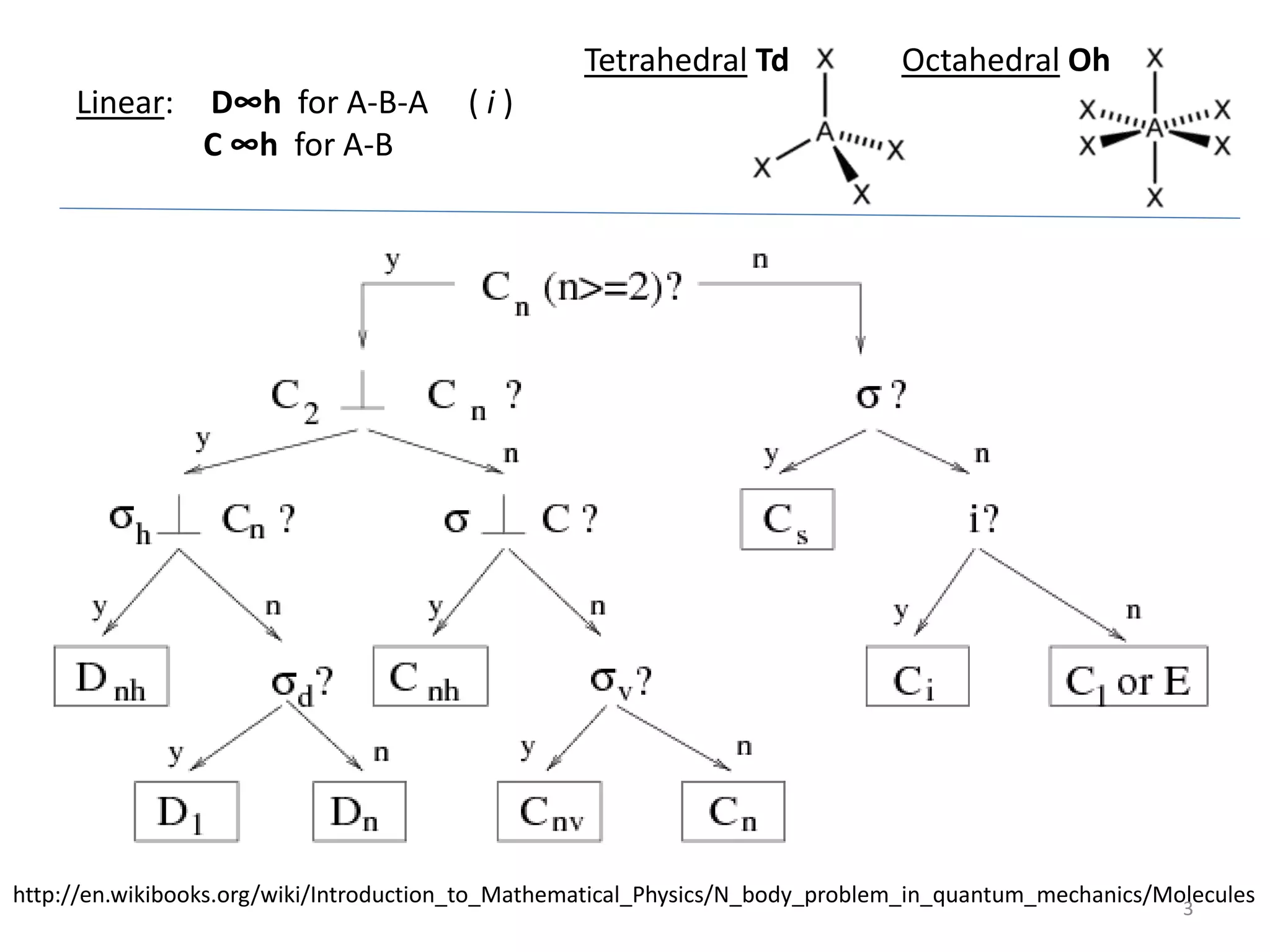
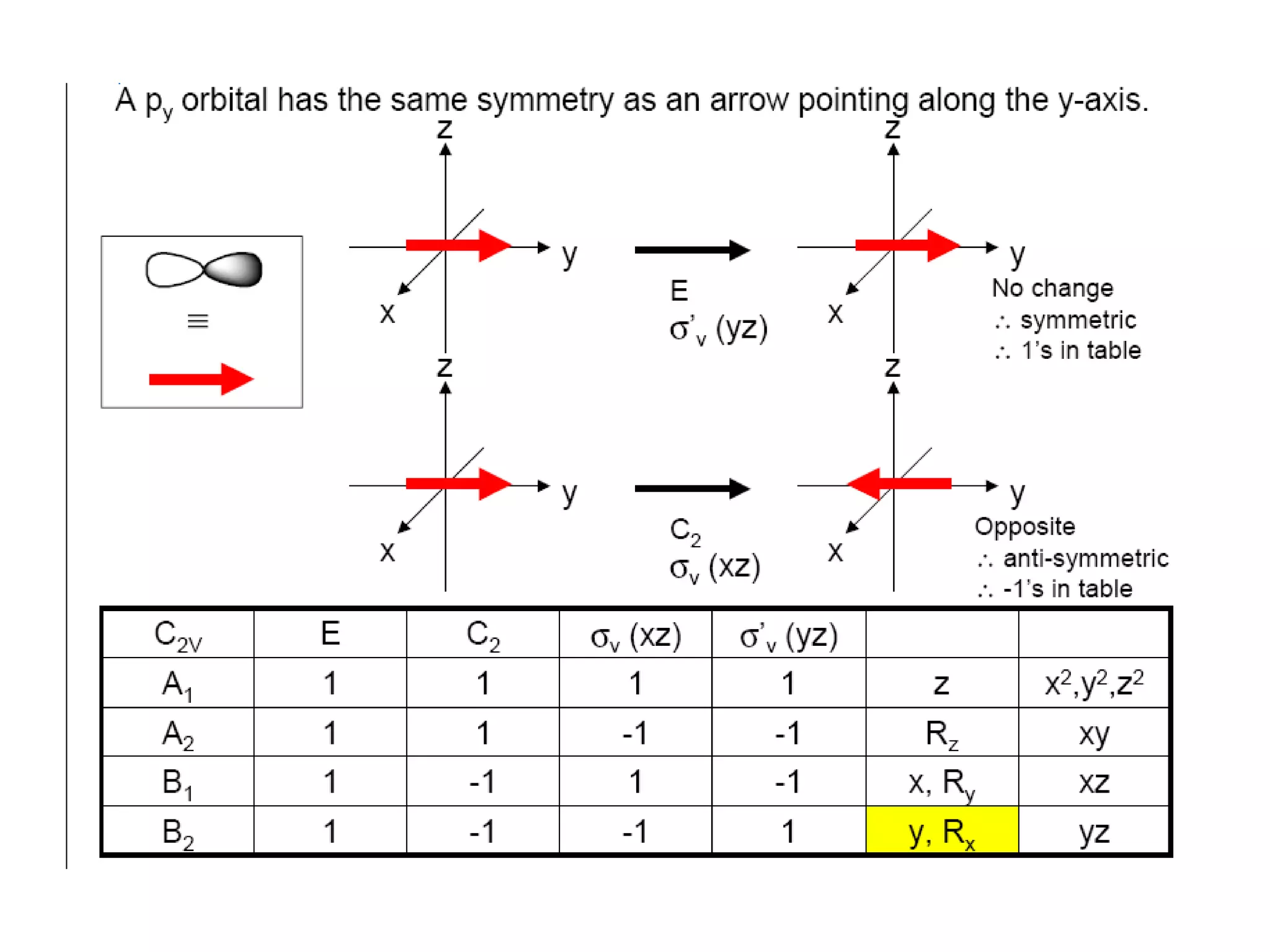
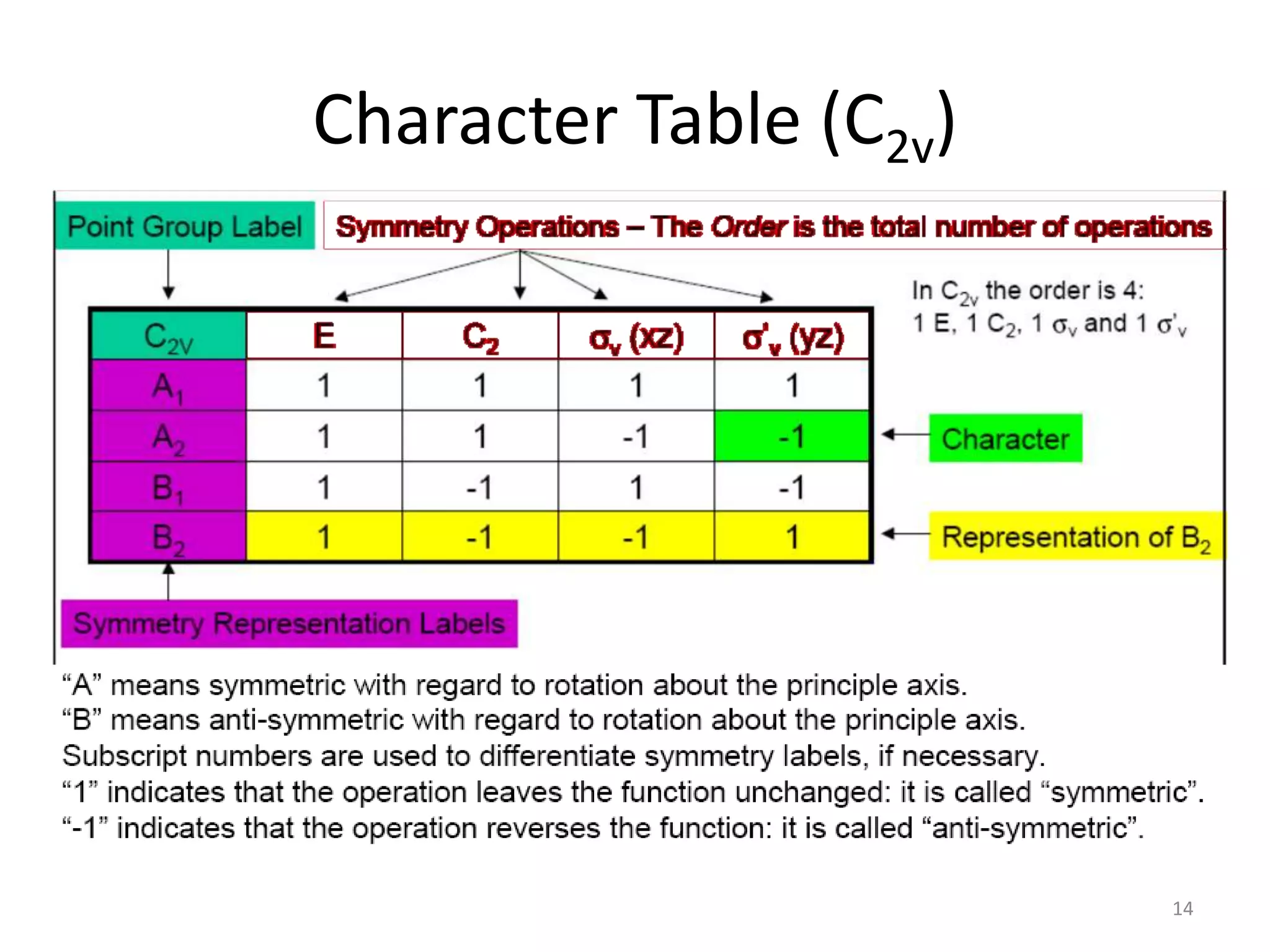
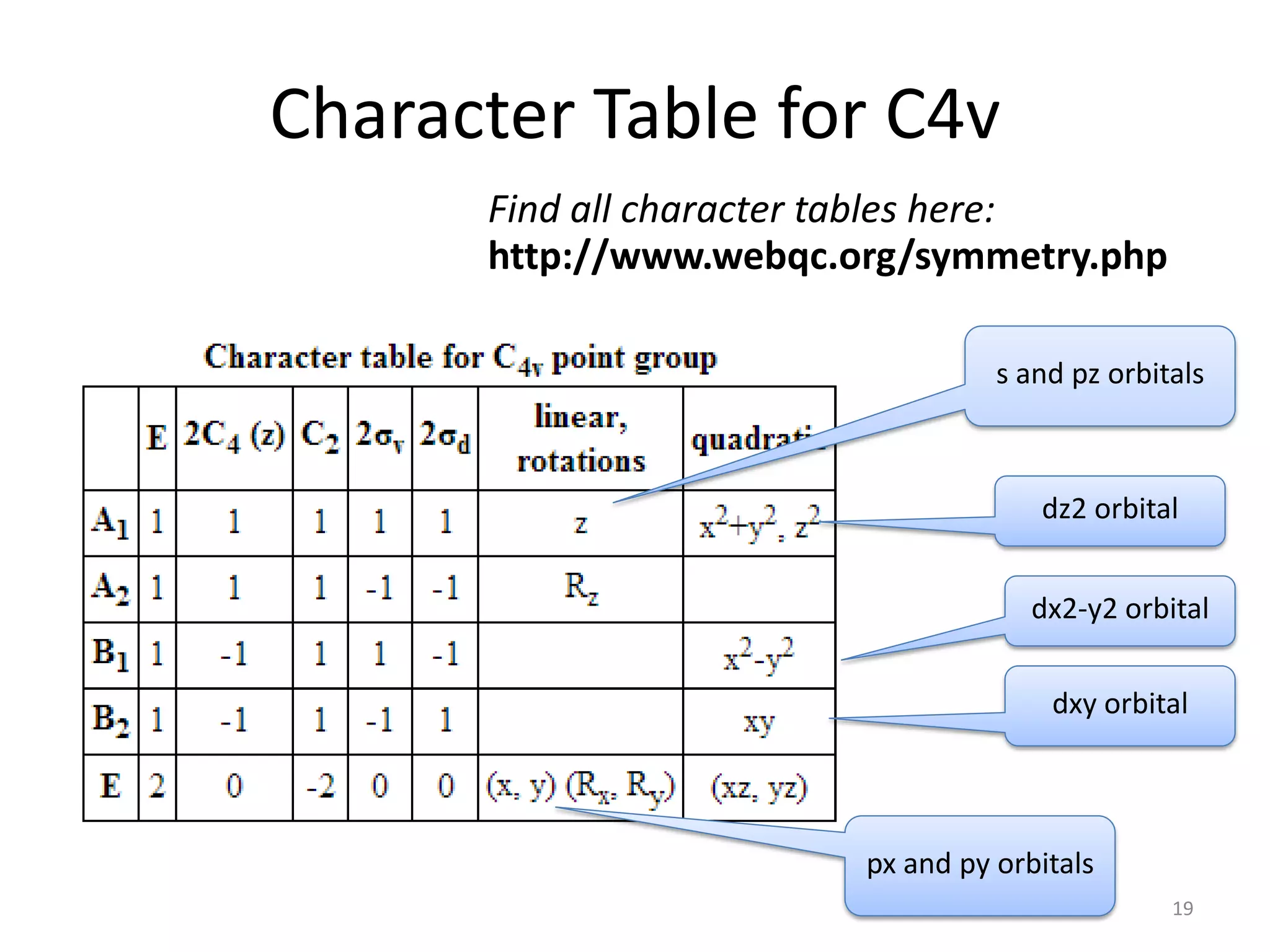
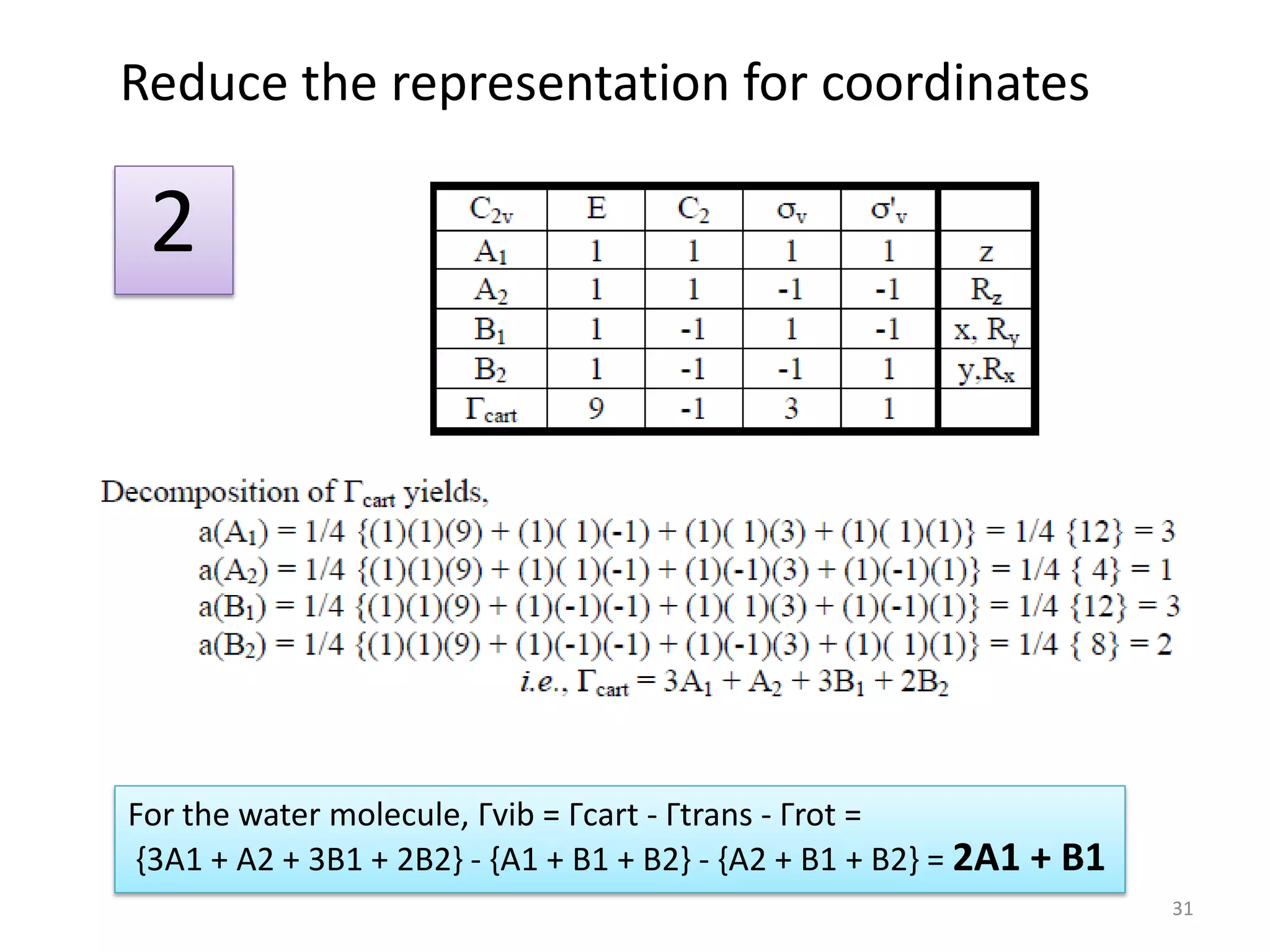
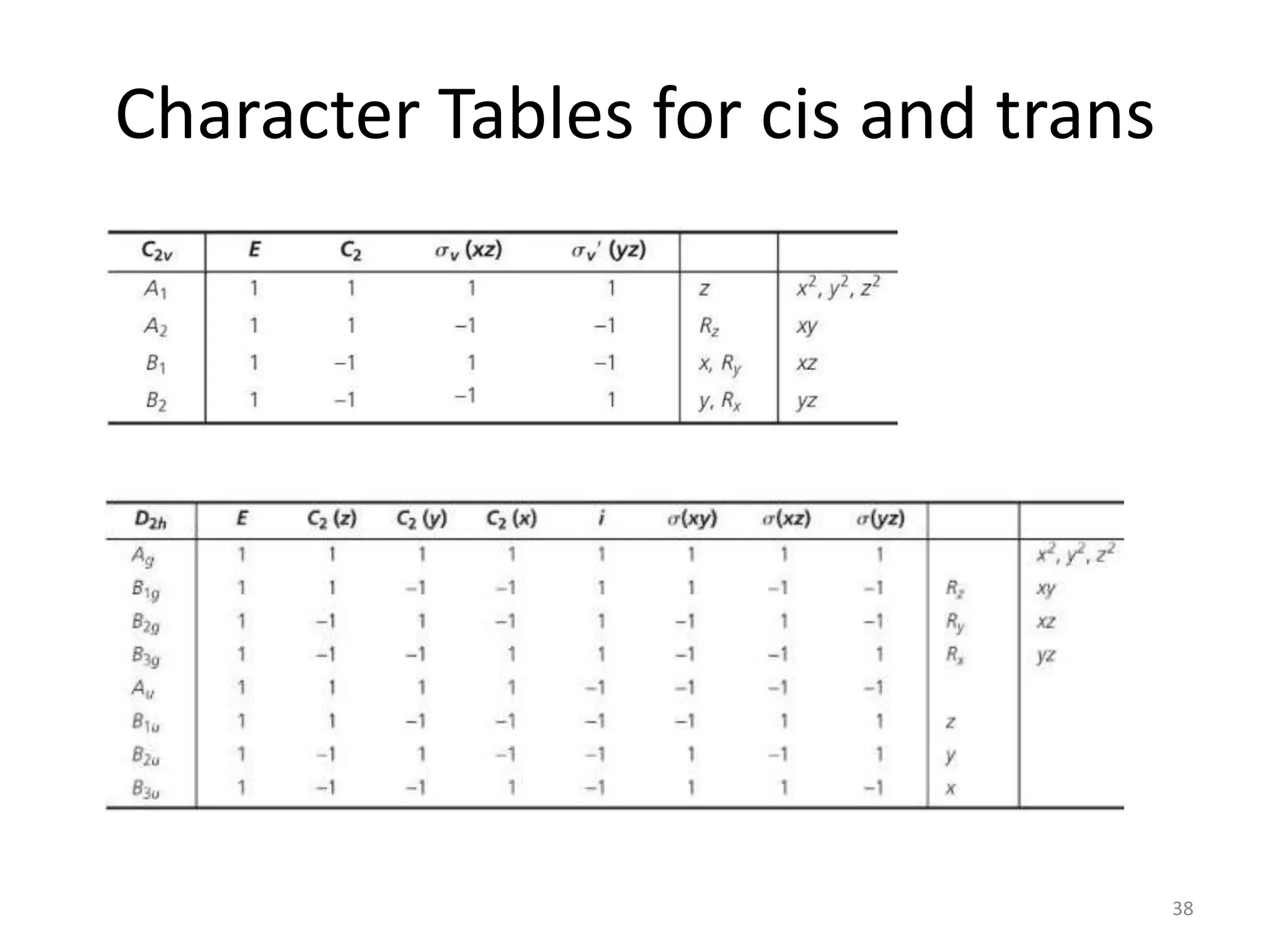
The document covers the fundamentals of symmetry operations, point groups, and representations in molecular properties such as vibrations and orbitals. It explains how to determine character tables for specific molecules and the significance of irreducible representations in understanding molecular behavior under these symmetry operations. Additionally, it discusses applications of group theory in predicting molecular vibrations and hybridization in various chemical contexts.






















![“Reduction” Formula – if we cannot see by just testing:
# A1 = (1/4) * [ (2 * 1 *1) + (0) + (2 * 1 *1) + (0) ] = 1
=> Γ contains 1x A1
# B1 = (1/4) * [ (2 *1 *1) + (0) + (2 *1 *1) ] = 1
=> Γ contains 1x B1
27
Г = 2 0 2 0
h = 4](https://image.slidesharecdn.com/charactertables2013-140626102835-phpapp01/75/Character-tables-27-2048.jpg)


















![“Reduction” of Гred
# A1’ = 1/12 *
[ ( 3 * 1 * 1) + ( 0) + (1 * 1 * 3) +
( 3 * 1 * 1) + (0) + ( 1 *1 *3)] = 1
Try the same method for A2’ and E’ !
48](https://image.slidesharecdn.com/charactertables2013-140626102835-phpapp01/75/Character-tables-48-2048.jpg)
![“Reduction”
This is a reducible representation, so use character table to reduce it.
D3h E 2C3 3C2 σh 2S3 3σv
Г 3 0 1 3 0 1
#A1’ = (1/12) [ 3 + 0 + 3 + 3 + 0 + 3] = 1
#A2’ = (1/12) [ 3 + 0 - 3 + 3 + 0 - 3] = 0
…
#E’ = (1/12) [ 6 + 0 + 0 + 6 + 0 + 0] = 1
Г = A1’ + E’
Which orbitals belong to these symmetry species?
A1’ = s-orbital
E’ = 2 p-orbitals
Therefore, it is an sp2 hybrid orbital 49](https://image.slidesharecdn.com/charactertables2013-140626102835-phpapp01/75/Character-tables-49-2048.jpg)







![Reducing Г
57
# A1 = ¼ [ (3) + (1) + (3) + (1) ] = 2
# B1 = ¼ [ (3) + (-1) + (3) + (-1) ] = 1](https://image.slidesharecdn.com/charactertables2013-140626102835-phpapp01/75/Character-tables-57-2048.jpg)
