More Related Content
PDF
PDF
PDF
Tech-Circle #18 Pythonではじめる強化学習 OpenAI Gym 体験ハンズオン PDF
PPTX
最新の多様な深層強化学習モデルとその応用(第40回強化学習アーキテクチャ講演資料) PPTX
PILCO - 第一回高橋研究室モデルベース強化学習勉強会 PDF
[DL輪読会]近年のオフライン強化学習のまとめ —Offline Reinforcement Learning: Tutorial, Review, an... PPTX
What's hot
PPTX
[DL輪読会]Set Transformer: A Framework for Attention-based Permutation-Invariant... PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning PDF
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PPTX
近年のHierarchical Vision Transformer PPTX
【DL輪読会】ViT + Self Supervised Learningまとめ PDF
PPTX
PDF
PDF
最近のディープラーニングのトレンド紹介_20200925 PPTX
PDF
PDF
PDF
Viewers also liked
PDF
PDF
PDF
Humor Recognition and Humor Anchor Extraction PDF
Learning Better Embeddings for Rare Words Using Distributional Representations PPTX
PDF
[Yang, Downey and Boyd-Graber 2015] Efficient Methods for Incorporating Knowl... PPTX
PPTX
強化学習を利用した自律型GameAIの取り組み ~高速自動プレイによるステージ設計支援~ #denatechcon PDF
Memory Networks (End-to-End Memory Networks の Chainer 実装) PDF
無限関係モデル (続・わかりやすいパターン認識 13章) PDF
PDF
PDF
A Neural Attention Model for Sentence Summarization [Rush+2015] PDF
PPTX
PDF
Similar to 強化学習その1
PDF
PDF
PDF
PDF
PPTX
強化学習の基礎と深層強化学習(東京大学 松尾研究室 深層強化学習サマースクール講義資料) PDF
PDF
PPTX
PPTX
PPTX
Machine Learning Seminar (1) PDF
PPTX
PDF
オンライン凸最適化と線形識別モデル学習の最前線_IBIS2011 PDF
PDF
PDF
Top-K Off-Policy Correction for a REINFORCE Recommender System PDF
PDF
PDF
PPTX
Reinforcement Learning(方策改善定理) More from nishio
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
首都大学東京「情報通信特別講義」2016年西尾担当分 PPTX
PDF
PDF
PDF
PDF
Wifiにつながるデバイス(ESP8266EX, ESP-WROOM-02, ESPr Developerなど) PDF
PDF
「ネットワークを作ることで�イノベーションを加速」�ってどういうこと? PDF
強化学習その1
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
UCB1
UCB1ではまず 𝑡 =2
log 𝑇
𝑛
と決め打ちする。Tは
全試行数。これを右辺に代入すると
𝑃 ത𝑋 − 𝜇 > 𝑡 ≤ exp −2𝑛𝑡2
= 𝑇−4
となる。少し変形すると
𝑃 ത𝑋 − 𝑡 < 𝜇 < ത𝑋 + 𝑡 ≤ 1 − 2𝑇−4
となり、 ത𝑋 + 𝑡はT増加とともにだんだん広くなる
信頼区間の上の端ということになる。
44
https://en.wikipedia.org/wiki/Hoeffding's_inequality
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
sumが3重になる
𝑁 𝑇,𝑖 ≤𝑚 +
𝑡=𝐾+1
𝑇
𝜒 𝐼𝑡 = 𝑖 かつ 𝑁𝑡−1,𝑖 ≥ 𝑚
≤ 𝑚 +
𝑡=𝐾+1
𝑇
𝑠=𝑚
𝑡−1
𝑠′=1
𝑡−1
𝜒
ҧ𝑥𝑖,𝑠 + 𝑎 𝑠, 𝑡 − 1
> ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡 − 1
かつ 𝑁𝑡−1,𝑖 ≥ 𝑚
51
「ある値ペアs, s’で1」の時「すべての値ペアs, s’で和を取ったもの」は1以上なので。
- 52.
- 53.
iを選ぶ確率の計算
∗ ҧ𝑥𝑖,𝑠 +𝑎 𝑠, 𝑡 > ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
の起こる確率を計算する。3つの可能性がある。
1 𝜇1 ≥ ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
2 𝜇𝑖 ≤ ҧ𝑥𝑖,𝑠 − 𝑎 𝑠, 𝑡
3 𝜇1 − 𝜇𝑖 < 2𝑎(𝑠, 𝑡)
(1)(2)がFalseなら(3)がTrueになることが示せるの
で(*)の起こる確率はこの3つの和以下である。
53
- 54.
(1)(2)がFalseなら(3)がTrueになる
∗ ҧ𝑥𝑖,𝑠 +𝑎 𝑠, 𝑡 > ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
1 𝜇1 ≥ ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
2 𝜇𝑖 ≤ ҧ𝑥𝑖,𝑠 − 𝑎 𝑠, 𝑡
3 𝜇1 − 𝜇𝑖 < 2𝑎(𝑠, 𝑡)
(1)(2)がFalseなので(*)を使って以下が言える
𝜇1 < ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡 < ҧ𝑥𝑖,𝑠 + 𝑎 𝑠, 𝑡
ҧ𝑥𝑖,𝑠 − 𝑎 𝑠, 𝑡 < 𝜇𝑖
前提として𝜇1 ≥ 𝜇𝑖なので(3)が言える
54
- 55.
iを選ぶ確率の計算
(*)の起こる確率はこの3つの和以下
1 𝜇1 ≥ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
2 𝜇𝑖 ≤ ҧ𝑥𝑖,𝑠 − 𝑎 𝑠, 𝑡
3 𝜇1 − 𝜇𝑖 < 2𝑎(𝑠, 𝑡)
(1)(2)は「信頼区間の外」なので𝑇−4
となる。
(3)の計算で「かつ 𝑁𝑡,𝑖 ≥ 𝑚 」の条件を使う。
mが十分大きければ確率が0になることを示す。
(mを導入したのはこのためだ!)
55
- 56.
𝜇1 − 𝜇𝑖< 2𝑎(𝑠, 𝑡)の確率を求める
再掲: 𝑎 𝑛, 𝑇 = 2log 𝑇/𝑛
もし m ≥
8 log 𝑇
𝜇1−𝜇 𝑖
2 なら s ≥ m なので
2𝑎 𝑠 , 𝑡 = 2 2log 𝑡/𝑠 ≤ 2
2log 𝑡
8 log 𝑇
𝜇1 − 𝜇𝑖
2
= 𝜇1 − 𝜇𝑖
log 𝑡
log T
≤ 𝜇1 − 𝜇𝑖
よってmが上記条件の時、確率は0になる。
56
- 57.
- 58.
Nの期待値を求める
𝐸[𝑁 𝑇,𝑖] ≤𝑚 +
𝑡=1
∞
𝑠=𝑚
𝑡−1
𝑠′=1
𝑡−1
𝑃
ҧ𝑥𝑖,𝑠 + 𝑎 𝑠, 𝑡
> ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
かつ 𝑁𝑡,𝑖 ≥ 𝑚
≤ 𝑚 +
𝑡=1
∞
𝑠=𝑚
𝑡−1
𝑠′=1
𝑡−1
2𝑡−4
≤ 𝑚 + 2
𝑡=1
∞
𝑡−2
≤
8 log 𝑇
𝜇1 − 𝜇𝑖
2
+ 1 +
𝜋2
3
つまりO(log T)である。
58
Basel Problem
𝑛=1
∞
1
𝑛2
=
𝜋2
6
- 59.





















![どうしてこうなる?
スロット2は当たり率0.3, 期待値150だけど、
3回の試行でたまたま[0, 0, 0]となることは
0.7 * 0.7 * 0.7 = 0.343 の確率で起きて
「このスロットの期待値は0だな」
と悲観的な勘違いをする。
これ以外にも色々な悲観的勘違いが起きる。
一度悲観的な勘違いをすると、
二度とそのスロットを試さないので
勘違いから脱出できない。
22
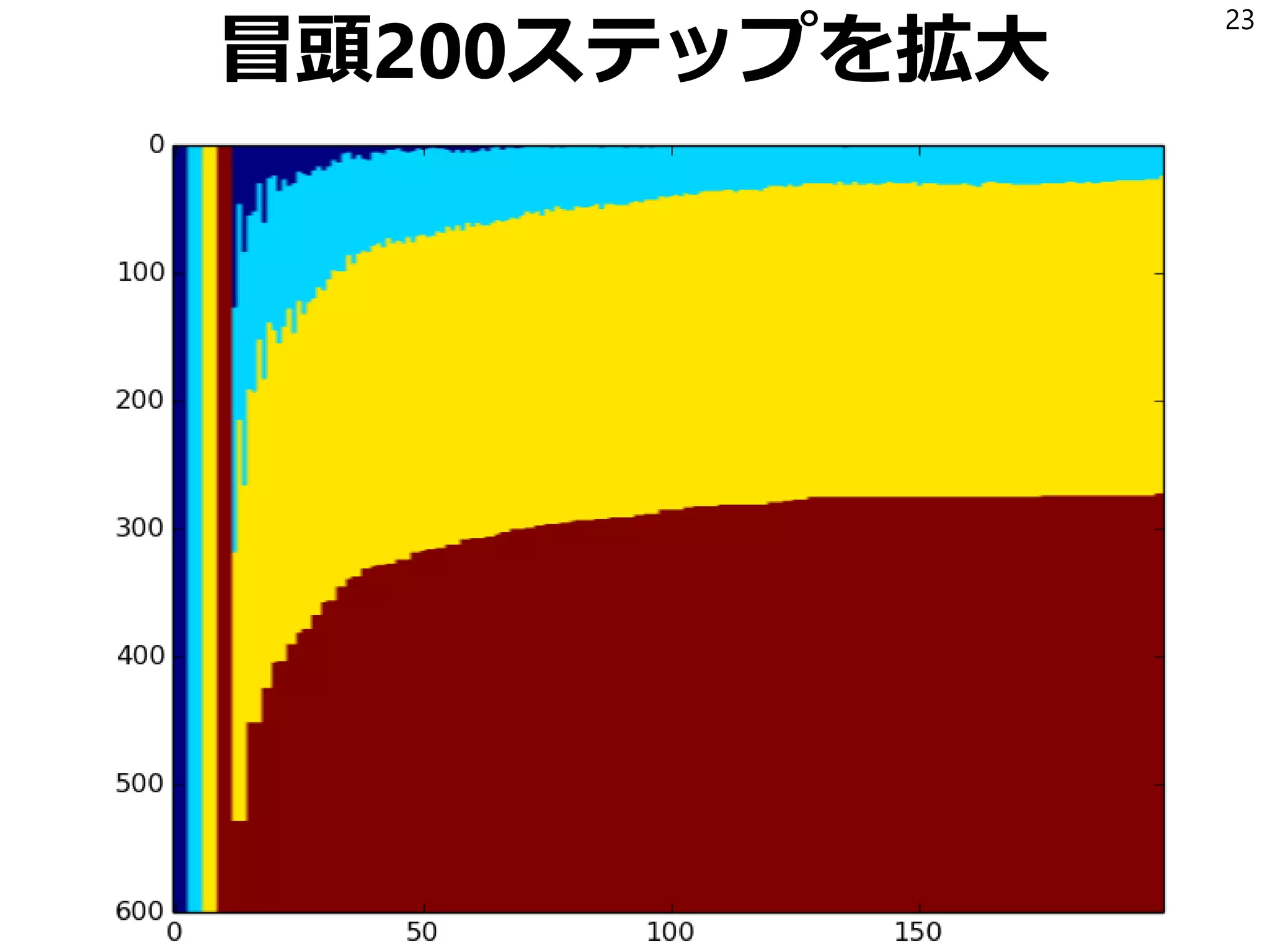
昔ペン入力のPCを買ってイマイチだったからそれ以来買ってないけど悲観的勘違いかも](https://image.slidesharecdn.com/1-170113055708/75/1-22-2048.jpg)


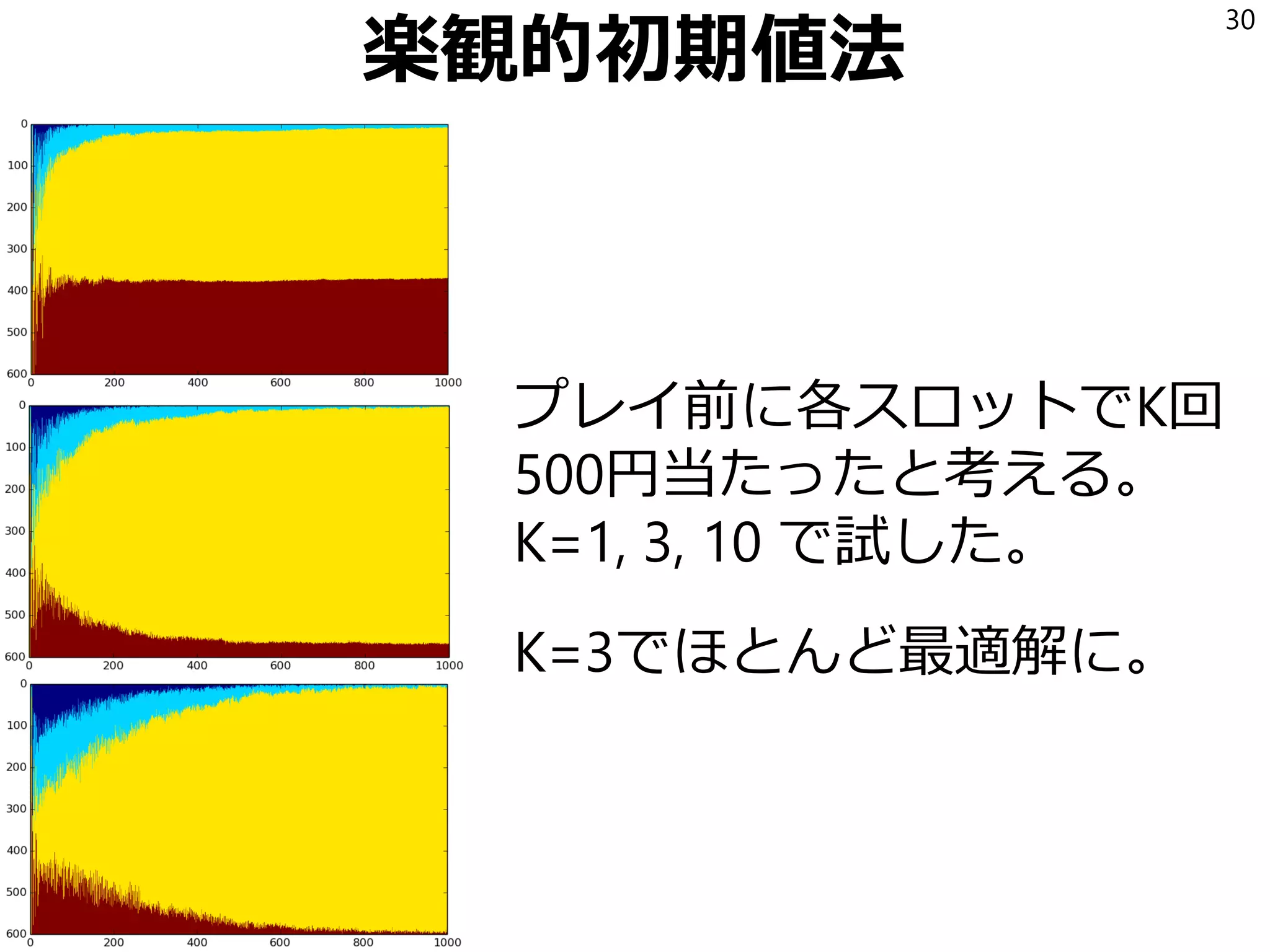
![不確かなときは楽観的に
この考え方には名前がついている。
「不確かなときは楽観的に」の原理
(optimism in face of uncertainty)
探索と利用のトレードオフを解く
アルゴリズムの多くが
この原理に従っている。
26
座右の銘として飾っておいてもよさそう。強化学習は人生。
[Bubeck and Cesa-Bianchi: 2012] https://arxiv.org/pdf/1204.5721.pdf](https://image.slidesharecdn.com/1-170113055708/75/1-26-2048.jpg)













![Chernoff-Hoeffding Inequality
[0, 1]の範囲の値を取る独立な確率変数
𝑋1 … 𝑋 𝑛 の平均 ത𝑋 =
1
𝑛
σ𝑖 𝑋𝑖 と真の期待値 𝜇
の差には任意の正数 𝑡 について
𝑃 ത𝑋 − 𝜇 > 𝑡 ≤ exp −2𝑛𝑡2
という関係がある。
42
https://en.wikipedia.org/wiki/Hoeffding's_inequality](https://image.slidesharecdn.com/1-170113055708/75/1-42-2048.jpg)




![リグレット
「全知の神が最善の選択肢を取り続けた場合」
と比べてどれくらい差があるかで、強化学習の
アルゴリズムの良さを評価する。
これをリグレット(Regret)という。
多腕バンディットの場合、神は期待値が最大のも
のを選び続けるので、以下の通り:
𝑅(𝑡) =
𝑖
𝜇1 − 𝜇𝑖 𝐸[𝑁 𝑡,𝑖 ]
47
t回目までにスロットiが選ばれた回数をN(t, i)、期待値最大のスロットを1とする](https://image.slidesharecdn.com/1-170113055708/75/1-47-2048.jpg)










![Nの期待値を求める
𝐸[𝑁 𝑇,𝑖] ≤ 𝑚 +
𝑡=1
∞
𝑠=𝑚
𝑡−1
𝑠′=1
𝑡−1
𝑃
ҧ𝑥𝑖,𝑠 + 𝑎 𝑠, 𝑡
> ҧ𝑥1,𝑠′ + 𝑎 𝑠′
, 𝑡
かつ 𝑁𝑡,𝑖 ≥ 𝑚
≤ 𝑚 +
𝑡=1
∞
𝑠=𝑚
𝑡−1
𝑠′=1
𝑡−1
2𝑡−4
≤ 𝑚 + 2
𝑡=1
∞
𝑡−2
≤
8 log 𝑇
𝜇1 − 𝜇𝑖
2
+ 1 +
𝜋2
3
つまりO(log T)である。
58
Basel Problem
𝑛=1
∞
1
𝑛2
=
𝜋2
6](https://image.slidesharecdn.com/1-170113055708/75/1-58-2048.jpg)
