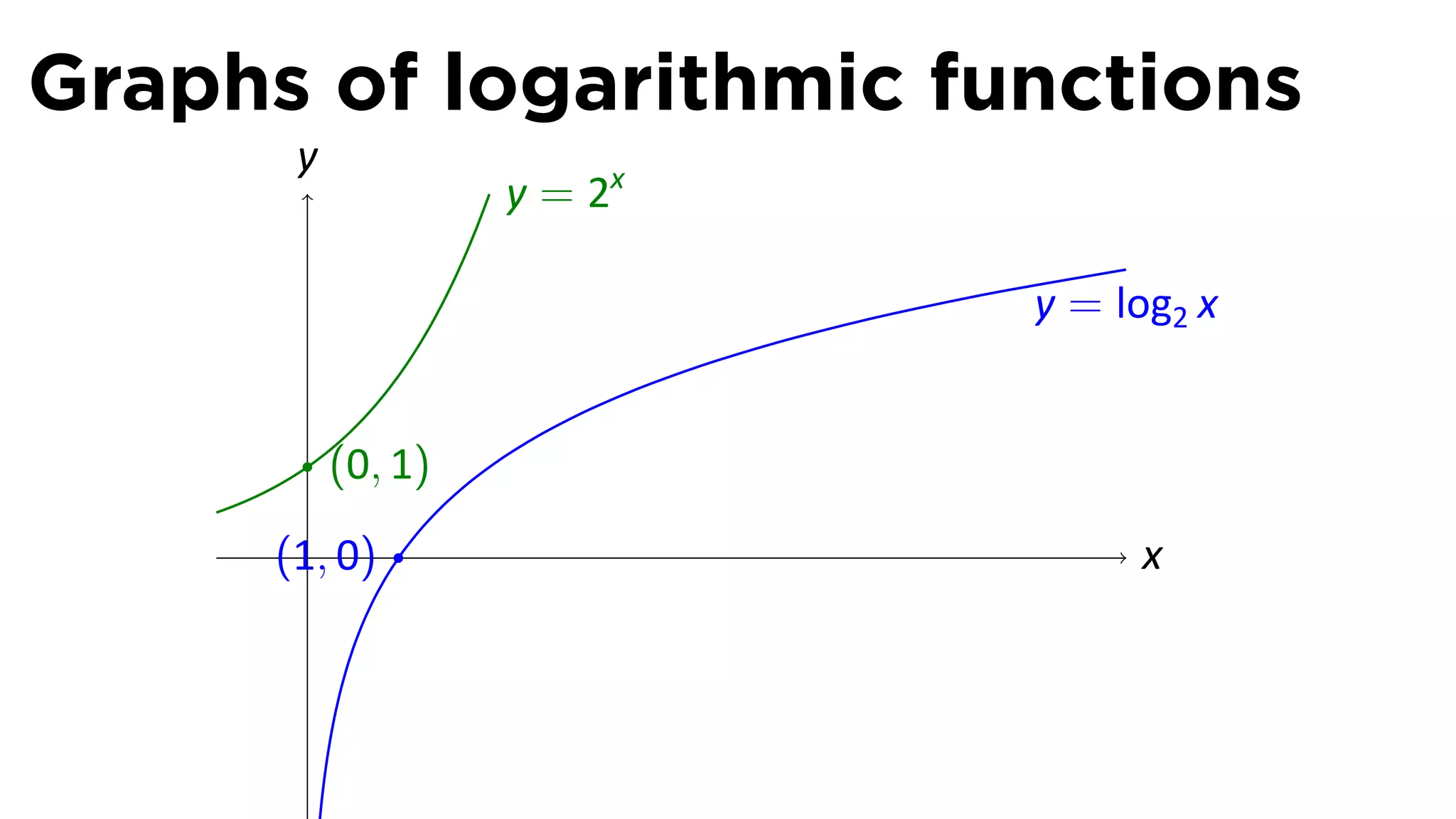
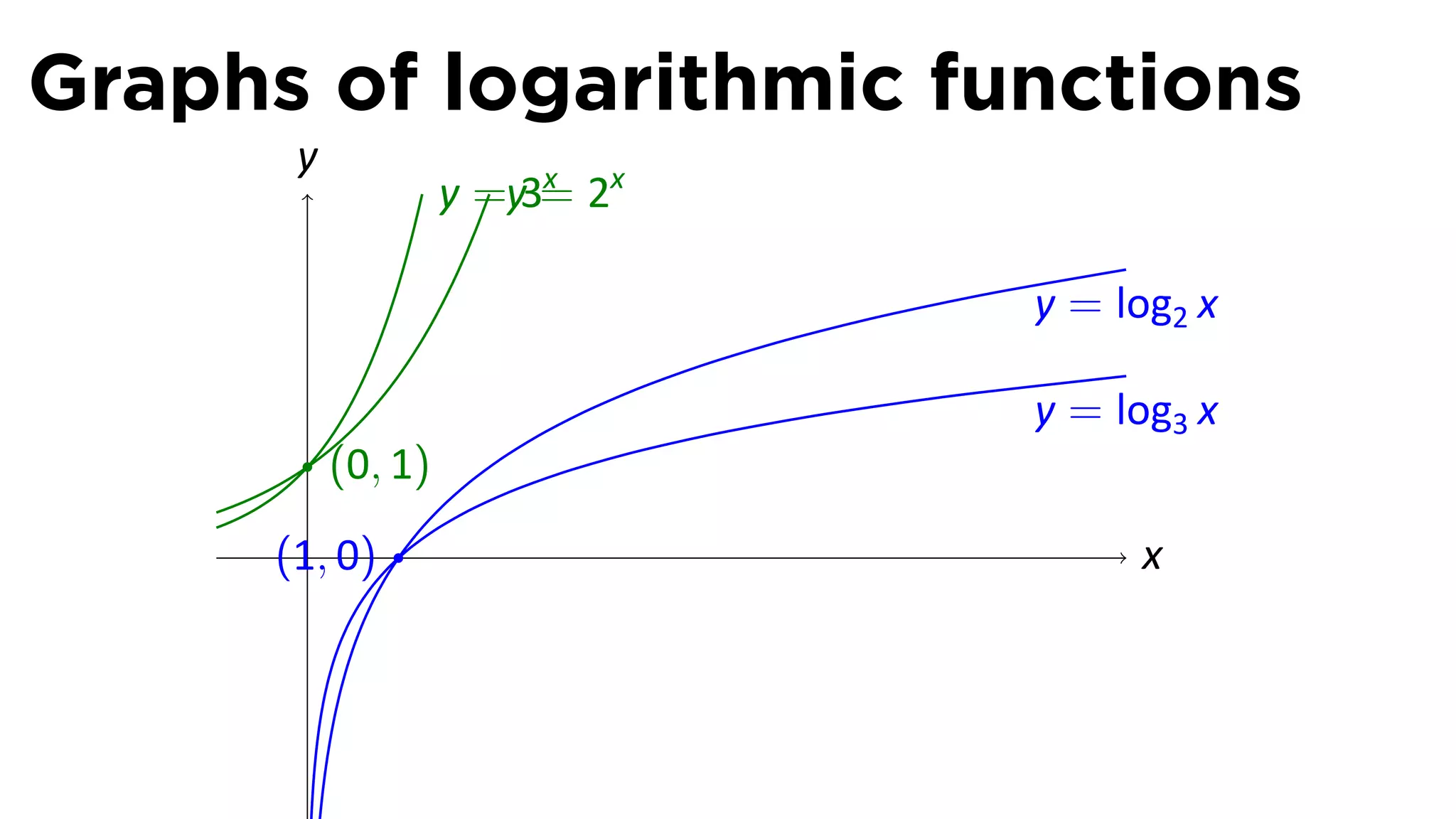
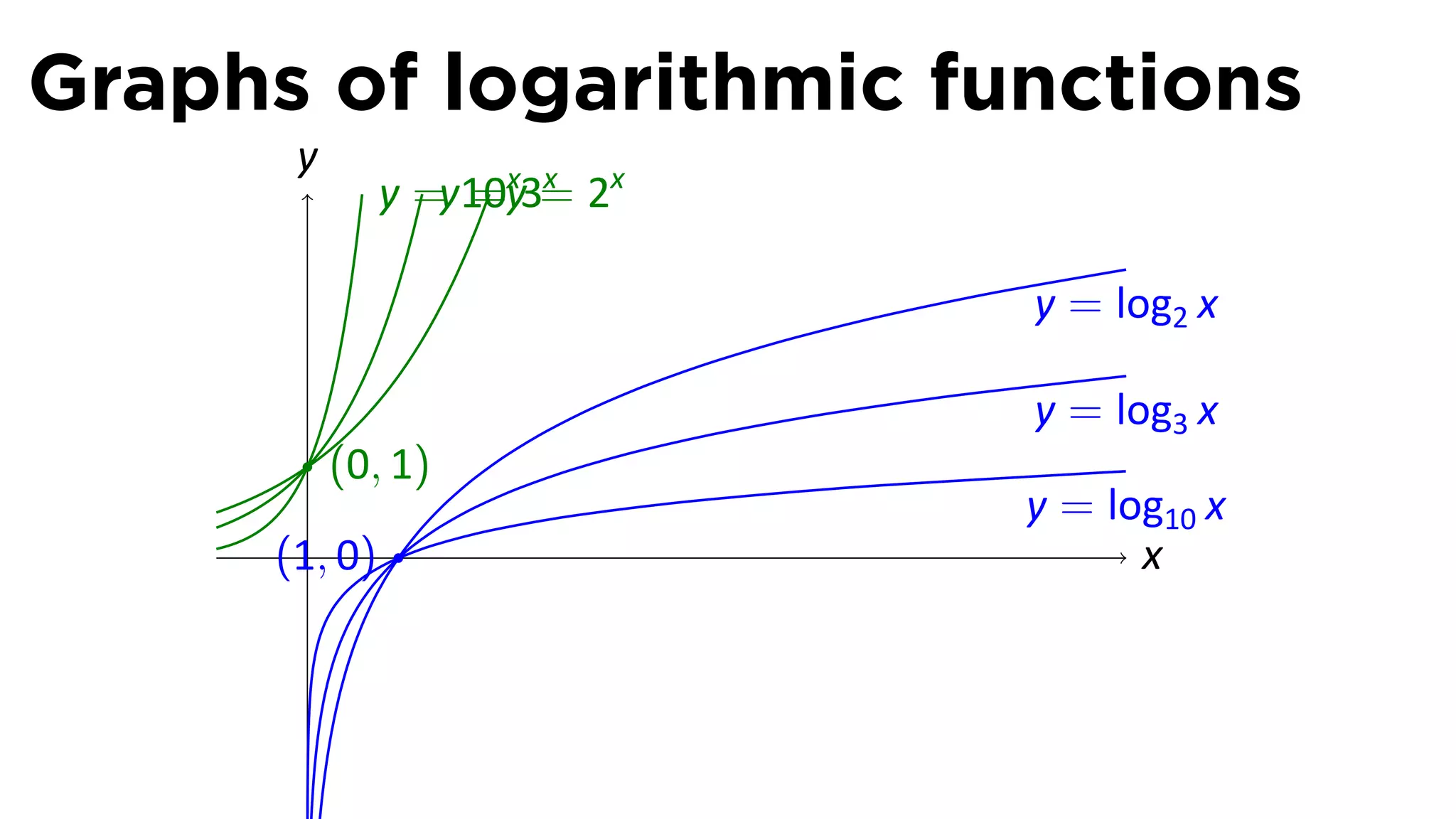
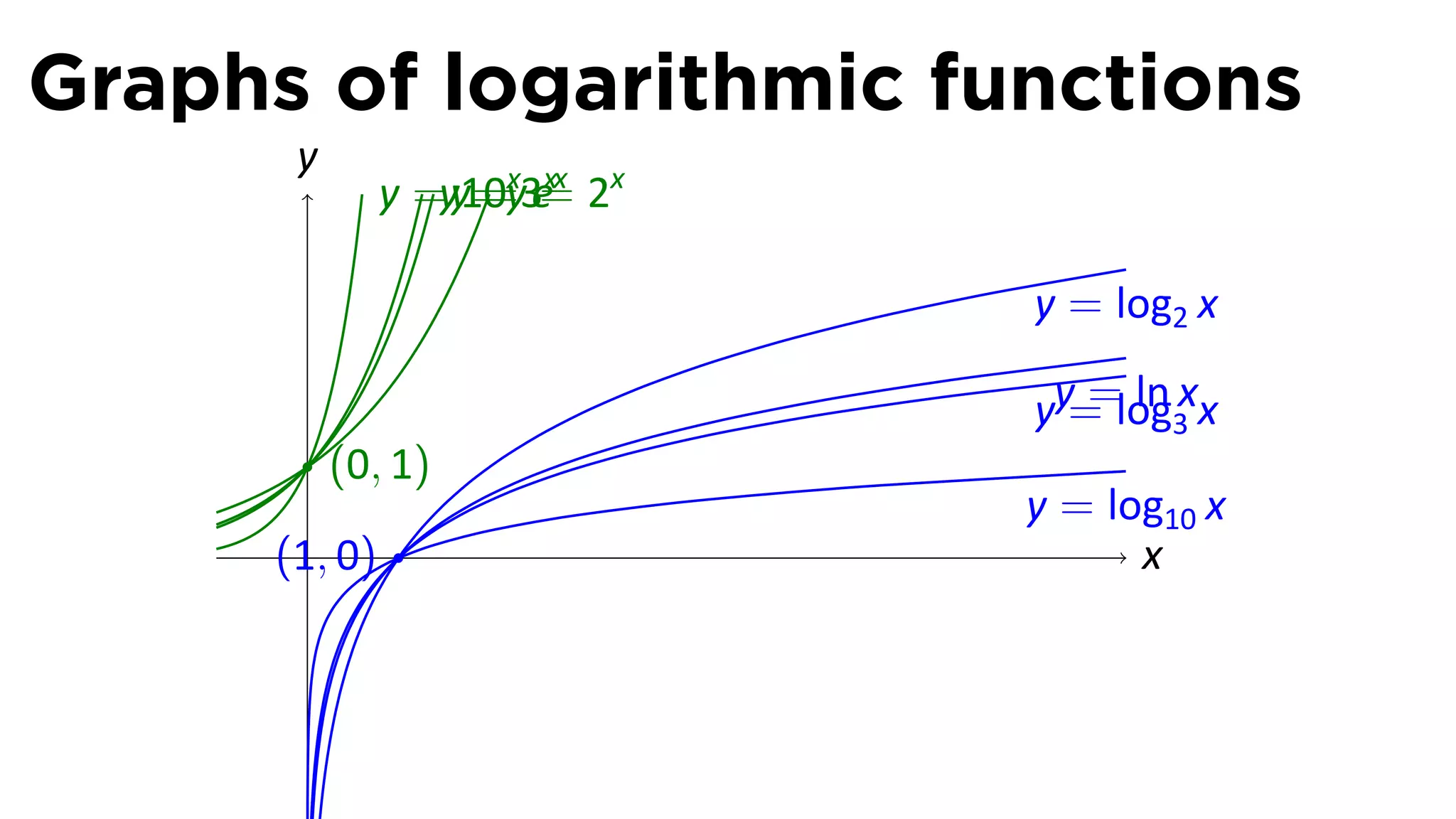
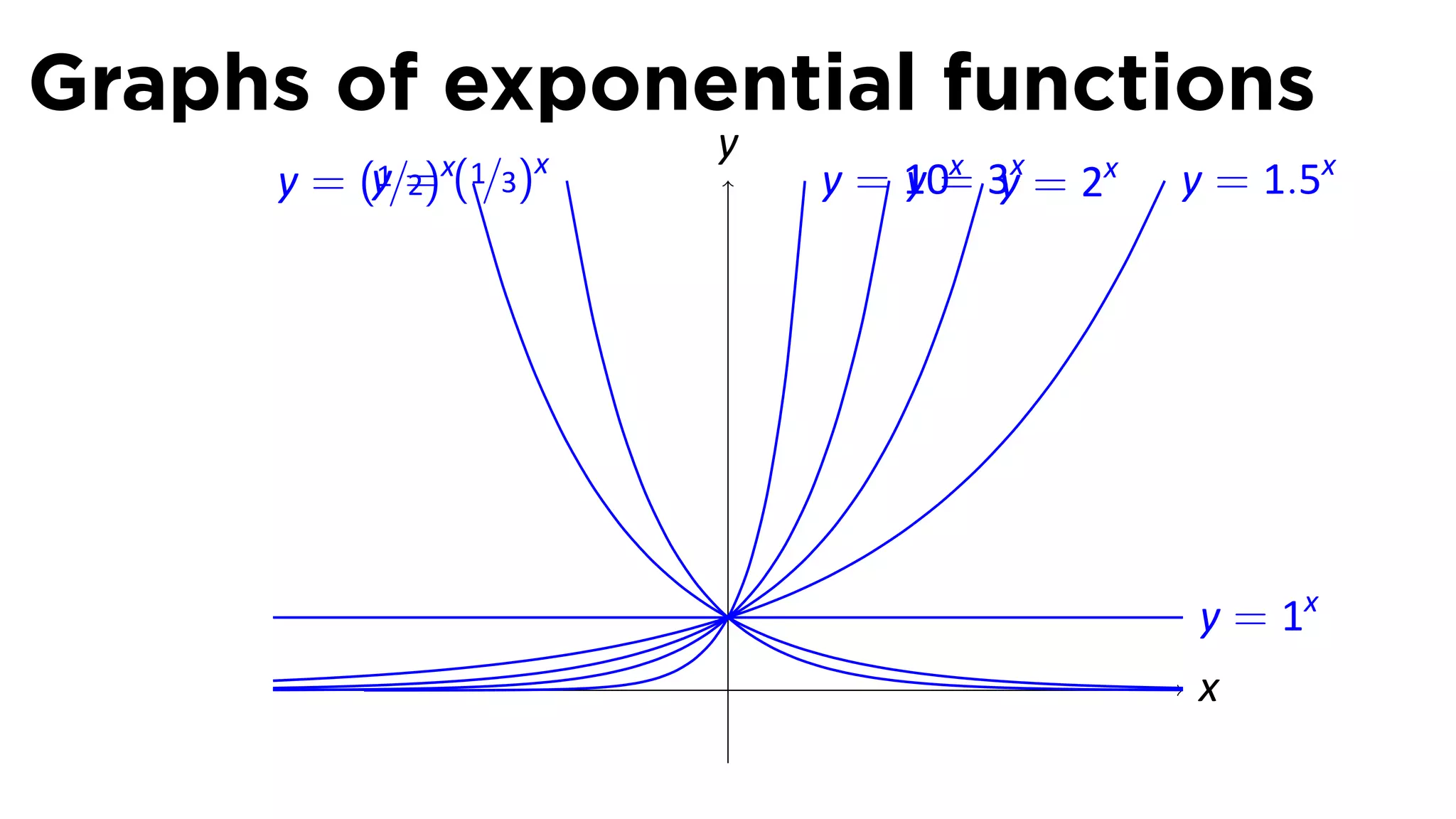
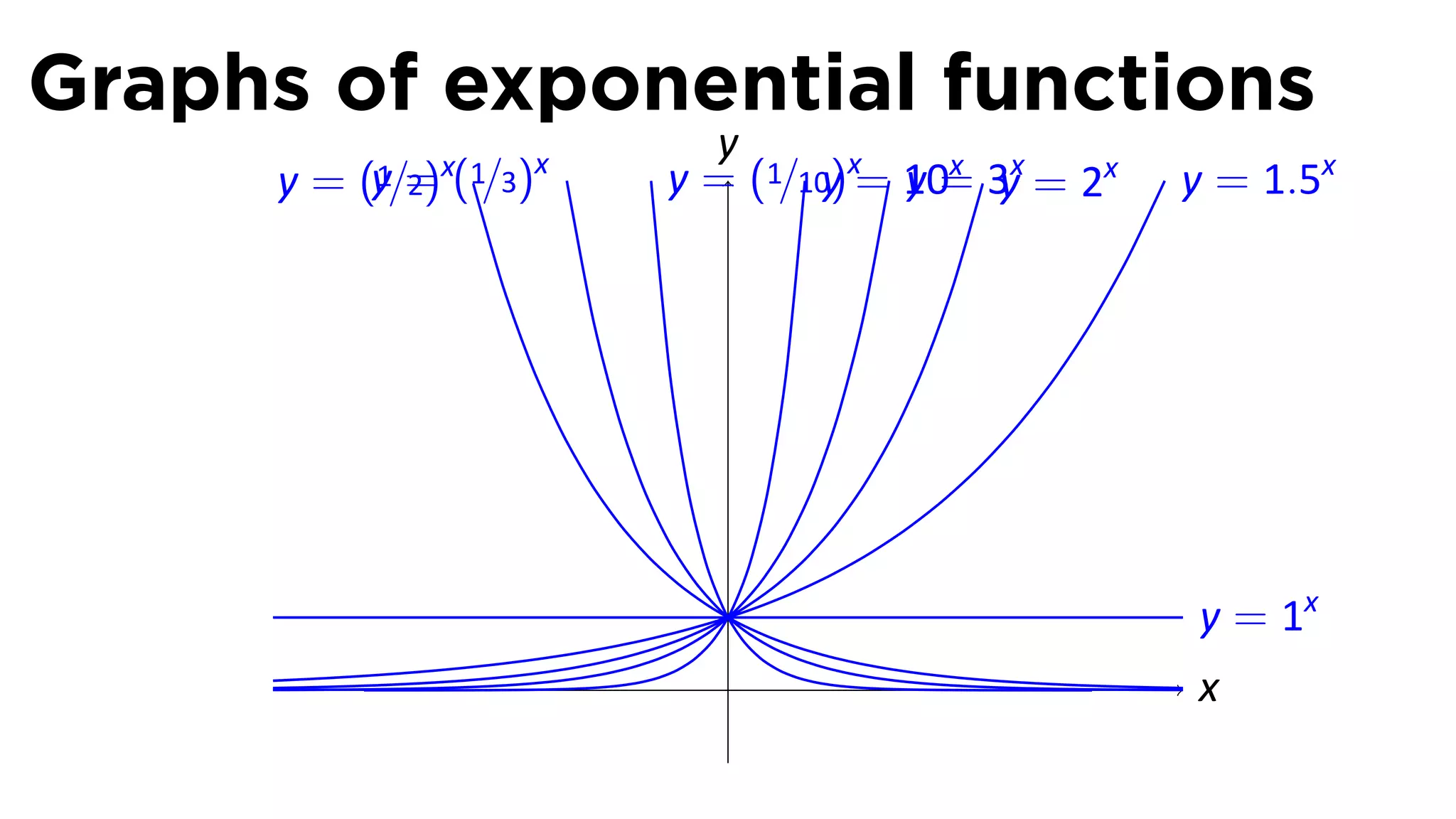
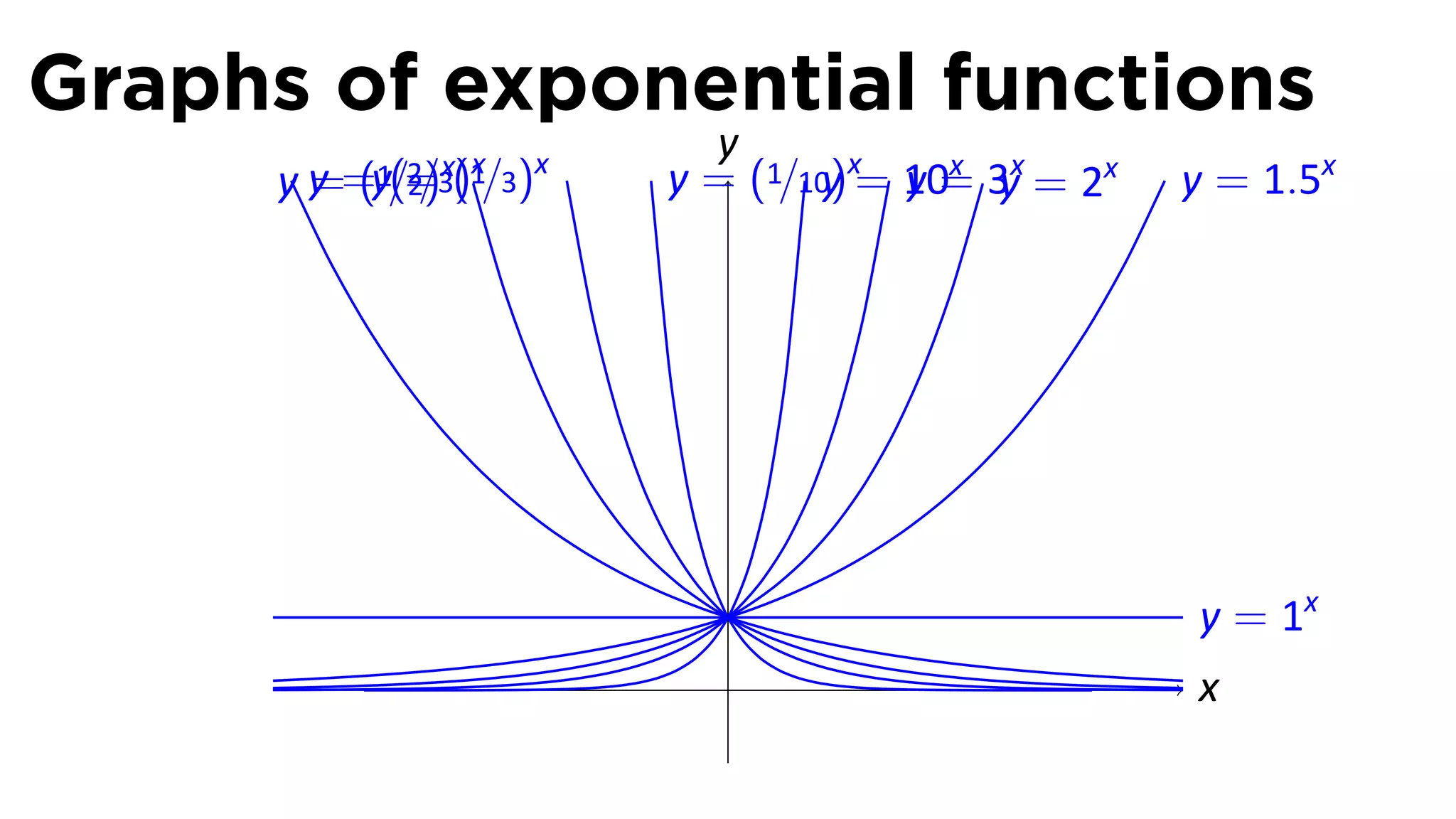
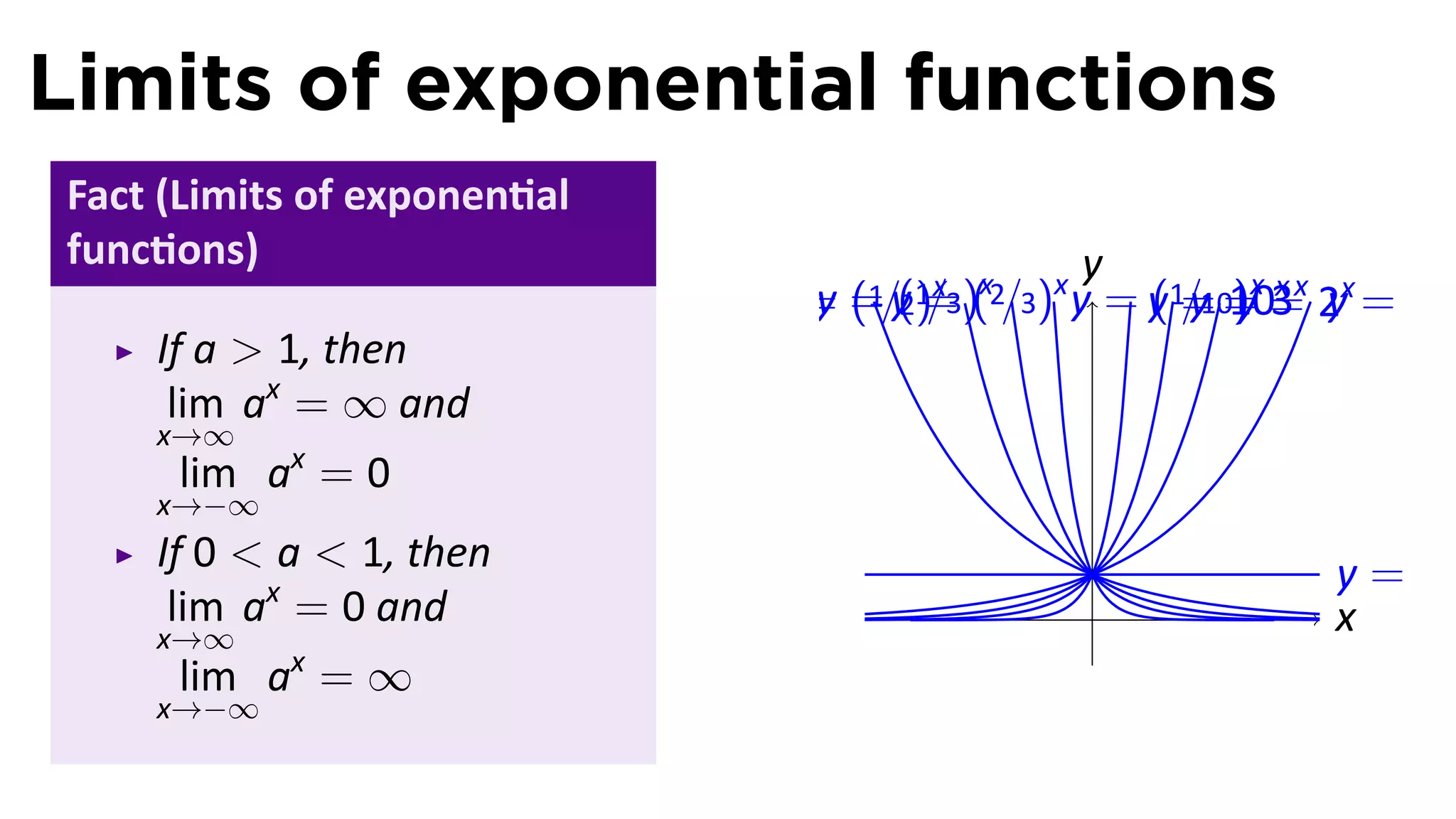
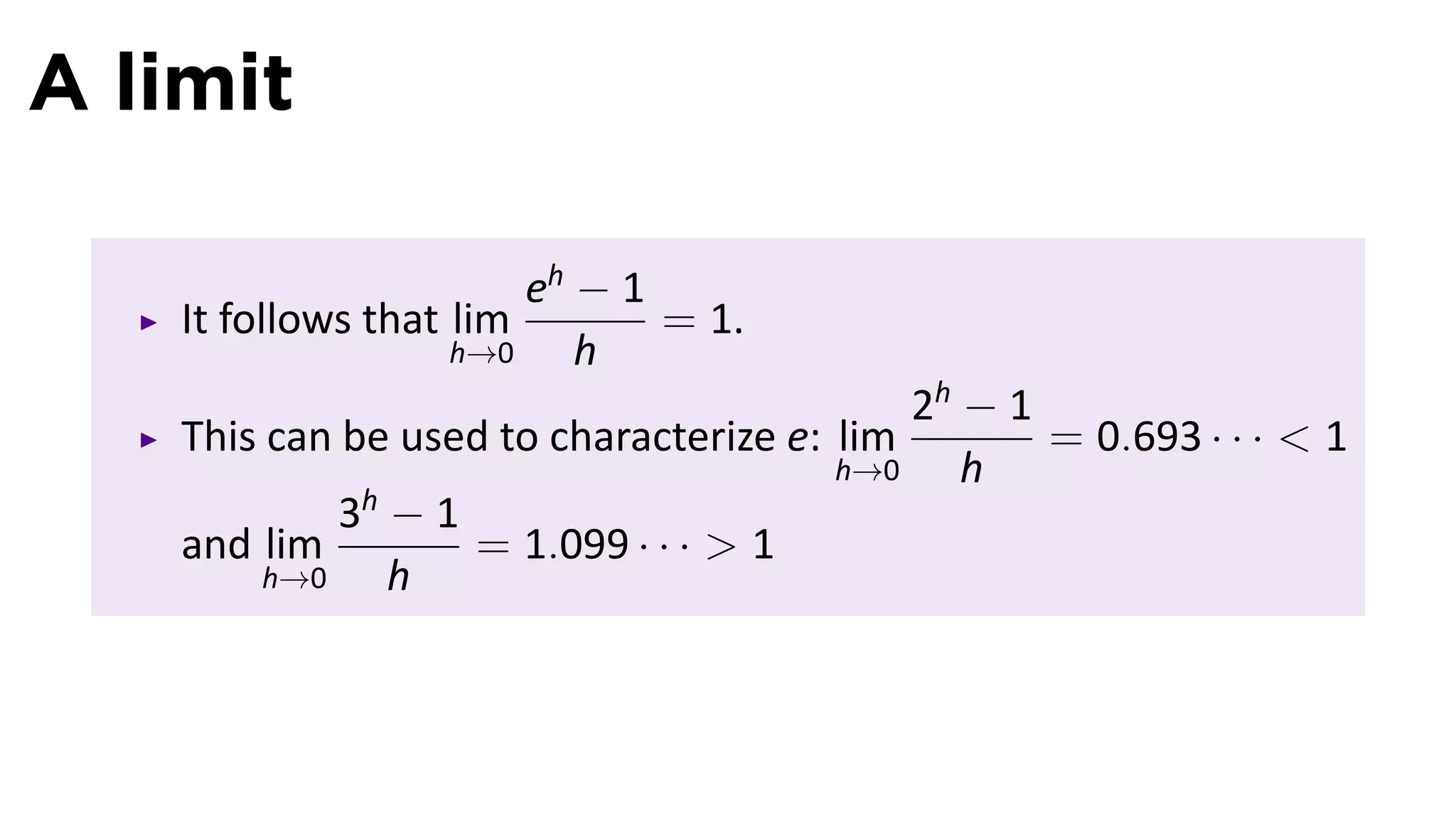The document provides an outline and definitions for sections 3.1 and 3.2 of a calculus class, which cover exponential and logarithmic functions. It defines exponential functions, establishes conventions for exponents of all types, and graphs exponential functions. Key points covered include the properties of exponential functions and defining exponents for non-whole number bases.




















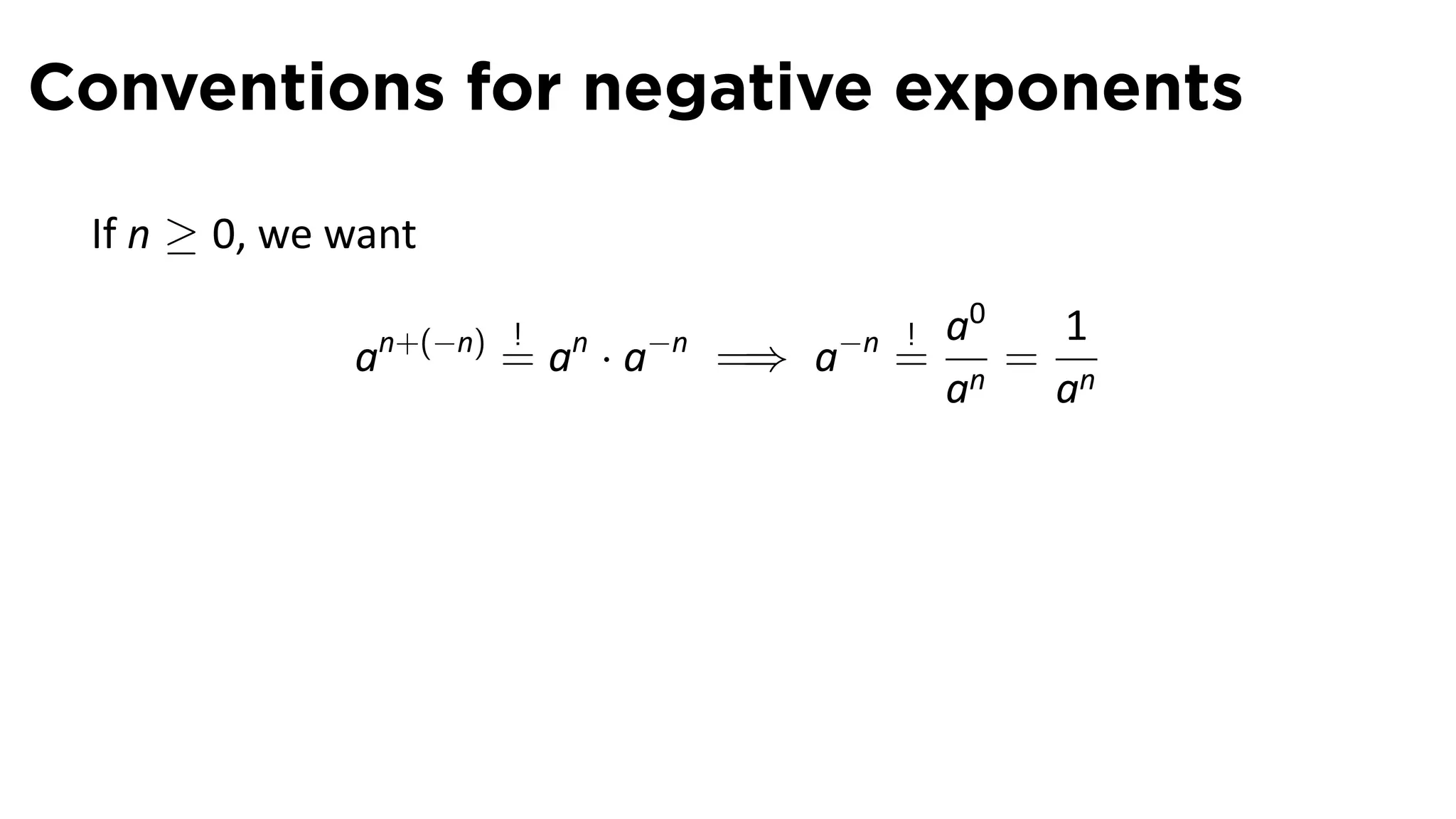


































![Compounded Interest: continuous
Ques on
Suppose you save P at interest rate r, with interest compounded
every instant. How much do you have a er t years?
Answer
( ( )rnt
r )nt 1
B(t) = lim P 1 + = lim P 1 +
n→∞ n n→∞ n
[ ( )n ]rt
1
= P lim 1 +
n→∞ n
independent of P, r, or t](https://image.slidesharecdn.com/lesson13-exponentialfunctions001slides-110315100550-phpapp02/75/Lesson-13-Exponential-and-Logarithmic-Functions-slides-69-2048.jpg)












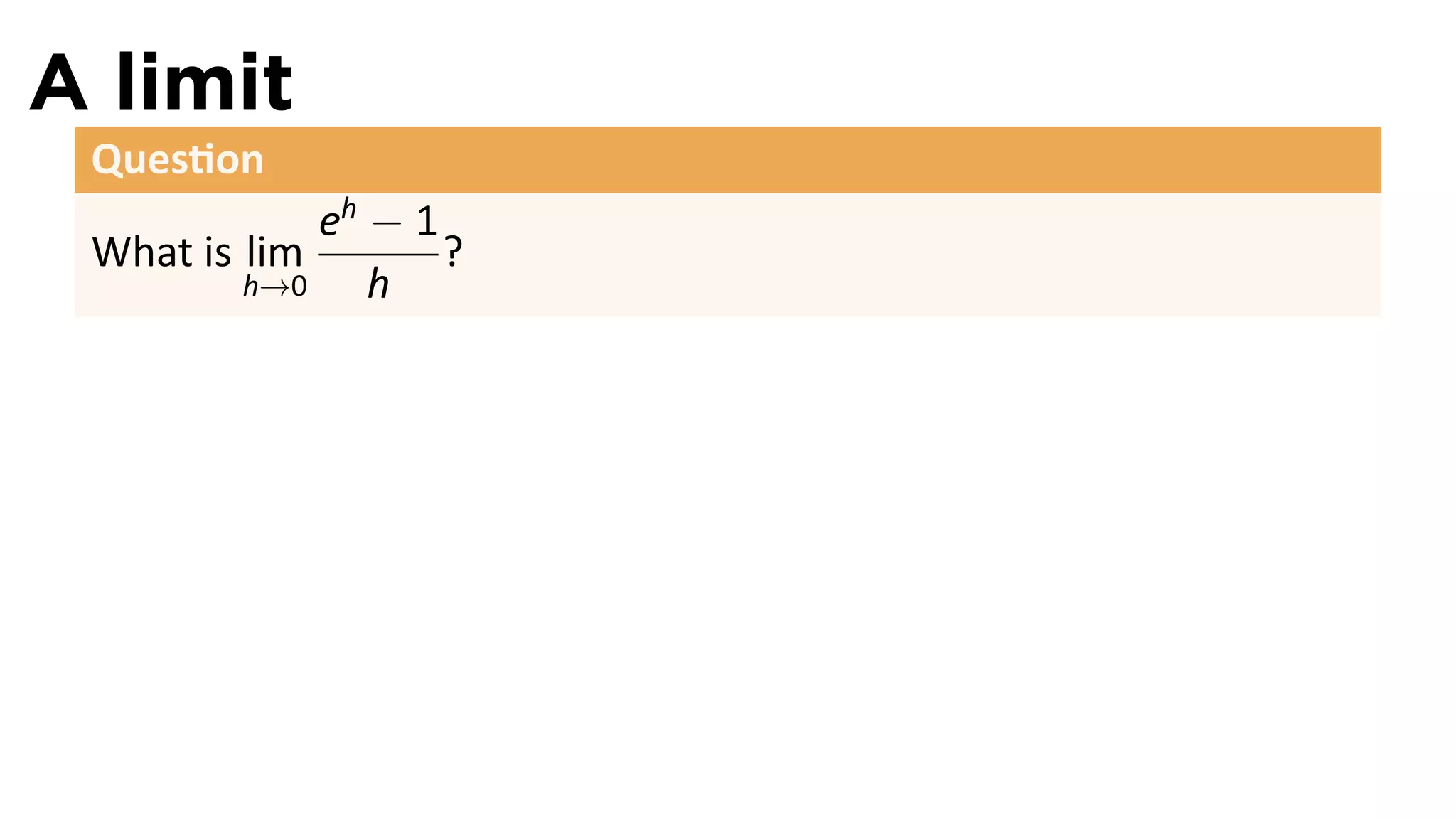
![A limit
Ques on
eh − 1
What is lim ?
h→0 h
Answer
e = lim (1 + 1/n)n = lim (1 + h)1/h . So for a small h,
n→∞ h→0
e ≈ (1 + h) 1/h
. So
[ ]h
eh − 1 (1 + h)1/h − 1
≈ =1
h h](https://image.slidesharecdn.com/lesson13-exponentialfunctions001slides-110315100550-phpapp02/75/Lesson-13-Exponential-and-Logarithmic-Functions-slides-83-2048.jpg)