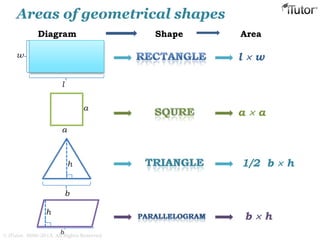
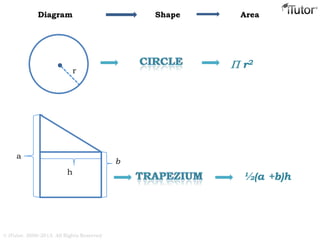
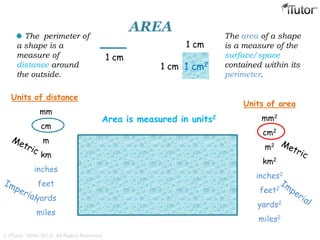
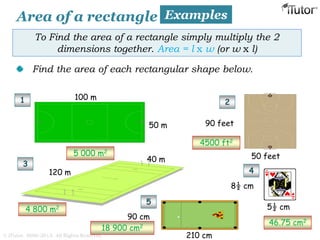
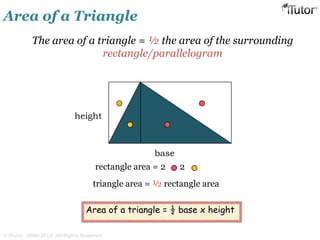
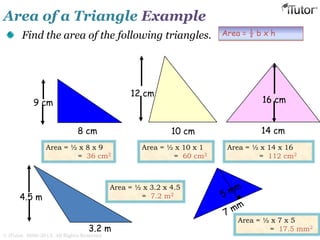
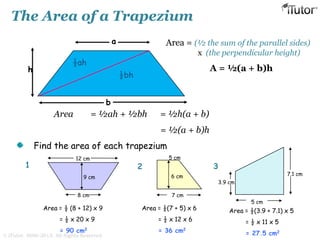
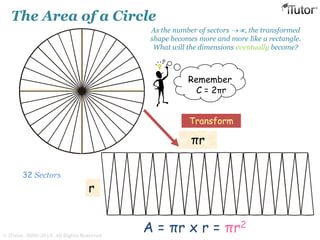
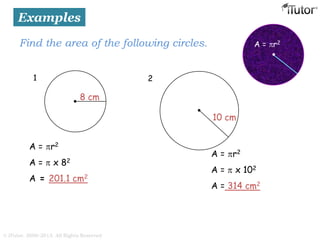
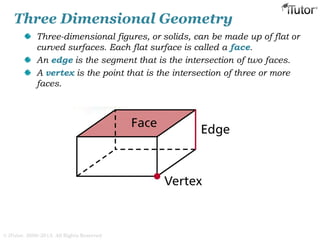
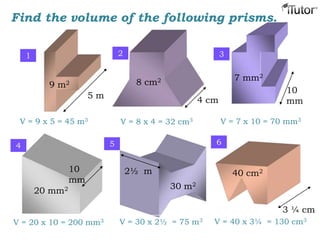
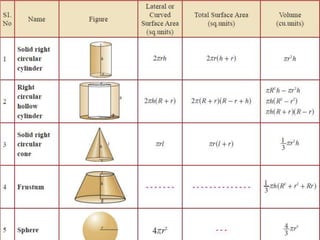
This document discusses mensuration, which is the use of formulas to calculate perimeters, areas, and volumes of plane and solid shapes. It provides formulas and examples for calculating the areas of rectangles, triangles, trapezoids, circles, and composite figures. It also discusses surface area and volume formulas for three-dimensional shapes like boxes, cylinders, prisms, pyramids, cones, spheres, and solids in general. Diagrams and step-by-step examples are provided to demonstrate calculating measurements of various shapes.