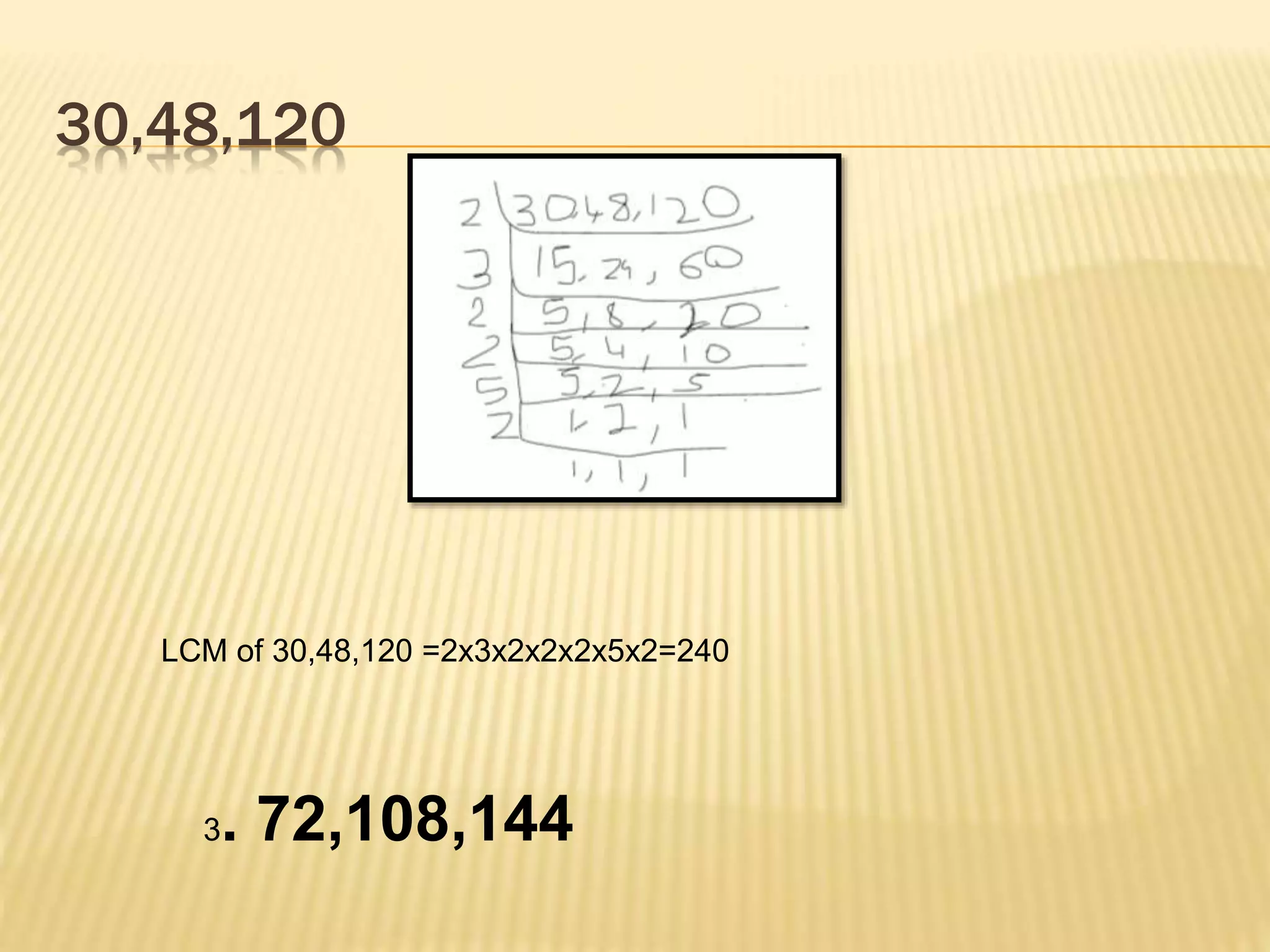
The document discusses prime factorization, HCF (highest common factor), and LCM (lowest common multiple). It explains that prime factorization is expressing a number as the product of prime numbers. There are factor tree and division methods for finding prime factors. HCF is the greatest number that divides two or more numbers. LCM is the lowest number that is a multiple of two or more numbers. Methods for finding HCF and LCM include prime factorization, common division, and long division. HCF and LCM are related in that the product of two numbers equals HCF times LCM.

1. CHAPTER 3
HCF AND LCM

2. PRIME FACTORIZATION
 It is the expression of a given number as the
product of prime numbers.
 It can be done using factor tree method or
division method.
 Fundamental Theorem of Arithmetic states
that every composite number has only one
factorization.

3. FACTOR TREE METHOD
 Draw the factor tree and write down the prime factorisation of the following
numbers
https://www.youtube.com/watch?v=tW97UU01ShY

4. PRIME FACTORIZATION THROUGH DIVISION
METHOD
 STEPS
Divide the number with a prime number
which will divide it exactly.
Continue dividing the quotient until you get a
quotient which is a prime number.

6. HCF (HIGHEST COMMON FACTOR)
 Highest common factor (H.C.F) of two or
more numbers is the greatest number
which divides each of them exactly. There
are many methods to find them.
1.listing the factors
2.HCF by Prime Factorization
3.HCF by Common division method
4. HCF by long division method.

7. FIND THE HCF OF FOLLOWING NUMBERS USING
THE METHOD OF LISTING FACTORS.
 24,30
24- 1,2,3,4,6,8,12,24
30- 1,2,3,5,6,10,15,30
COMMON FACTORS OF 24 AND 30- 1,2,3,6
HIGHEST COMMON FACTOR- 6
 24,72
24-1,2,3,4,6,8,12,24,
72-1,2,3,4,8,9,18,24,36,72
Common factors of 24and 72 are 1,2,3,4,8,24
Highest common factor- 24

8. Find the HCF of following numbers using the
method of Prime factorization.
 Step 1: find the prime factors of given
numbers.
 Step 2:find the common factors and circle
them.
 Step 3 multiply the common factors.

9. 30,96
 Prime factorization of 30- 2x3x5
 Prime factorization of 96- 2x2x2x2x3x2
 Hcf -2x3= 6

10. FINDING HCF BY COMMON DIVISION METHOD
STEP 1 -Divide all the three numbers by any
common factor.
STEP 2 - If there are still any common
factors, again divide the quotients by
them.
STEP 3 - Keep dividing until there is no
common factor.
STEP 4- The product of these common
factors will give the HCF.

11. Find the HCF of following numbers using the
method of division by common factors.
1. 12,18,24
2. 28,35,49
3. 32,64,96,128
4. 70,105,175

12. 1.12,18,24
HCF OF 12,18 and
24 is 3x2=6

13. 28,35,49
HCF OF 28,35 AND 49 IS 7.

14. 32,64,96,128
HCF OF 32,64,96 AND 128 = 8X4=32

15. FINDING HCF BY LONG DIVISION METHOD
Step 1.We divide the bigger number by smaller
one.
Step 2. Divide smaller number in step 1 with
remainder obtained in step 1.
Step 3. Divide divisor of second step with
remainder obtained in step 2.
Step 4. We will continue this process till we
get remainder zero and divisor obtained in
end is the required H.C.F.
https://www.youtube.com/watch?v=eljVa2KqOTo

16. Find the HCF of following numbers using the
method of long division.
1. 144,198
HCF of 144 and 198 is 18.

17. LCM(LOWEST COMMON MULTIPLE)
 The lowest common multiple of two or
more numbers is the lowest of their
common multiples.
 It is either equal to or greater than the
numbers.
 The two methods to find LCM are
1. Prime Factorization
2. Common division

18. LCM THROUGH PRIME FACTORIZATION
 Step 1- Do the prime factorization of all
the numbers.
 Step 2- Express it in terms of powers.
 Step 3- Multiply the highest powers of
each number.

19. FIND THE LCM USING PRIME FACTORIZATION.
 72,90
Prime Factorization of 72-2x2x2x3x3
= 23 x 32
Prime Factorization of 90 – 2x5x3x3
= 21x 51x 32
LCM of 72 and 90 = 23 x 32 x51
=2x2x2x3x3x5=360

20. b)16,30,42
Prime factorization of 16= 2x2x2x2=24
Prime factorization of 30=2x3x5= 21x31x51
prime factorization of 42= 2x3x7=21x31x71
lcm of 16,30 and 42 =24 x31 x 51x71
2x2x2x2x3x5x7
=4x4x15x7=16x105=1680

22. FIND THE LCM OF FOLLOWING NUMBERS BY
COMMON DIVISION METHOD.
1. 40,80,120,160
LCM of 40,80,120 and 160
=20x2x2x3x2=40x12=480

23. 30,48,120
LCM of 30,48,120 =2x3x2x2x2x5x2=240
3. 72,108,144

24. RELATIONSHIP BETWEEN HCF AND LCM
 The product of two numbers is the product of their HCF
and LCM.
 a x b= HCF x LCM
 a = HCF x LCM
b
 b = HCF x LCM
a
 HCF= a xb
LCM
 LCM= a xb
HCF

25.  The HCF of two numbers is 12 and their product
is 4320. What is their LCM? If one of the
numbers is 60, what is the other number?
HCF =12
Ax B=4320
LCM= AXB = 4320 =360
HCF 12
ONE NUMBER=60
THE OTHER NUMBER= 4320 =72
60
OR
B= HCF X LCM= 12X 360 = 4320 =72
A 60 60

26.  The HCF and LCM of two numbers is 15 and
450 respectively. If one number is 75, what
is the other number?
HCF= 15
LCM= 450
A= 75
 B= HCFX LCM =15X450 = 90
A 75