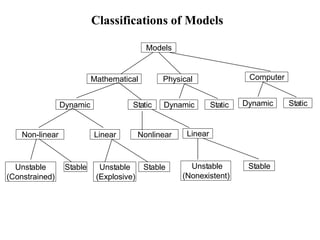
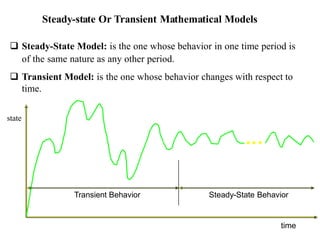
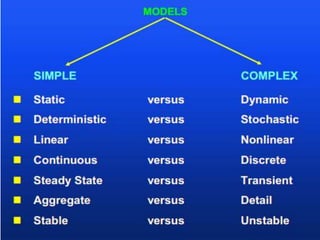
This document discusses different types of models used in computer science and engineering. It defines models as representations and abstractions of real or proposed systems. Models are classified as mathematical, physical, static, dynamic, linear, nonlinear, stable, unstable, analytical, numerical, descriptive, and prescriptive. Examples are provided for each type to illustrate the distinctions between mathematical, physical, static, dynamic, linear, nonlinear, stable, unstable, analytical, numerical, descriptive, and prescriptive models. Distributed-lag and autoregressive models are also introduced as special cases of regression models.

1. Department of Computer Science and Engineering
Hamdard University Bangladesh
All Types of Models

2.  A Model is a representation and abstraction of anything such as a
real system, a proposed system, a futuristic system design, an
entity, a phenomenon, or an idea.
Concepts of Models

3. Models
Mathematical Physical
Dynamic Static Dynamic Static
Non-linear Linear Nonlinear Linear
Unstable
(Constrained)
Stable Unstable
(Nonexistent)
StableUnstable
(Explosive)
Stable
Computer
Dynamic Static
Classifications of Models

4.  Mathematical Model: is the one in which symbols and logic constitute the
model. The symbolism used can be a language or a mathematical notation.
 A simulation model is built in terms of logic and mathematical equations
and is an abstract model.
 Physical Model: Physical model is a smaller or larger physical copy of an
object. The object being modeled may be small (for example, an atom) or large
(for example, the Solar System).
 A model of an airplane (scaled down), a model of the atom (scaled up), a
map, a globe, a model car are examples of physical (iconic) models.
Mathematical Vs. Physical Models

5.  Static Model: is the one which describes relationships that do not change with
respect to time.
 An architectural model of a house is a static physical model.
 An equation relating the lengths and weights on each side of a
playground variation is a static mathematical model.
 Static computer model which means fixed.
 Dynamic Model: is the one which describes time-varying
relationships.
 A wind tunnel is a dynamic physical model.
 The equations of motion of the planets around the sun constitute a
dynamic mathematical model of the solar system.
 Dynamic computer usually means capable of action and/or change.
Static Vs. Dynamic (Abstract /Physical/Computer) Models

6.  Analytical Model: is the one which is solved by using the deductive reasoning of
mathematical theory.
 A Linear Programming model, a Mixed Integer Linear Programming
model, a nonlinear optimization model are examples of analytical
models.
 Numerical Model: is the one which is solved by applying
computational procedures.
 Finding the roots of a nonlinear algebraic equation, f(x) = 0, using the
numerical model.
Analytical Vs. Numerical Mathematical Models

7.  Linear Model: is the one which describes relationships in linear
form.
 The equation 3x + 4z + 1=0 is a linear model.
 Nonlinear Model: is the one which describes relationships in
nonlinear form.
 The equation 2𝑥2 + 𝑦3—2=0 is a nonlinear model.
Linear Vs. Nonlinear Mathematical Models

8.  Stable Model: is the one which tends to return to its initial condition
after being disturbed.
 Like a simple pendulum.
 Unstable Model: is the one which may or may not come back to its
initial condition after being disturbed.
Stable Or Unstable Mathematical Models

9.  Steady-State Model: is the one whose behavior in one time period is
of the same nature as any other period.
 Transient Model: is the one whose behavior changes with respect to
time.
time
Transient Behavior Steady-State Behavior
Steady-state Or Transient Mathematical Models
state

10.  Descriptive Model: a system that represent a relationship but does not
indicate any course of action.
 The equation F (force) = M (mass) x A (acceleration) is a descriptive
model.
 All simulation models are descriptive models.
 Prescriptive or Normative Model: a system in that it prescribes the course
of action that the decision maker should take to achieve a defined objective.
 Decision analysis models are prescriptive.
Descriptive Vs. Prescriptive (Normative) Models

12.  If the regression model includes not only the current but
also the lagged (past) values of the explanatory variables
(the X’s) it is called a distributed-lag model.
 If the model includes one or more lagged values of the
dependent variable among its explanatory variables, it is
called an autoregressive model. This model is know as a
dynamic model.
Distributed-lag Model

13. Cobweb Model
 It is an economic model.
 In the model of supply and demand, the price adjusts so that the quantity
supplied and quantity demand are equal.
 The equilibrium is not always clear, so that some slopes are unstable.

14. Thats All !
Thanks for
listening...