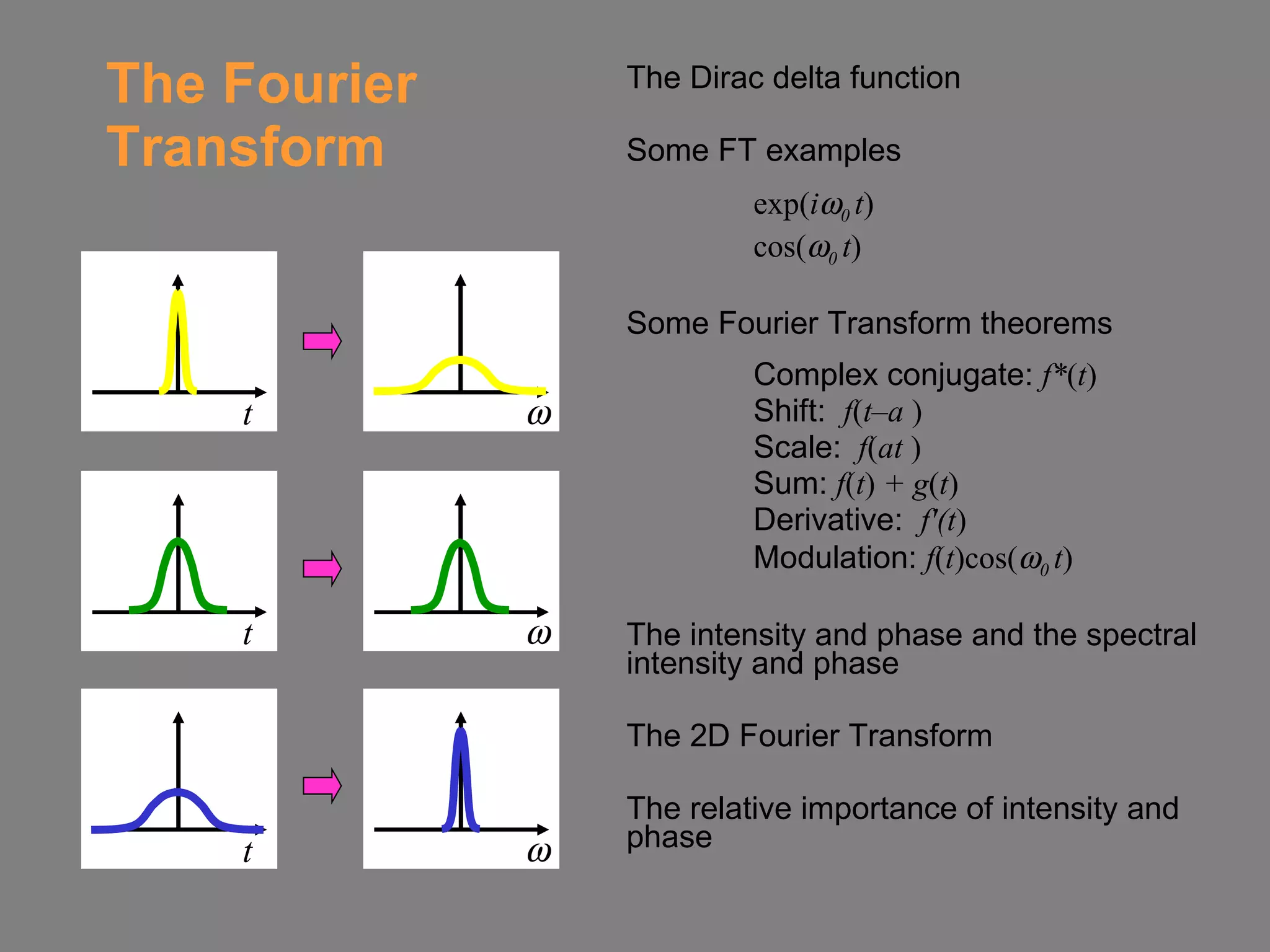
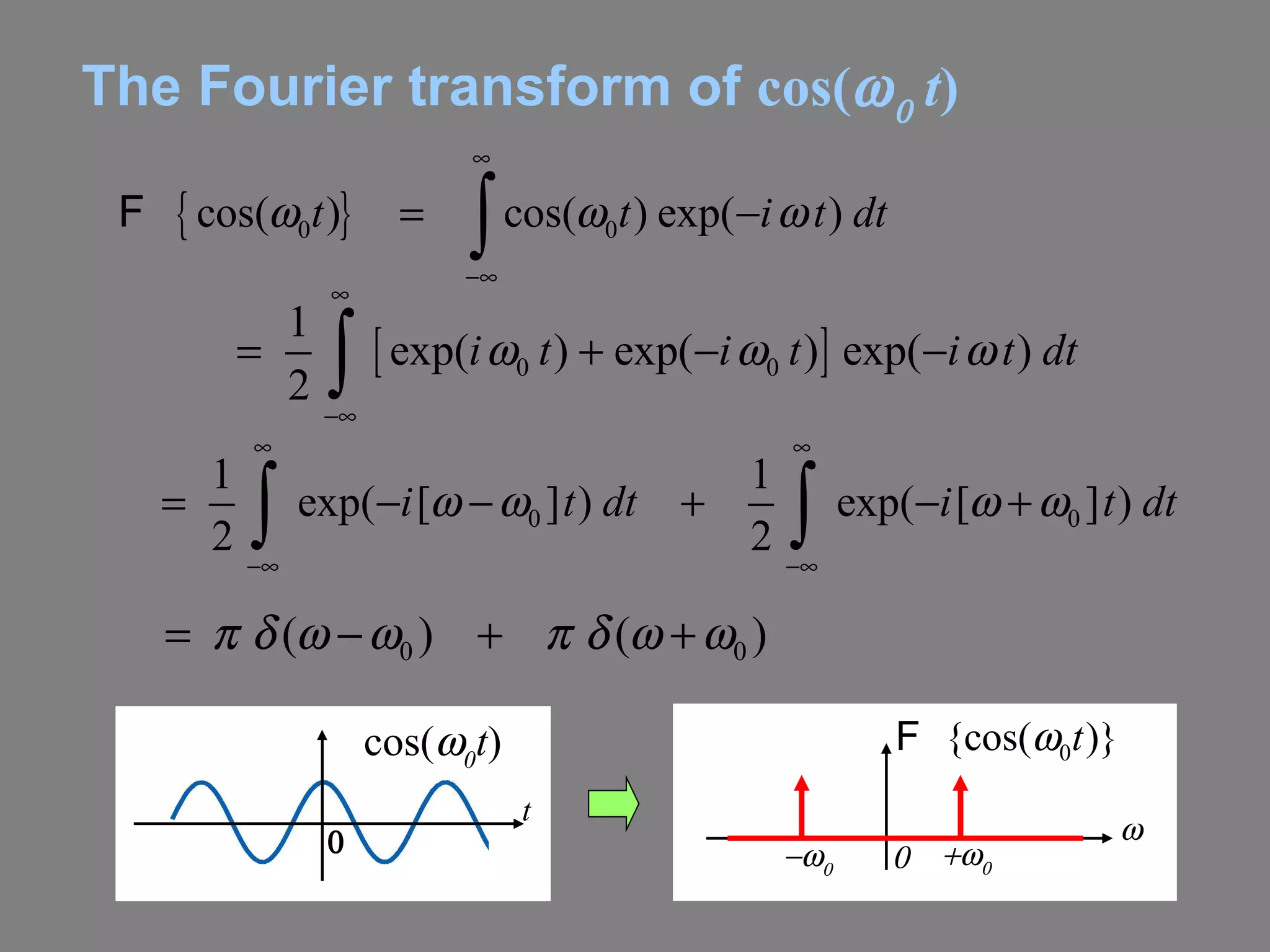
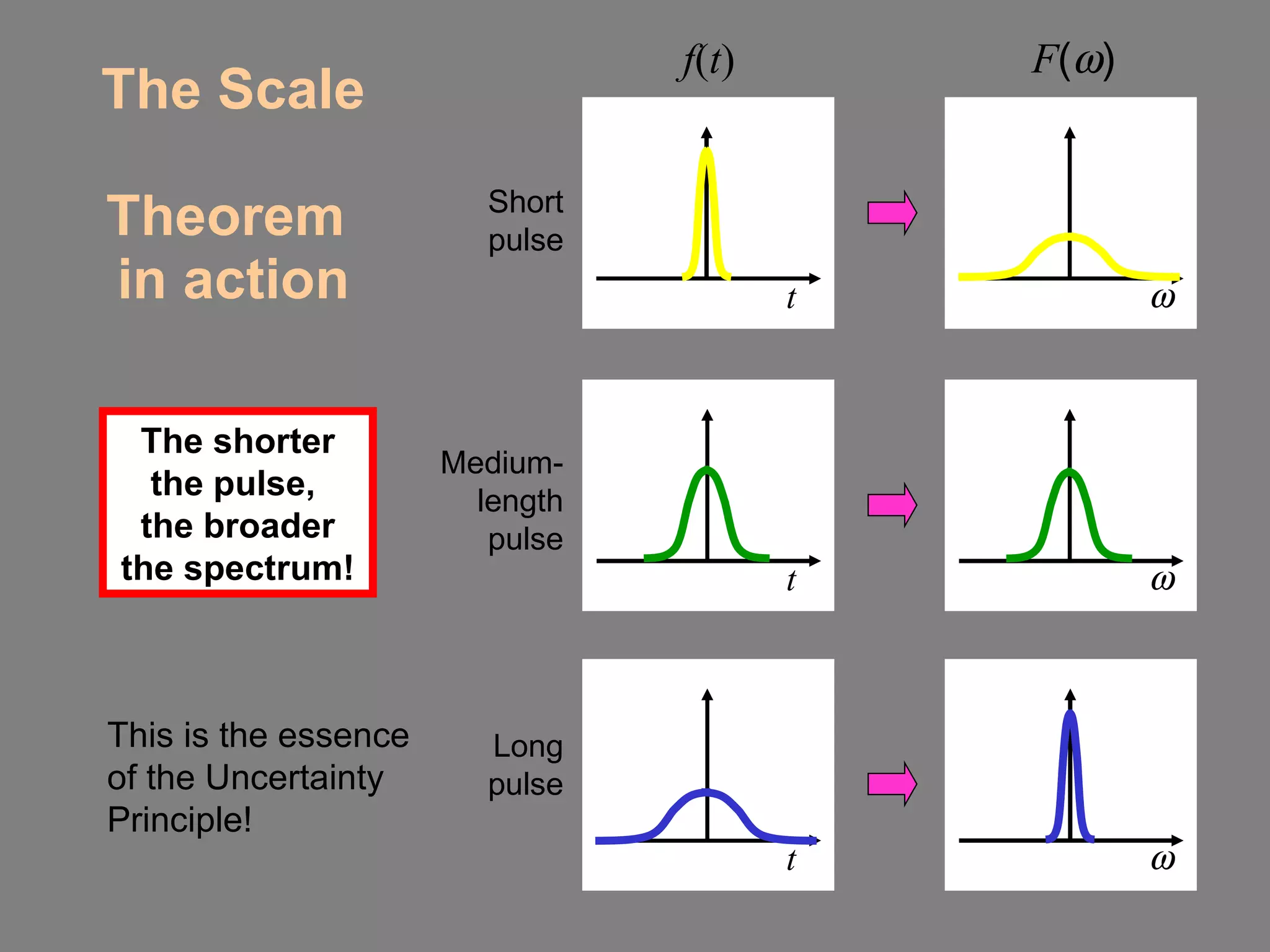
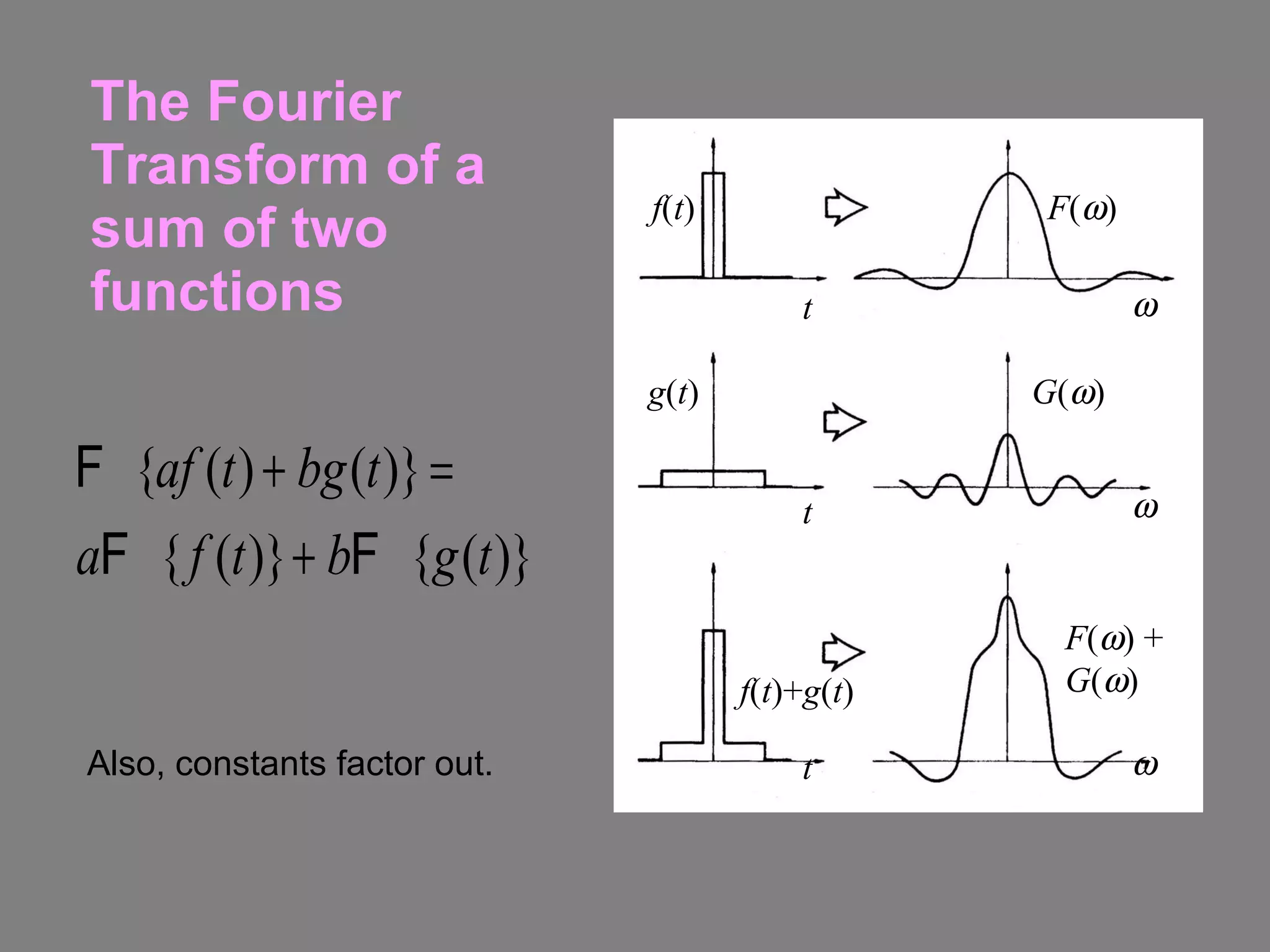
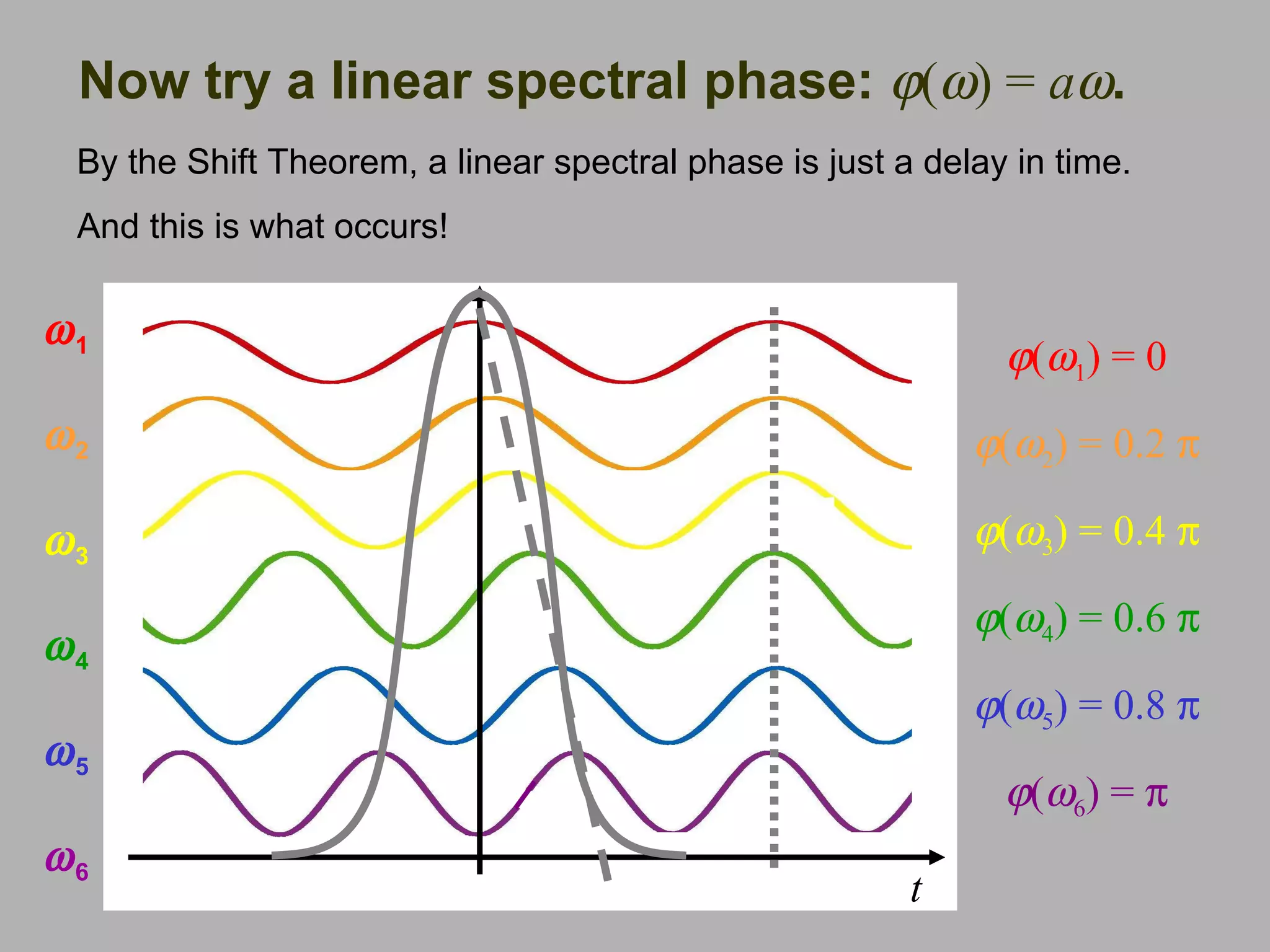
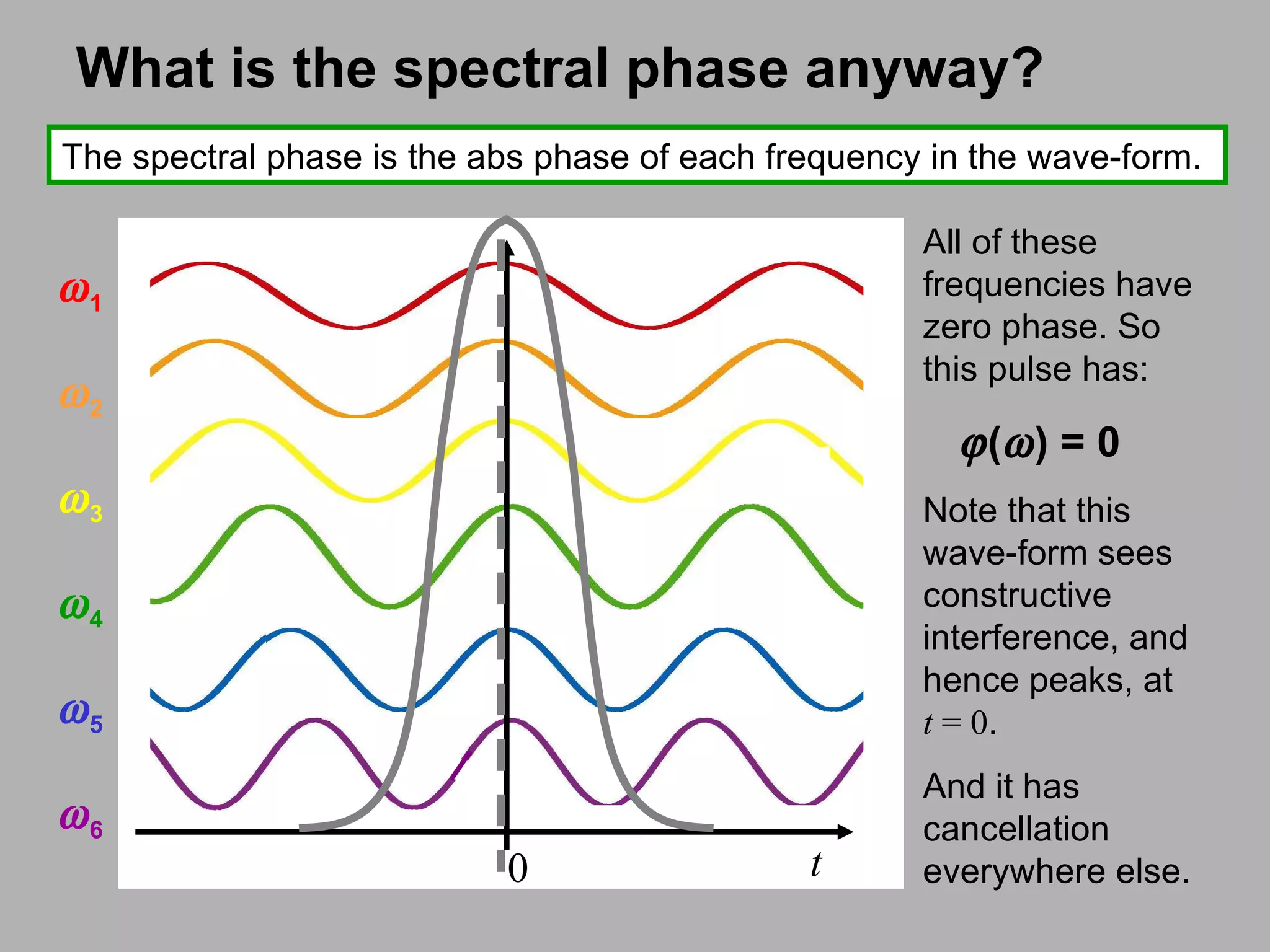
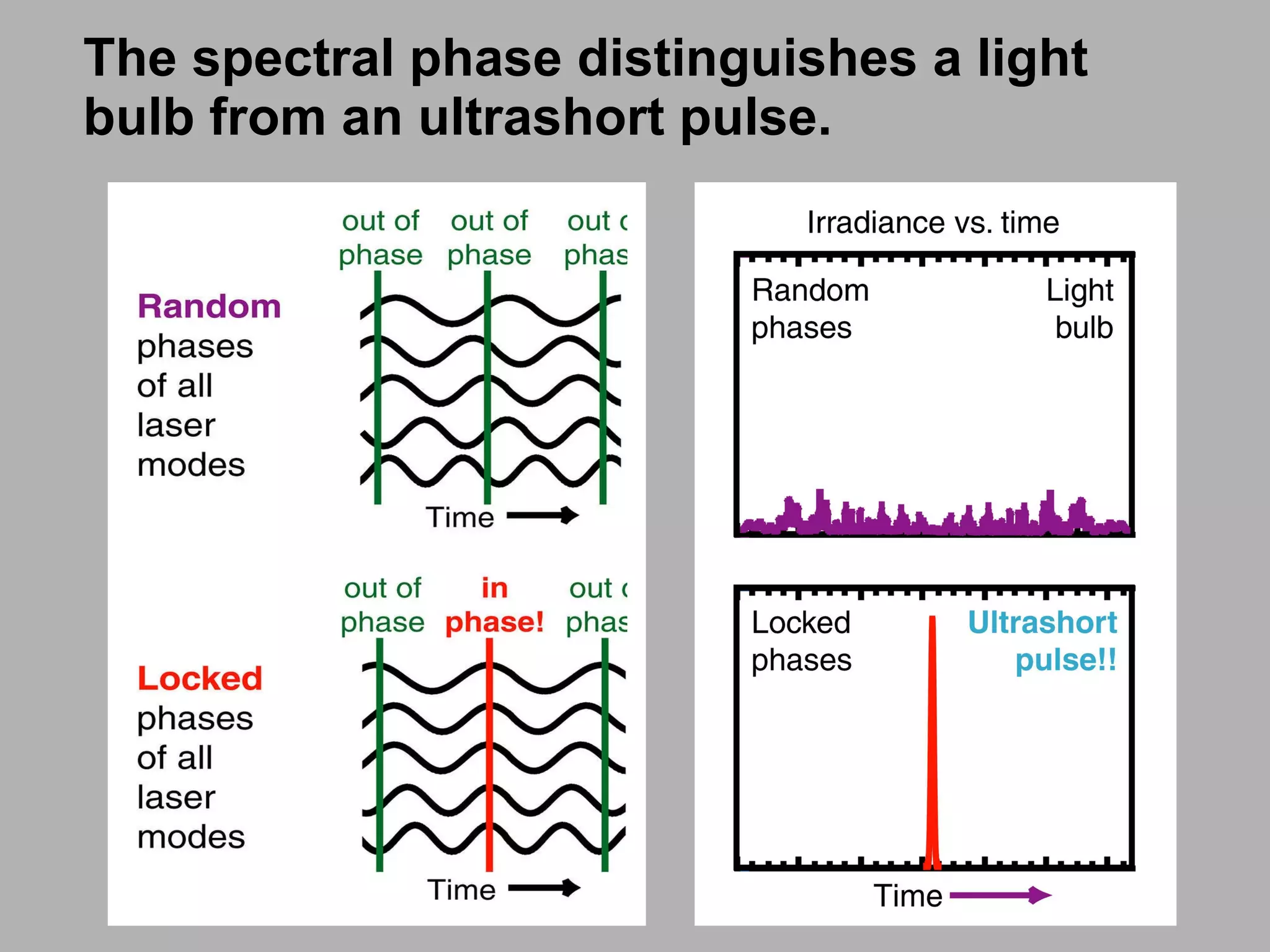
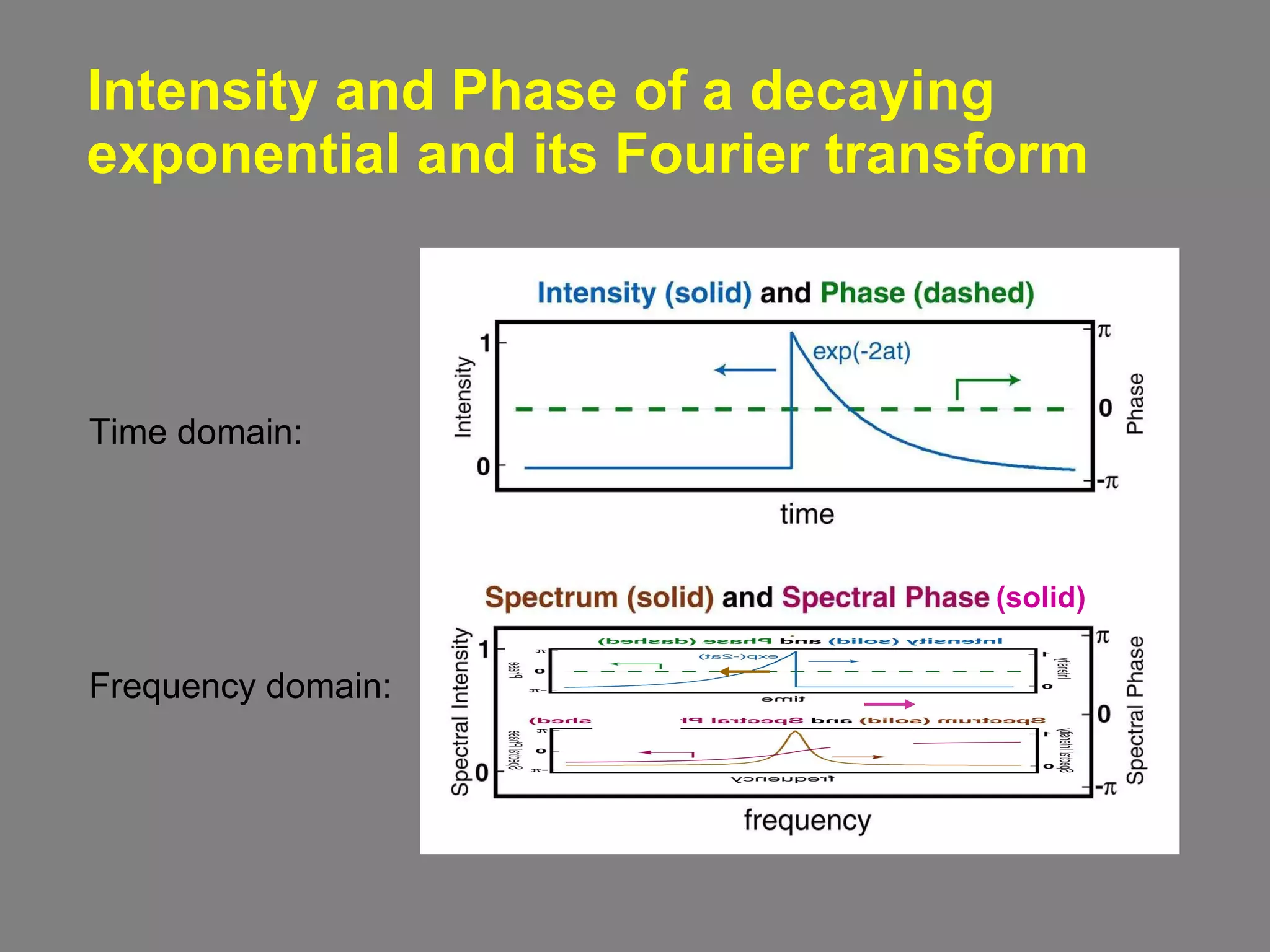
The document discusses several key concepts related to the Fourier transform: 1) It introduces the Dirac delta function and explains how it relates to the Fourier transform of exponential and cosine functions. 2) It describes several theorems regarding how the Fourier transform is affected by scaling, shifting, summing and differentiating functions. 3) It explains that both the intensity and phase of a time domain function, and the spectral intensity and phase in the frequency domain, are needed to fully characterize the function and its Fourier transform.

1. The Fourier Transform The Dirac delta function Some FT examples exp( i  0 t ) cos(  0 t ) Some Fourier Transform theorems Complex conjugate: f* ( t ) Shift: f ( t–a ) Scale: f ( at ) Sum: f ( t ) + g ( t ) Derivative: f'(t ) Modulation: f ( t )cos(  0 t ) The intensity and phase and the spectral intensity and phase The 2D Fourier Transform The relative importance of intensity and phase t t   t 

2. The Dirac delta function Unlike the Kronecker delta-function, which is a function of two integers, the Dirac delta function is a function of a real variable, t . t  ( t )

3. The Dirac delta function It’s best to think of the delta function as the limit of a series of peaked continuous functions. t f 1 ( t ) f m ( t ) = m exp[-( mt ) 2 ]/√  f 2 ( t ) f 3 ( t )  ( t )

4. Dirac  function Properties t  ( t )

5. The Fourier Transform and its Inverse

6. The Fourier Transform of  ( t ) is 1.   (  ) And the Fourier Transform of 1 is   (  ): t  ( t )   t 

7. The Fourier transform of exp( i  0 t ) The function exp( i  0 t ) is the essential component of Fourier analysis. It is a pure frequency. F {exp( i  0 t )}       exp( i  0 t )  t t Re Im 

8. The Fourier transform of cos(   t )           cos(  0 t ) t 

9. Scale Theorem The Fourier transform of a scaled function, f ( at ) : If a < 0 , the limits flip when we change variables, introducing a minus sign, hence the absolute value. Assuming a > 0 , change variables: u = at Proof:

10. The Scale Theorem in action f ( t ) F (  ) Short pulse Medium- length pulse Long pulse The shorter the pulse, the broader the spectrum! This is the essence of the Uncertainty Principle! t t   t 

11. The Fourier Transform of a sum of two functions Also, constants factor out. f ( t ) g ( t ) t t t    F (  ) G (  ) f ( t )+ g ( t ) F (  ) + G (  )

12. Shift Theorem

13. Application of the Shift Theorem Suppose we’re measuring the spectrum of E(t) , but a small fraction of its irradiance, say  , takes a longer path to the spectrometer. The extra light has the field, √  E(t–a) , where a is the extra path. The measured spectrum is: Performing the Fourier Transform and using the Shift Theorem: E ( t ) Spectro-meter E ( t )  E ( t-a )

14. Application of the Shift Theorem (cont’d) Neglecting  compared to  √  and 1: The contaminated spectrum will have ripples with a period of 2  / a . And these ripples will have a surprisingly large amplitude. If  = 1% (a seemingly small amount), these ripples will have an amazingly large amplitude of 2 √  = 20% !

15. The Fourier Transform of the complex conjugate of a function Proof:

16. Derivative Theorem The Fourier transform of a derivative of a function, f’(t) : Proof: Integrate by parts:

17. The Modulation Theorem: The Fourier Transform of E ( t ) cos(  0 t ) If E ( t ) =  ( t ) , then:   0  -  0

18. The Fourier transform and its inverse are symmetrical: f ( t ) F (  ) and F ( t ) f (  ) (almost). If f(t) Fourier transforms to F (  ), then F(t) Fourier transforms to: Relabeling the integration variable from t to  ’, we can see that we have an inverse Fourier transform: This is why it is often said that f and F are a “Fourier Transform Pair.” Rearranging:

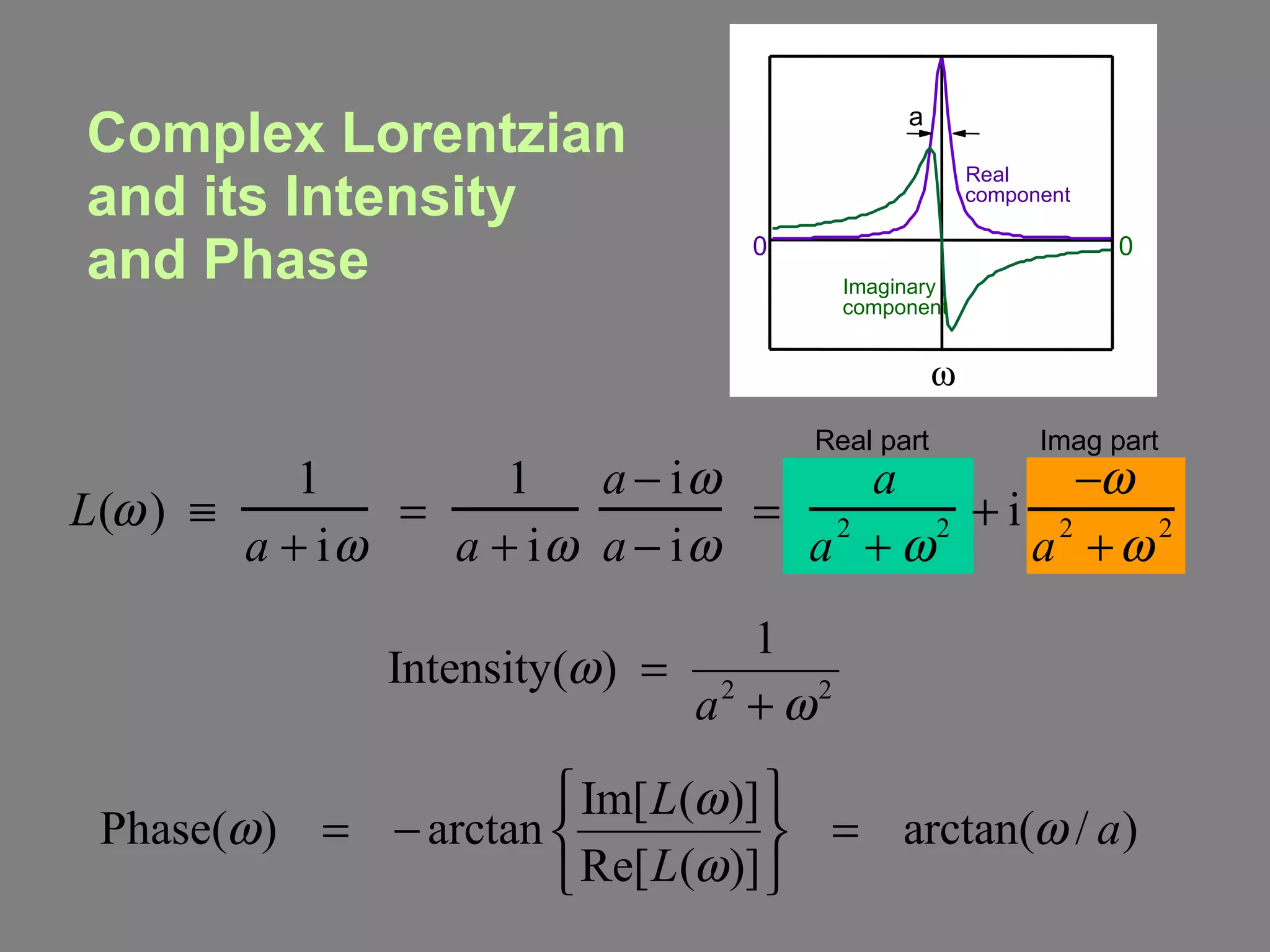
19. Fourier Transform Magnitude and Phase As with any complex quantity, we can decompose f ( t ) and F (  ) into their magnitude and phase. f ( t ) can be written: f ( t ) = Mag { f ( t ) } exp[ - i Phase { f ( t )} ] where Mag { f ( t ) } 2 is often called the intensity, I ( t ) , and Phase { f ( t ) } is called the phase,  ( t ) . They’re the same quantities we’re used to for light waves. Analogously, F (  ) = Mag { F (  ) } exp[ - i Phase { F (  ) } ] The Mag { F (  ) } 2 is called the spectrum, S (  ) , and the Phase { F (  ) } is called the spectral phase,  (  ) . Just as both the intensity and phase are required to specify f ( t ) , both the spectrum and spectral phase are required to specify F (  ) , and hence f ( t ) .

20. Calculating the Intensity and the Phase It’s easy to go back and forth between the electric field and the intensity and phase. The intensity:  (t) = -Im{ ln[ E (t)  ] } The phase: Equivalently,  (t i ) Re Im E(t i ) √ I(t i ) I(t) = |E(t)| 2

21. Intensity and Phase of a Gaussian The Gaussian is real, so its phase is zero. Time domain: Frequency domain: So the spectral phase is zero, too. A Gaussian transforms to a Gaussian

22. The spectral phase of a time-shifted pulse Recall the Shift Theorem: So a time-shift simply adds some linear spectral phase to the pulse! Time-shifted Gaussian pulse (with a flat phase):

23. What is the spectral phase anyway? The spectral phase is the abs phase of each frequency in the wave-form. 0 All of these frequencies have zero phase. So this pulse has:  (  ) = 0 Note that this wave-form sees constructive interference, and hence peaks, at t = 0 . And it has cancellation everywhere else.  1  2  3  4  5  6 t

24. Now try a linear spectral phase:  (  ) = a  . t  (  1 ) = 0  (  2 ) = 0.2   (  3 ) = 0.4   (  4 ) = 0.6   (  5 ) = 0.8   (  6 ) =   1  2  3  4  5  6 By the Shift Theorem, a linear spectral phase is just a delay in time. And this is what occurs!

25. The spectral phase distinguishes a light bulb from an ultrashort pulse.

26. Complex Lorentzian and its Intensity and Phase  0 Imaginary component Real component 0 a Real part Imag part

27. Intensity and Phase of a decaying exponential and its Fourier transform Time domain: Frequency domain: (solid)

28. Light has intensity and phase also. A light wave has the time-domain electric field: Intensity Phase Equivalently, vs. frequency: Spectral Phase (neglecting the negative-frequency component) Spectrum Knowledge of the intensity and phase or the spectrum and spectral phase is sufficient to determine the light wave. The minus signs are just conventions. We usually extract out the carrier frequency.

29. Fourier Transform with respect to space F { f ( x )} = F ( k ) If f ( x ) is a function of position, We refer to k as the “spatial frequency.” Everything we’ve said about Fourier transforms between the t and  domains also applies to the x and k domains. x k

30. The 2D Fourier Transform F (2) { f ( x,y )} = F ( k x ,k y ) = f ( x,y ) exp[- i ( k x x+k y y )] dx dy If f ( x,y ) = f x ( x ) f y ( y ) , then the 2D FT splits into two 1D FT's. But this doesn’t always happen. F (2) { f ( x,y )} x y f ( x,y )

31. A 2D Fourier Transform: a square function Consider a square function in the xy plane: f ( x,y ) = rect( x ) rect( y ) The 2D Fourier Transform splits into the product of two 1D Fourier Transforms: F { f ( x,y )} = sinc( k x /2 ) sinc( k y /2 ) This picture is an optical determination of the Fourier Transform of the square function! F (2) { f ( x,y )} x y f ( x,y )

32. Fourier Transform Magnitude and Phase Pictures reconstructed using the spectral phase of the other picture The phase of the Fourier transform (spectral phase) is much more important than the magnitude in reconstructing an image. Mag{ F [Linda]} Phase{ F [Rick]} Mag{ F [Rick]} Phase{ F {Linda]} Rick Linda