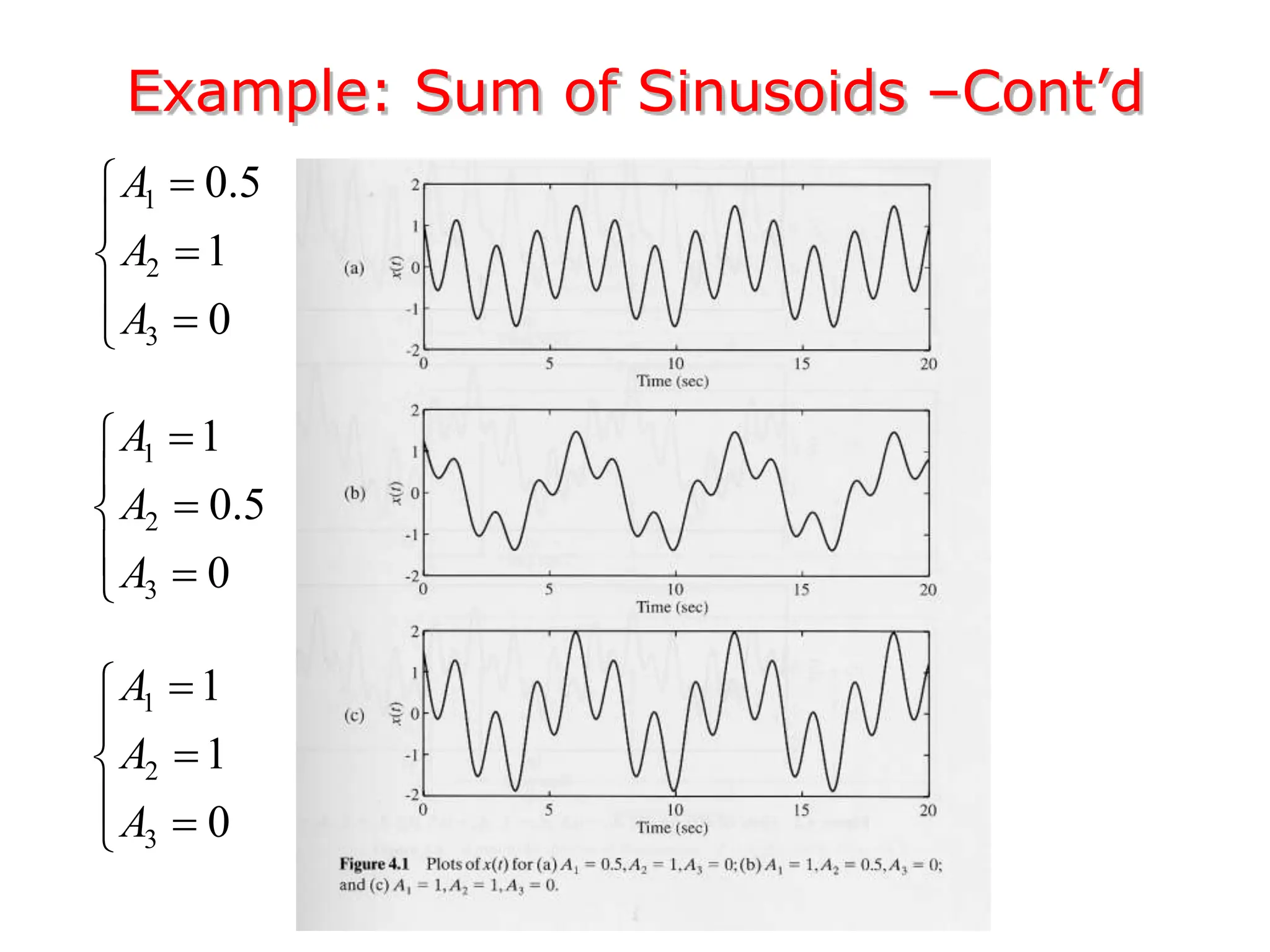
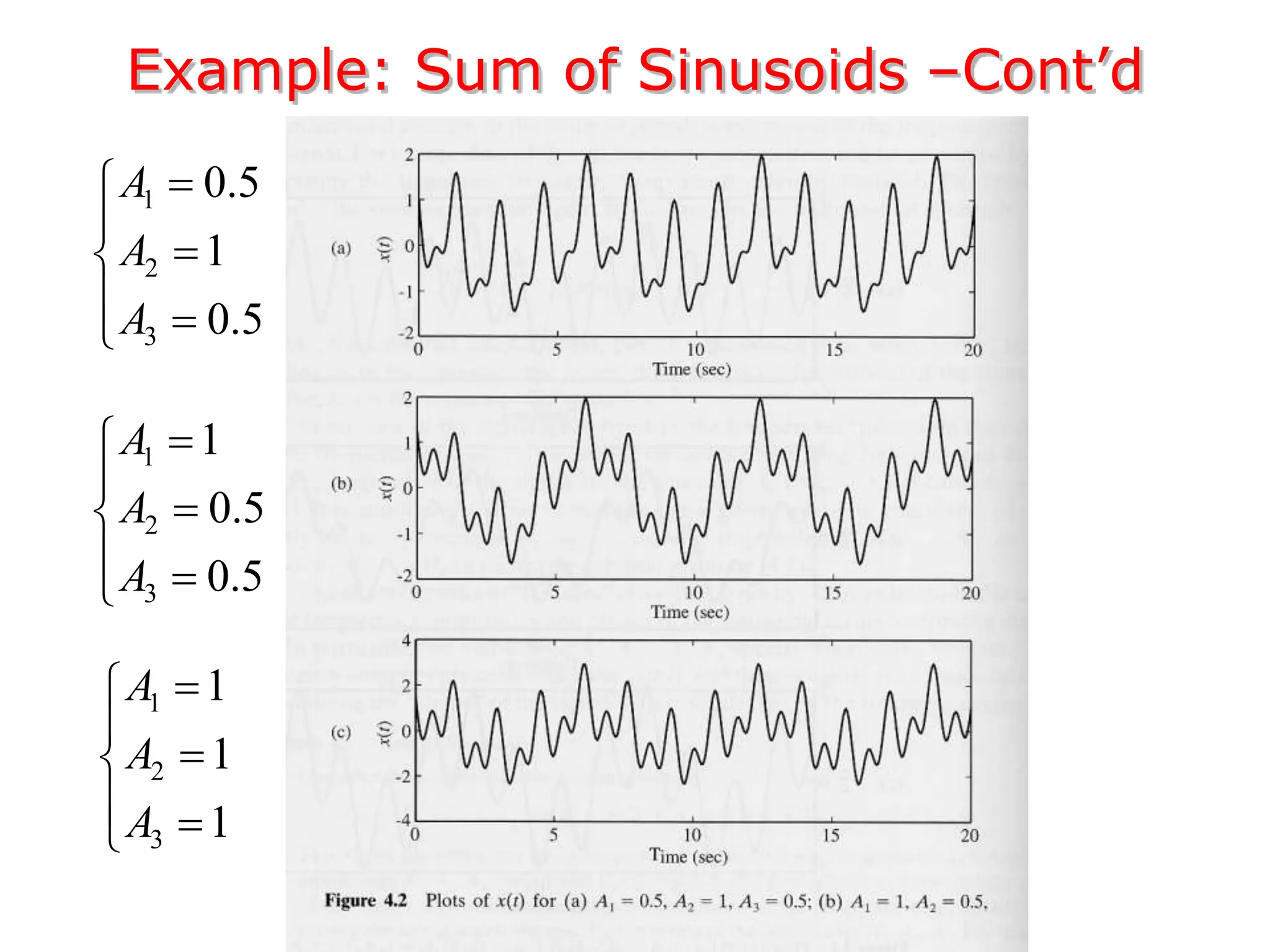
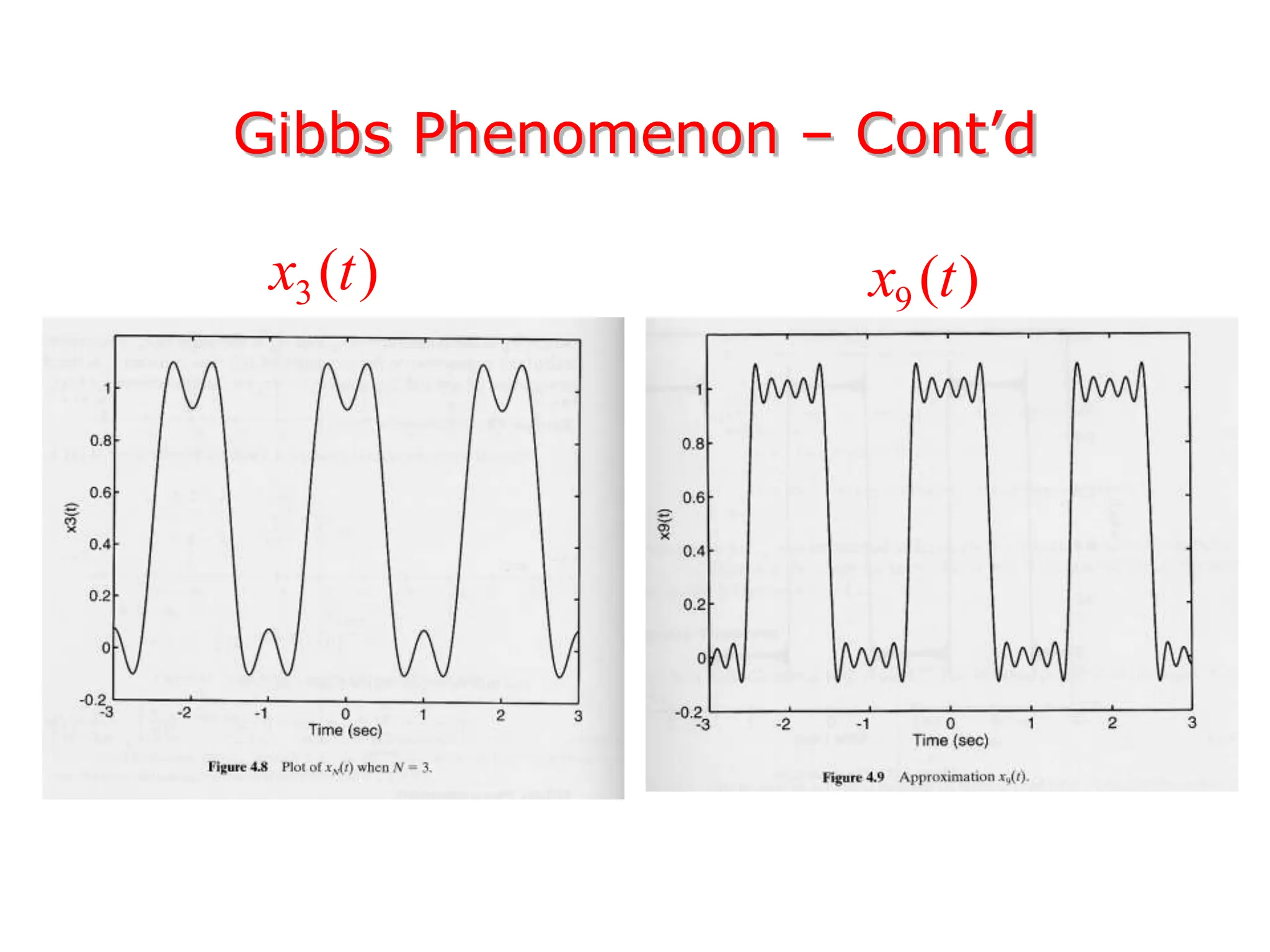
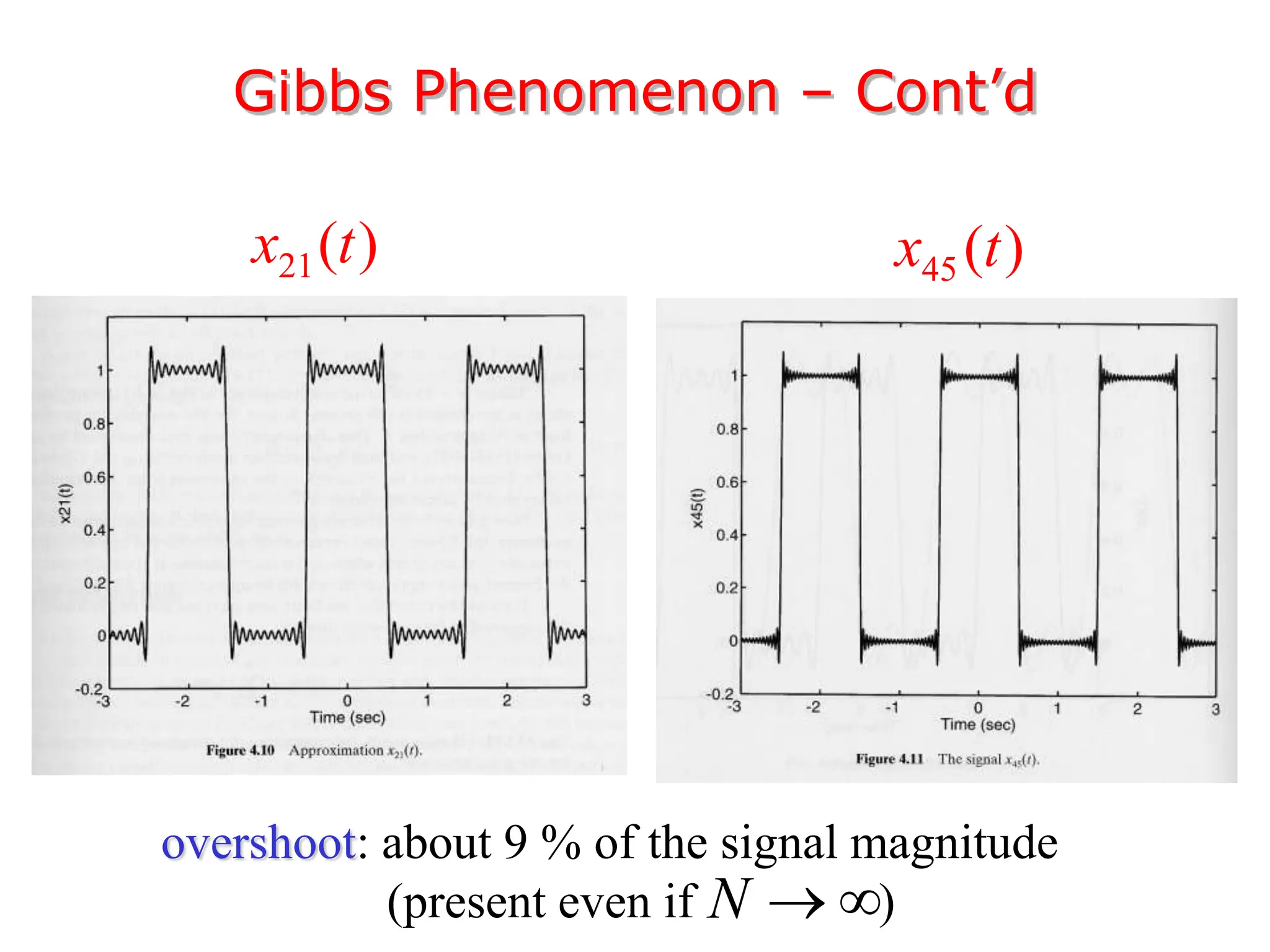
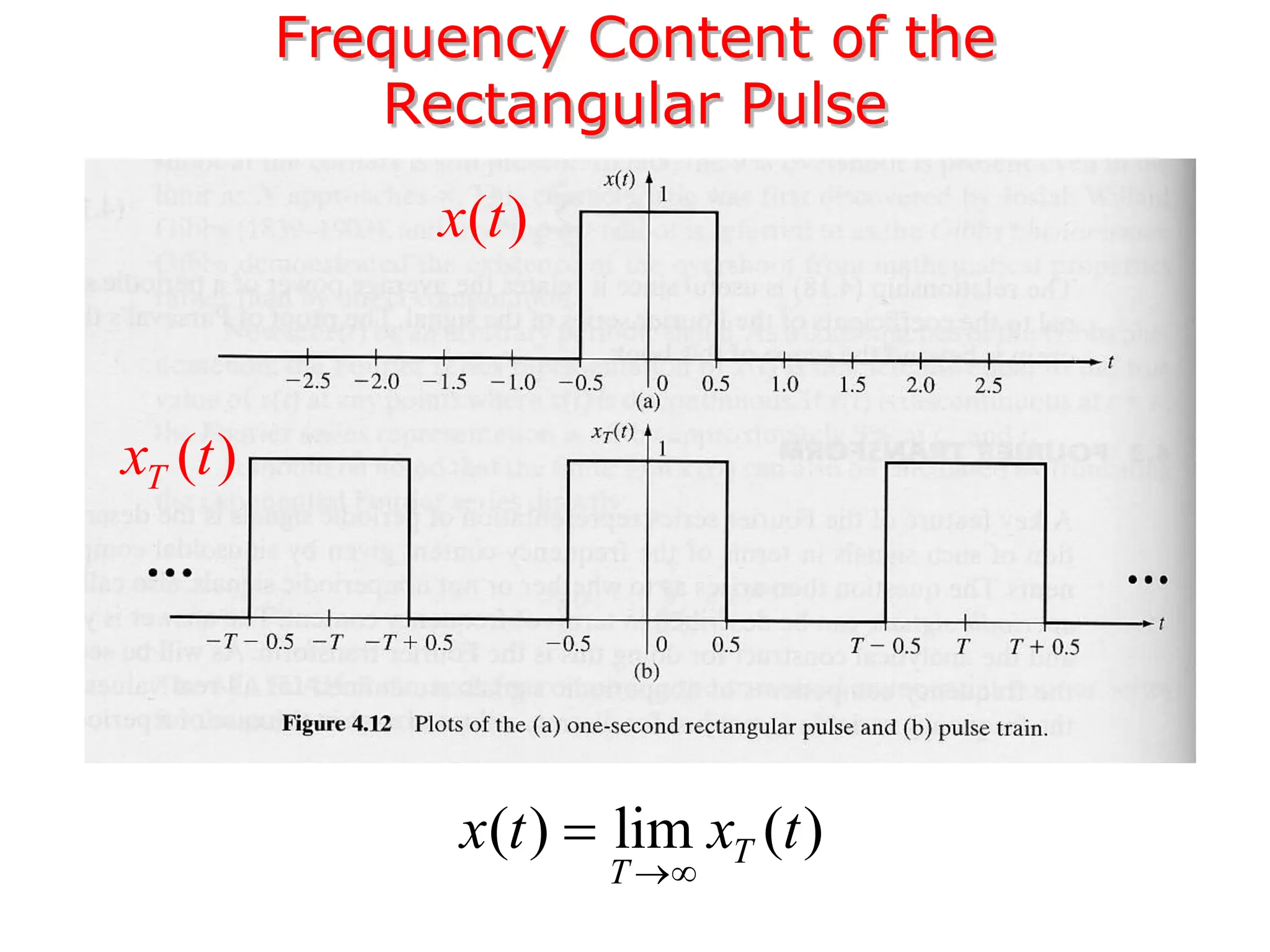
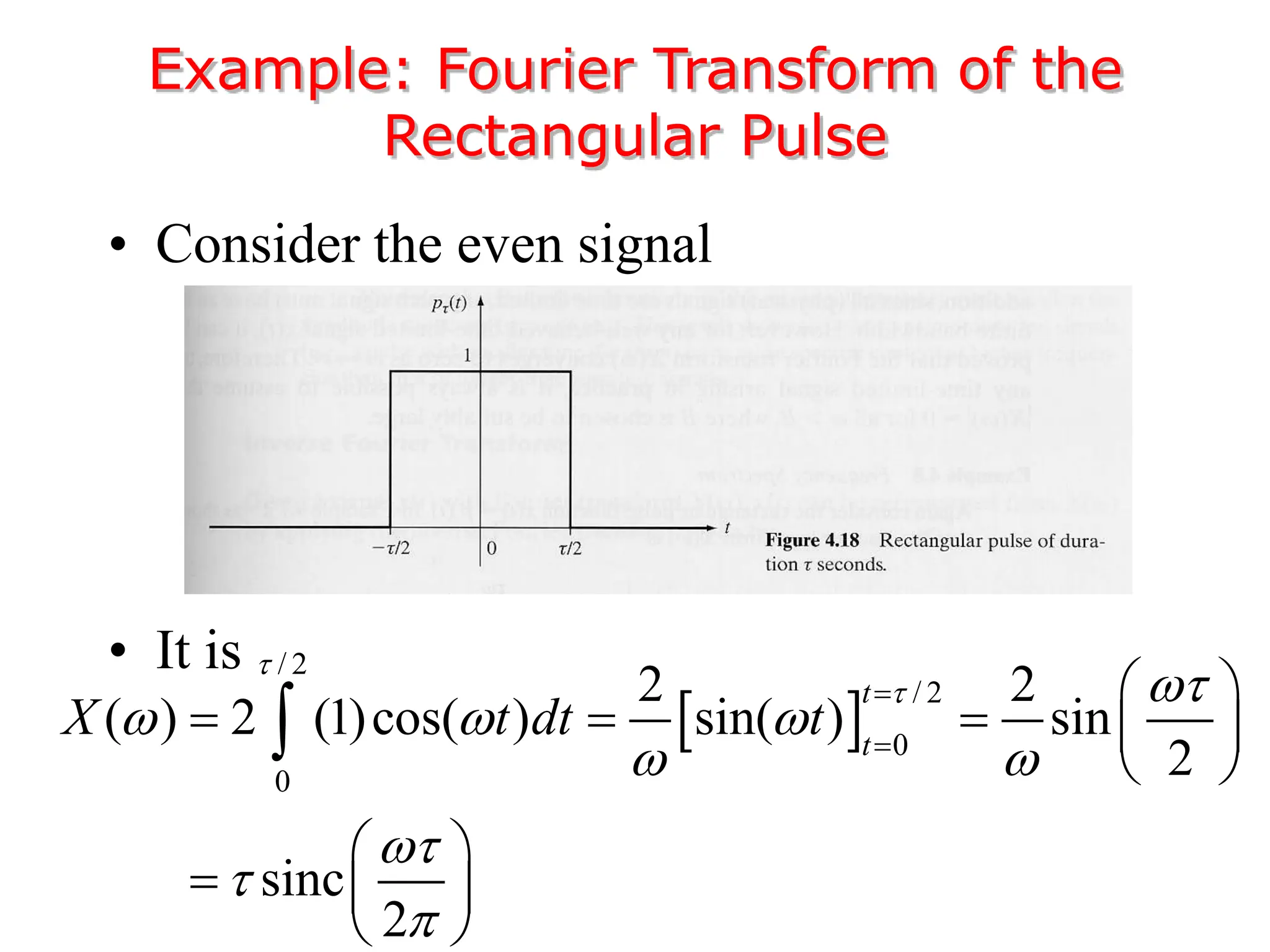
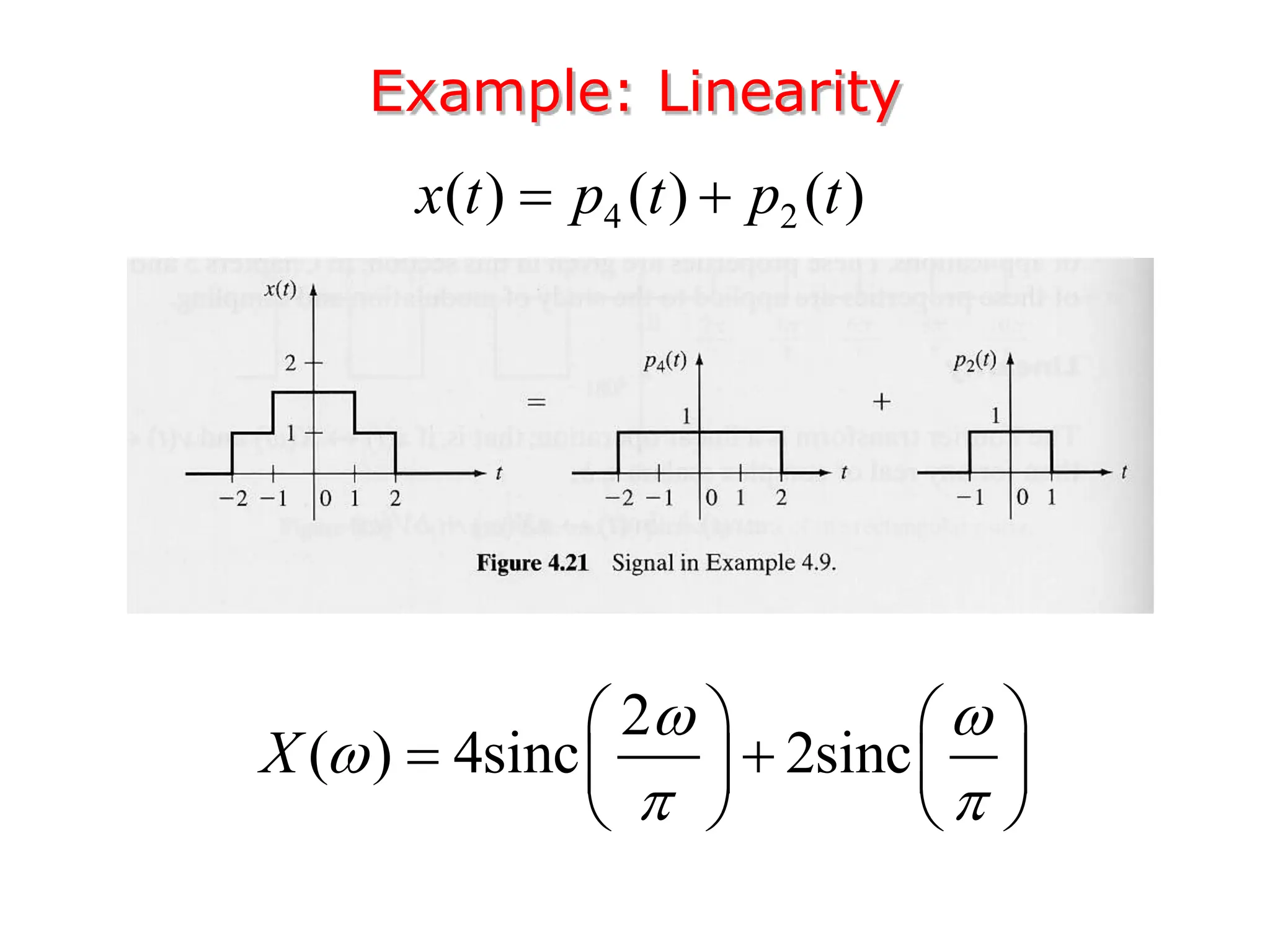
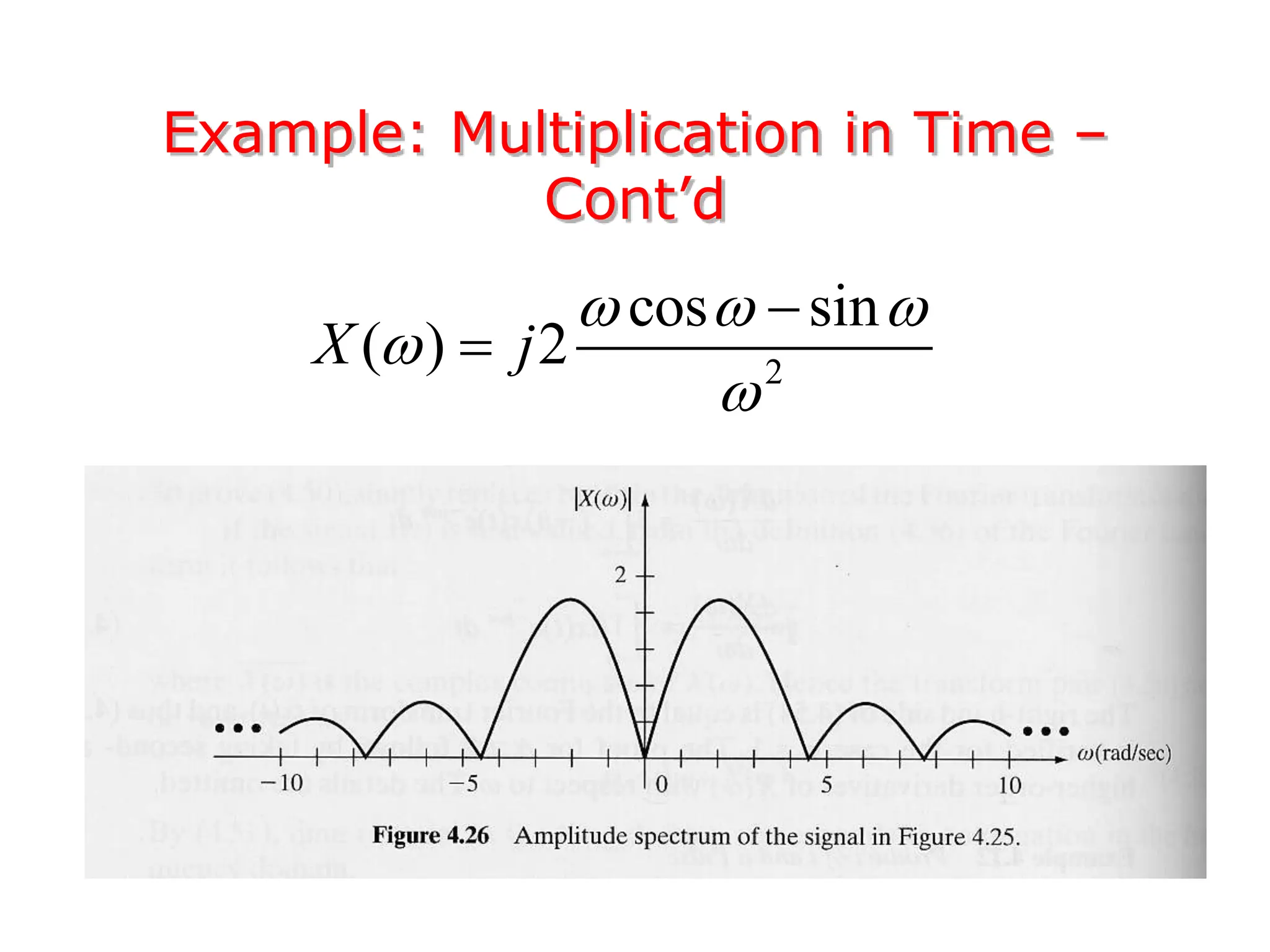
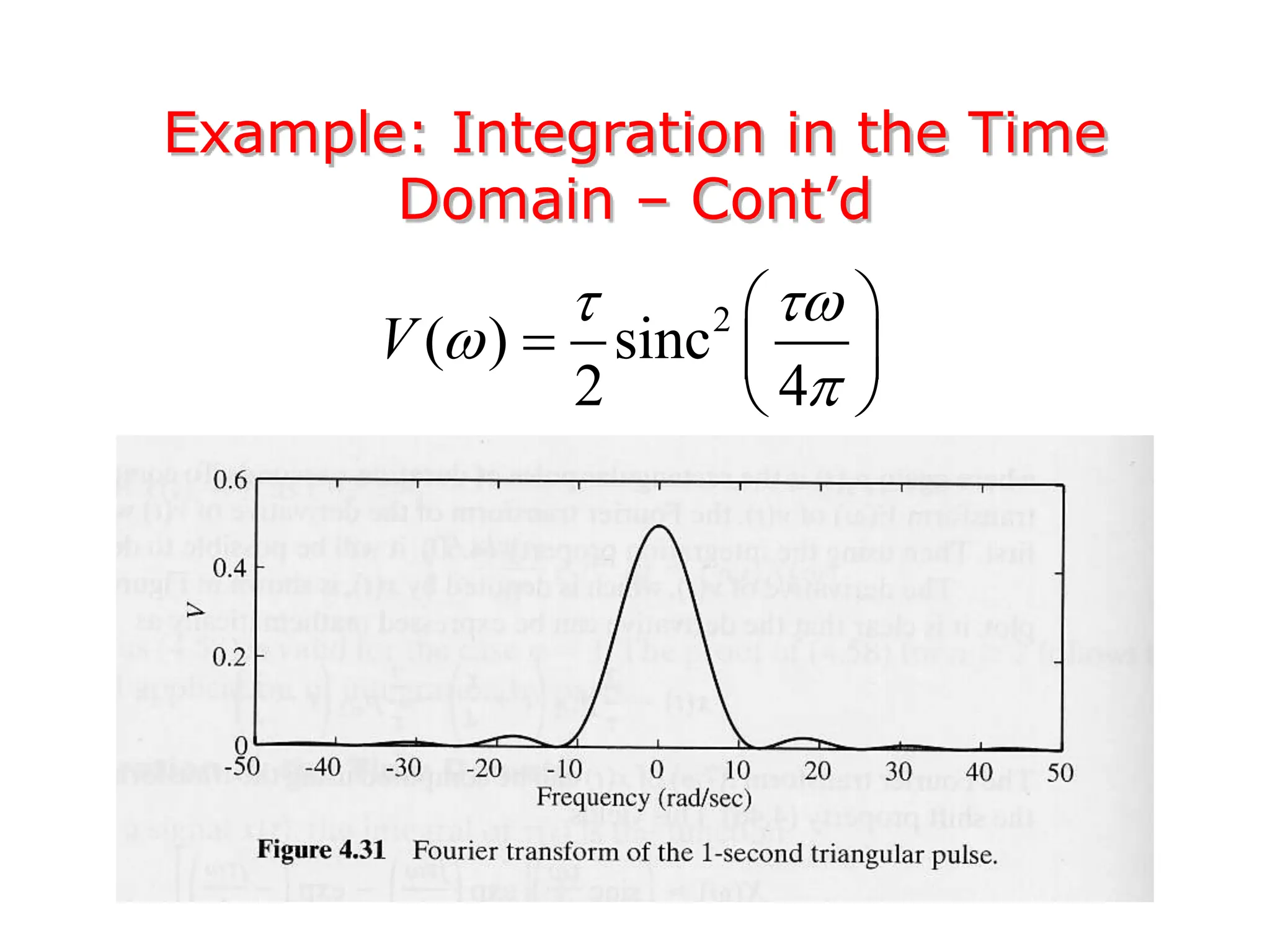
1. The document discusses Fourier analysis techniques for representing signals, including Fourier series and the Fourier transform. It uses the example of a rectangular pulse train to illustrate these concepts. 2. A periodic signal like a rectangular pulse train can be represented by a Fourier series as a sum of sinusoids with frequencies that are integer multiples of the fundamental frequency. 3. The Fourier transform allows representing aperiodic signals as a sum of sinusoids of all possible frequencies, resulting in a continuous spectrum rather than a discrete line spectrum. The Fourier transform of a rectangular pulse is a sinc function.

1. Chapter 4
The Fourier Series and
Fourier Transform

2. • Consider the CT signal defined by
• The frequencies `present in the signal’ are the
frequency of the component sinusoids
• The signal x(t) is completely characterized by
the set of frequencies , the set of amplitudes
, and the set of phases
Representation of Signals in Terms
of Frequency Components
1
( ) cos( ),
N
k k k
k
x t A t t
 

  

k

k

k
A k


3. • Consider the CT signal given by
• The signal has only three frequency
components at 1,4, and 8 rad/sec, amplitudes
and phases
• The shape of the signal x(t) depends on the
relative magnitudes of the frequency
components, specified in terms of the
amplitudes
Example: Sum of Sinusoids
1 2 3
( ) cos( ) cos(4 /3) cos(8 / 2),
x t A t A t A t
t
 
    

1 2 3
, ,
A A A 0, /3, / 2
 
1 2 3
, ,
A A A

4. Example: Sum of Sinusoids –Cont’d
1
2
3
0.5
1
0
A
A
A





 

1
2
3
1
0.5
0
A
A
A





 

1
2
3
1
1
0
A
A
A





 


5. Example: Sum of Sinusoids –Cont’d
1
2
3
0.5
1
0.5
A
A
A





 

1
2
3
1
0.5
0.5
A
A
A





 

1
2
3
1
1
1
A
A
A





 


6. • Plot of the amplitudes of the sinusoids
making up x(t) vs.
• Example:
Amplitude Spectrum
k
A



7. • Plot of the phases of the sinusoids
making up x(t) vs.
• Example:
Phase Spectrum
k




8. • Euler formula:
• Thus
whence
Complex Exponential Form
cos( ) sin( )
j
e j

 
 
( )
cos( ) k k
j t
k k k k
A t A e  
  
 
   
( )
1
( ) ,
k k
N
j t
k
k
x t A e t
 


 
  
 

real part

9. • And, recalling that where
, we can also write
• This signal contains both positive and
negative frequencies
• The negative frequencies stem from
writing the cosine in terms of complex
exponentials and have no physical meaning
Complex Exponential Form – Cont’d
( ) ( )/ 2
z z z
  
z a jb
 
( ) ( )
1
1
( ) ,
2
k k k k
N
j t j t
k k
k
x t A e A e t
   
  

 
  
 

k



10. • By defining
it is also
Complex Exponential Form – Cont’d
2
k
j
k
k
A
c e 

2
k
j
k
k
A
c e 

 
1
0
( ) ,
k k k
N N
j t j t j t
k k k
k N
k
k
x t c e c e c e t
  





 
   
 
 
complex exponential form
of the signal x(t)

11. • The amplitude spectrum of x(t) is defined as
the plot of the magnitudes versus
• The phase spectrum of x(t) is defined as the
plot of the angles versus
• This results in line spectra which are defined
for both positive and negative frequencies
• Notice: for
Line Spectra
| |
k
c


arg( )
k k
c c
 
| | | |
k k
c c
 k k
c c
  
arg( ) arg( )
k k
c c
 
1,2,
k 

12. Example: Line Spectra
( ) cos( ) 0.5cos(4 /3) cos(8 / 2)
x t t t t
 
    
0.
0.

13. • Let x(t) be a CT periodic signal with period
T, i.e.,
• Example: the rectangular pulse train
Fourier Series Representation of
Periodic Signals
( ) ( ),
x t T x t t R
   

14. • Then, x(t) can be expressed as
where is the fundamental
frequency (rad/sec) of the signal and
The Fourier Series
0
( ) ,
jk t
k
k
x t c e t



 

/ 2
/ 2
1
( ) , 0, 1, 2,
o
T
jk t
k
T
c x t e dt k
T



   

0 2 /T
 

is called the constant or dc component of x(t)
0
c

15. • The frequencies present in x(t) are
integer multiples of the fundamental
frequency
• Notice that, if the dc term is added to
and we set , the Fourier series is a
special case of the above equation where all
the frequencies are integer multiples of
The Fourier Series – Cont’d
0
k
0

0
( ) k
N
j t
k
k N
k
x t c e 


 
N  
0

0
c

16. • A periodic signal x(t), has a Fourier series
if it satisfies the following conditions:
1. x(t) is absolutely integrable over any
period, namely
2. x(t) has only a finite number of maxima
and minima over any period
3. x(t) has only a finite number of
discontinuities over any period
Dirichlet Conditions
| ( ) | ,
a T
a
x t dt a

   


17. • From figure, whence
• Clearly x(t) satisfies the Dirichlet conditions and
thus has a Fourier series representation
Example: The Rectangular Pulse Train
2
T  0 2 / 2
  
 

18. Example: The Rectangular Pulse
Train – Cont’d
|( 1)/ 2|
1 1
( ) ( 1) ,
2
k jk t
k
k odd
x t e t
k





   


19. • By using Euler’s formula, we can rewrite
as
• This expression is called the trigonometric
Fourier series of x(t)
Trigonometric Fourier Series
0
( ) ,
jk t
k
k
x t c e t



 

0 0
1
( ) 2 | |cos( ),
k k
k
x t c c k t c t



    

dc component k-th harmonic

20. • The expression
can be rewritten as
Example: Trigonometric Fourier
Series of the Rectangular Pulse Train
|( 1)/ 2|
1 1
( ) ( 1) ,
2
k jk t
k
k odd
x t e t
k





   

( 1)/ 2
1
1 2
( ) cos ( 1) 1 ,
2 2
k
k
k odd
x t k t t
k






 
 
     
 
 
 


21. • Given an odd positive integer N, define the
N-th partial sum of the previous series
• According to Fourier’s theorem, it should be
Gibbs Phenomenon
( 1)/ 2
1
1 2
( ) cos ( 1) 1 ,
2 2
N
k
N
k
k odd
x t k t t
k





 
 
     
 
 
 

lim | ( ) ( ) | 0
N
N
x t x t

 

22. Gibbs Phenomenon – Cont’d
3 ( )
x t 9 ( )
x t

23. Gibbs Phenomenon – Cont’d
21( )
x t 45 ( )
x t
overshoot: about 9 % of the signal magnitude
(present even if )
N  

24. • Let x(t) be a periodic signal with period T
• The average power P of the signal is defined
as
• Expressing the signal as
it is also
Parseval’s Theorem
/ 2
2
/ 2
1
( )
T
T
P x t dt
T 
 
0
( ) ,
jk t
k
k
x t c e t



 

2
| |
k
k
P c


 

25. • We have seen that periodic signals can be
represented with the Fourier series
• Can aperiodic signals be analyzed in terms of
frequency components?
• Yes, and the Fourier transform provides the
tool for this analysis
• The major difference w.r.t. the line spectra of
periodic signals is that the spectra of
aperiodic signals are defined for all real
values of the frequency variable not just
for a discrete set of values
Fourier Transform


26. Frequency Content of the
Rectangular Pulse
( )
T
x t
( )
x t
( ) lim ( )
T
T
x t x t



27. • Since is periodic with period T, we can
write
Frequency Content of the
Rectangular Pulse – Cont’d
( )
T
x t
0
( ) ,
jk t
T k
k
x t c e t



 

where
/ 2
/ 2
1
( ) , 0, 1, 2,
o
T
jk t
k
T
c x t e dt k
T



   


28. • What happens to the frequency components
of as ?
• For
• For
Frequency Content of the
Rectangular Pulse – Cont’d
( )
T
x t T  
0
k 
0
1
c
T

0
k 
0 0
0
2 1
sin sin , 1, 2,
2 2
k
k k
c k
k T k
 
 
   
    
   
   
0 2 /T
 


29. Frequency Content of the
Rectangular Pulse – Cont’d
plots of
vs.
for
| |
k
T c
0
k
 

2,5,10
T 

30. • It can be easily shown that
where
Frequency Content of the
Rectangular Pulse – Cont’d
lim sinc ,
2
k
T
Tc




 
 
 
 
sin( )
sinc( )




31. • The Fourier transform of the rectangular
pulse x(t) is defined to be the limit of
as , i.e.,
Fourier Transform of the Rectangular
Pulse
( ) lim sinc ,
2
k
T
X Tc

 


 
  
 
 
k
Tc
T  
| ( ) |
X  arg( ( ))
X 

32. • The Fourier transform of the
rectangular pulse x(t) can be expressed in
terms of x(t) as follows:
Fourier Transform of the Rectangular
Pulse – Cont’d
( )
X 
1
( ) , 0, 1, 2,
o
jk t
k
c x t e dt k
T




   

( ) , 0, 1, 2,
o
jk t
k
Tc x t e dt k




   

whence
( ) 0 for / 2 and / 2
x t t T t T
   

33. • Now, by definition and,
since
• The inverse Fourier transform of is
Fourier Transform of the Rectangular
Pulse – Cont’d
( ) lim k
T
X Tc



0 as
k T
 
  
( ) ( ) ,
j t
X x t e dt

 



 

1
( ) ( ) ,
2
j t
x t X e d t

 



 

( )
X 

34. • Given a signal x(t), its Fourier transform
is defined as
• A signal x(t) is said to have a Fourier
transform in the ordinary sense if the above
integral converges
The Fourier Transform in the General
Case
( )
X 
( ) ( ) ,
j t
X x t e dt

 



 


35. • The integral does converge if
1. the signal x(t) is “well-behaved”
2. and x(t) is absolutely integrable, namely,
• Note: well behaved means that the signal
has a finite number of discontinuities,
maxima, and minima within any finite time
interval
The Fourier Transform in the General
Case – Cont’d
| ( ) |
x t dt


 


36. • Consider the signal
• Clearly x(t) does not satisfy the first
requirement since
• Therefore, the constant signal does not have
a Fourier transform in the ordinary sense
• Later on, we’ll see that it has however a
Fourier transform in a generalized sense
Example: The DC or Constant Signal
( ) 1,
x t t
 
| ( ) |
x t dt dt
 
 
 
 

37. • Consider the signal
• Its Fourier transform is given by
Example: The Exponential Signal
( ) ( ),
bt
x T e u t b

 
( ) ( )
0 0
( ) ( )
1
bt j t
t
b j t b j t
t
X e u t e dt
e dt e
b j

 



 



   


 
    




38. • If , does not exist
• If , and does not
exist either in the ordinary sense
• If , it is
Example: The Exponential Signal –
Cont’d
0
b  ( )
X 
0
b  ( ) ( )
x t u t
 ( )
X 
0
b 
1
( )
X
b j




2 2
1
| ( ) |
X
b




amplitude spectrum
arg( ( )) arctan
X
b


 
   
 
phase spectrum

39. Example: Amplitude and Phase
Spectra of the Exponential Signal
10
( ) ( )
t
x t e u t



40. • Consider
• Since in general is a complex
function, by using Euler’s formula
Rectangular Form of the Fourier
Transform
( ) ( ) ,
j t
X x t e dt

 



 

( )
X 
( ) ( )
( ) ( )cos( ) ( )sin( )
R I
X x t t dt j x t t dt
 
  
 
 
 
  
 
 
 
( ) ( ) ( )
X R jI
  
 

41. • can be expressed in
a polar form as
where
Polar Form of the Fourier Transform
( ) | ( ) | exp( arg( ( )))
X X j X
  

( ) ( ) ( )
X R jI
  
 
2 2
| ( ) | ( ) ( )
X R I
  
 
( )
arg( ( )) arctan
( )
I
X
R



 
  
 

42. • If x(t) is real-valued, it is
• Moreover
whence
Fourier Transform of
Real-Valued Signals
( ) ( )
X X
 

 
( ) | ( ) | exp( arg( ( )))
X X j X
  

 
| ( ) | | ( ) | and
arg( ( )) arg( ( ))
X X
X X
 
 
 
  
Hermitian
symmetry

43. • Even signal:
• Odd signal:
Fourier Transforms of
Signals with Even or Odd Symmetry
( ) ( )
x t x t
 
0
( ) 2 ( )cos( )
X x t t dt
 

 
( ) ( )
x t x t
  
0
( ) 2 ( )sin( )
X j x t t dt
 

  

44. • Consider the even signal
• It is
Example: Fourier Transform of the
Rectangular Pulse
 
/ 2
/ 2
0
0
2 2
( ) 2 (1)cos( ) sin( ) sin
2
sinc
2
t
t
X t dt t

 
  
 





 
    
 
 
  
 


45. Example: Fourier Transform of the
Rectangular Pulse – Cont’d
( ) sinc
2
X

 

 
  
 

46. Example: Fourier Transform of the
Rectangular Pulse – Cont’d
amplitude
spectrum
phase
spectrum

47. • A signal x(t) is said to be bandlimited if its
Fourier transform is zero for all
where B is some positive number, called
the bandwidth of the signal
• It turns out that any bandlimited signal must
have an infinite duration in time, i.e.,
bandlimited signals cannot be time limited
Bandlimited Signals
( )
X  B
 

48. • If a signal x(t) is not bandlimited, it is said
to have infinite bandwidth or an infinite
spectrum
• Time-limited signals cannot be
bandlimited and thus all time-limited
signals have infinite bandwidth
• However, for any well-behaved signal x(t)
it can be proven that
whence it can be assumed that
Bandlimited Signals – Cont’d
lim ( ) 0
X




| ( ) | 0
X B
 
  
B being a convenient large number

49. • Given a signal x(t) with Fourier transform
, x(t) can be recomputed from
by applying the inverse Fourier transform
given by
• Transform pair
Inverse Fourier Transform
( )
X  ( )
X 
1
( ) ( ) ,
2
j t
x t X e d t

 



 

( ) ( )
x t X 


50. Properties of the Fourier Transform
• Linearity:
• Left or Right Shift in Time:
• Time Scaling:
( ) ( )
x t X 
 ( ) ( )
y t Y 

( ) ( ) ( ) ( )
x t y t X Y
     
  
0
0
( ) ( ) j t
x t t X e 
 
 
1
( )
x at X
a a

 
  
 

51. Properties of the Fourier Transform
• Time Reversal:
• Multiplication by a Power of t:
• Multiplication by a Complex Exponential:
( ) ( )
x t X 
  
( ) ( ) ( )
n
n n
n
d
t x t j X
d



0
0
( ) ( )
j t
x t e X

 
 

52. Properties of the Fourier Transform
• Multiplication by a Sinusoid (Modulation):
• Differentiation in the Time Domain:
 
0 0 0
( )sin( ) ( ) ( )
2
j
x t t X X
    
   
 
0 0 0
1
( )cos( ) ( ) ( )
2
x t t X X
    
   
( ) ( ) ( )
n
n
n
d
x t j X
dt
 


53. Properties of the Fourier Transform
• Integration in the Time Domain:
• Convolution in the Time Domain:
• Multiplication in the Time Domain:
1
( ) ( ) (0) ( )
t
x d X X
j
     


 

( ) ( ) ( ) ( )
x t y t X Y
 
 
( ) ( ) ( ) ( )
x t y t X Y
 
 

54. Properties of the Fourier Transform
• Parseval’s Theorem:
• Duality:
1
( ) ( ) ( ) ( )
2
x t y t dt X Y d
  



 
2 2
1
| ( ) | | ( ) |
2
x t dt X d
 


 
( ) ( )
y t x t

if
( ) 2 ( )
X t x
 
 

55. Properties of the Fourier Transform -
Summary

56. Example: Linearity
4 2
( ) ( ) ( )
x t p t p t
 
2
( ) 4sinc 2sinc
X
 

 
   
 
   
   

57. Example: Time Shift
2
( ) ( 1)
x t p t
 
( ) 2sinc j
X e 




 
  
 

58. Example: Time Scaling
2 ( )
p t
2 (2 )
p t
2sinc


 
 
 
sinc
2


 
 
 
time compression frequency expansion

time expansion frequency compression

1
a 
0 1
a
 

59. Example: Multiplication in Time
2
( ) ( )
x t tp t

2
sin cos sin
( ) 2sinc 2 2
d d
X j j j
d d
    

    
  
   
  
   
 
   
 

60. Example: Multiplication in Time –
Cont’d
2
cos sin
( ) 2
X j
  





61. Example: Multiplication by a Sinusoid
0
( ) ( )cos( )
x t p t t
 
 sinusoidal
burst
0 0
1 ( ) ( )
( ) sinc sinc
2 2 2
X
     
  
 
 
 
   
 
   
 
   
 

62. Example: Multiplication by a
Sinusoid – Cont’d
0 0
1 ( ) ( )
( ) sinc sinc
2 2 2
X
     
  
 
 
 
   
 
   
 
   
 
0 60 /sec
0.5
rad








63. Example: Integration in the Time
Domain
2 | |
( ) 1 ( )
t
v t p t


 
 
 
 
( )
( )
dv t
x t
dt


64. Example: Integration in the Time
Domain – Cont’d
• The Fourier transform of x(t) can be easily
found to be
• Now, by using the integration property, it is
( ) sinc 2sin
4 4
X j
 


  
   
    
  
   
  
2
1
( ) ( ) (0) ( ) sinc
2 4
V X X
j
 
    
 
 
    
 

65. Example: Integration in the Time
Domain – Cont’d
2
( ) sinc
2 4
V
 


 
  
 

66. • Fourier transform of
• Applying the duality property
Generalized Fourier Transform
( )
t

( ) 1
j t
t e dt

 

 ( ) 1
t
 

( ) 1, 2 ( )
x t t  
  
generalized Fourier transform
of the constant signal ( ) 1,
x t t
 

67. Generalized Fourier Transform of
Sinusoidal Signals
 
0 0 0
cos( ) ( ) ( )
t
       
   
 
0 0 0
sin( ) ( ) ( )
t j
       
   

68. Fourier Transform of Periodic Signals
• Let x(t) be a periodic signal with period T;
as such, it can be represented with its
Fourier transform
• Since , it is
0
0
2 ( )
j t
e 
  
 
0
( ) jk t
k
k
x t c e 


  0 2 /T
 

0
( ) 2 ( )
k
k
X c k
    


 


69. • Since
using the integration property, it is
Fourier Transform of
the Unit-Step Function
( ) ( )
t
u t d
  

 
1
( ) ( ) ( )
t
u t d
j
    


  


70. Common Fourier Transform Pairs