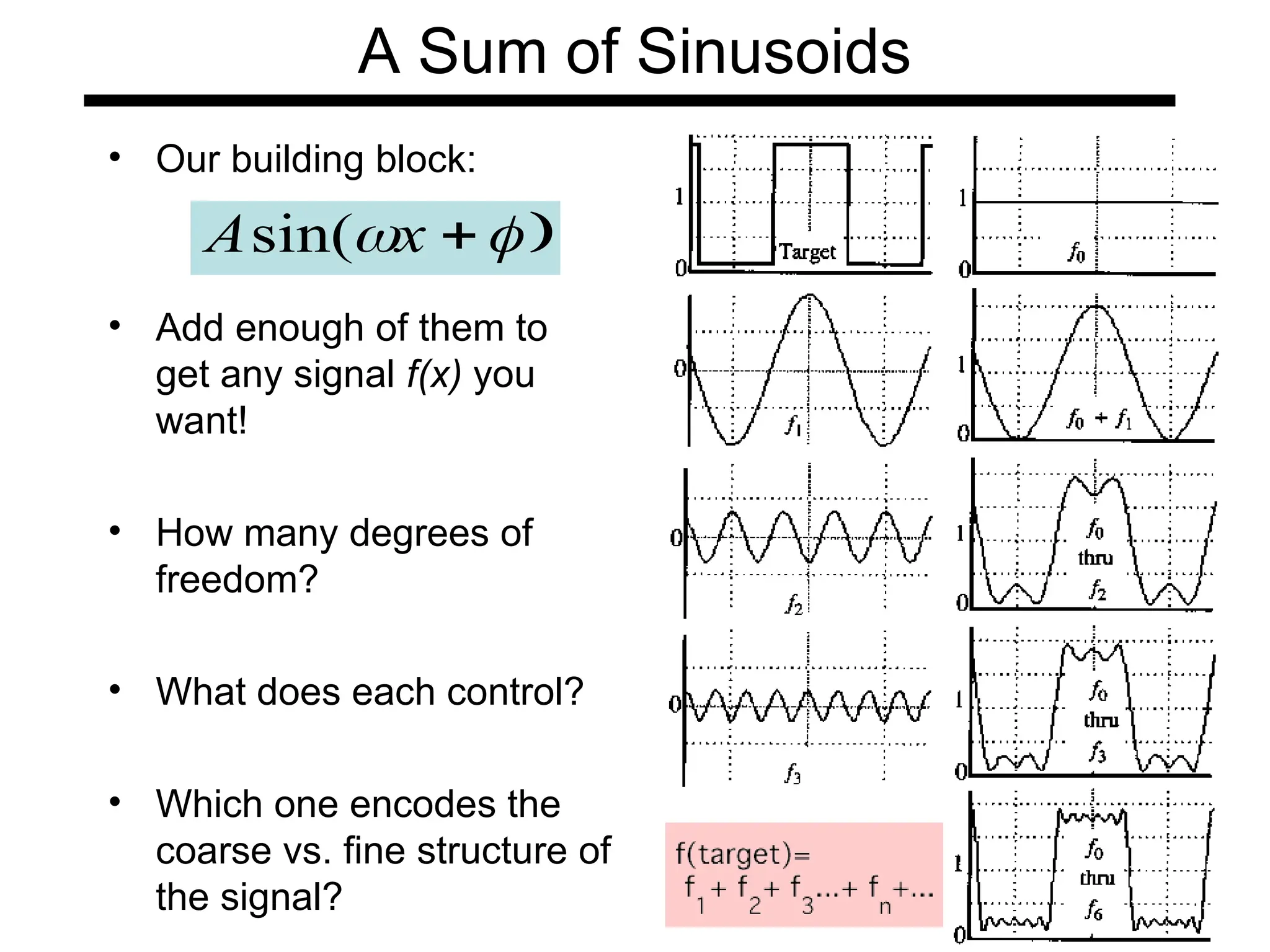
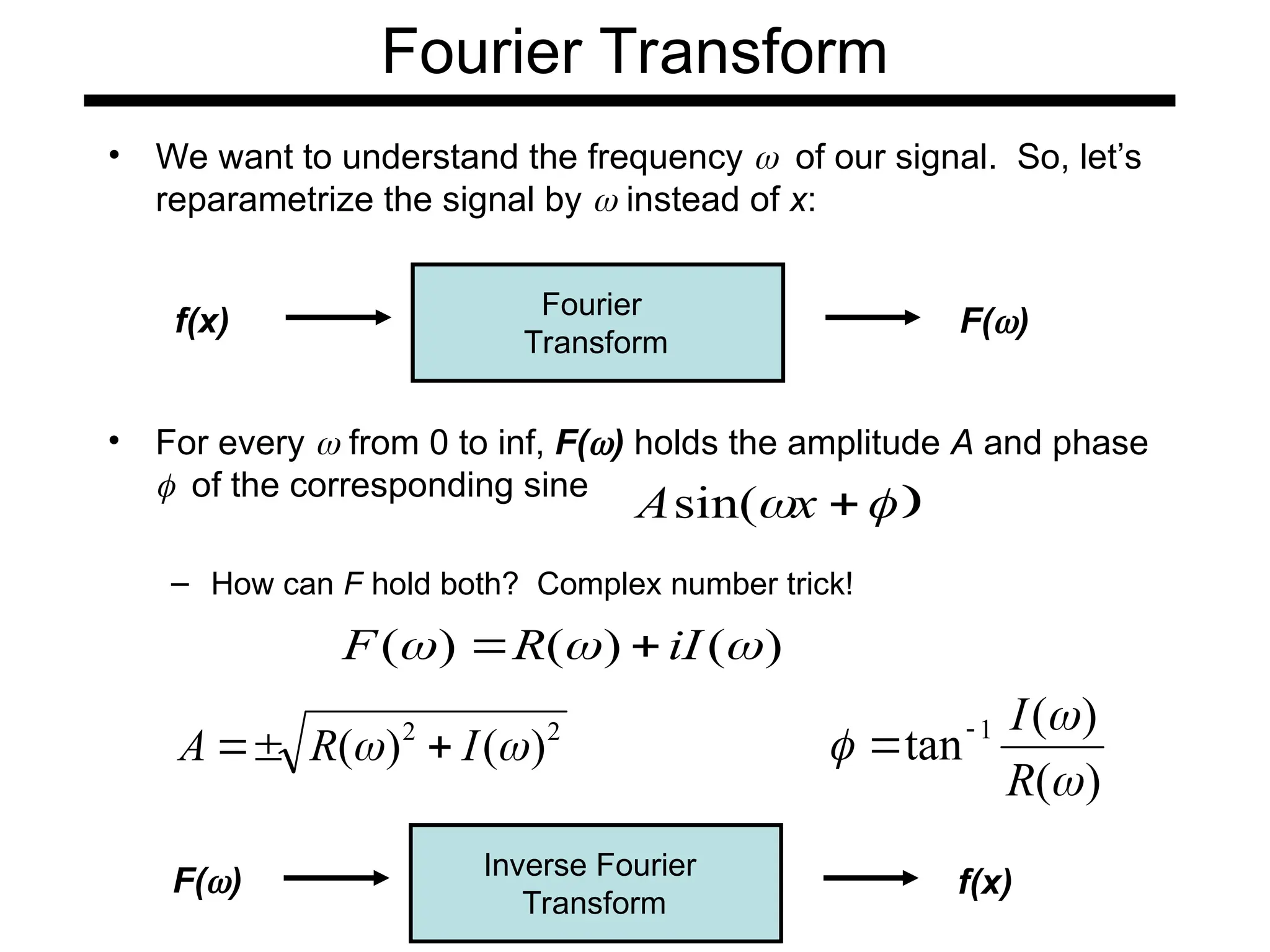
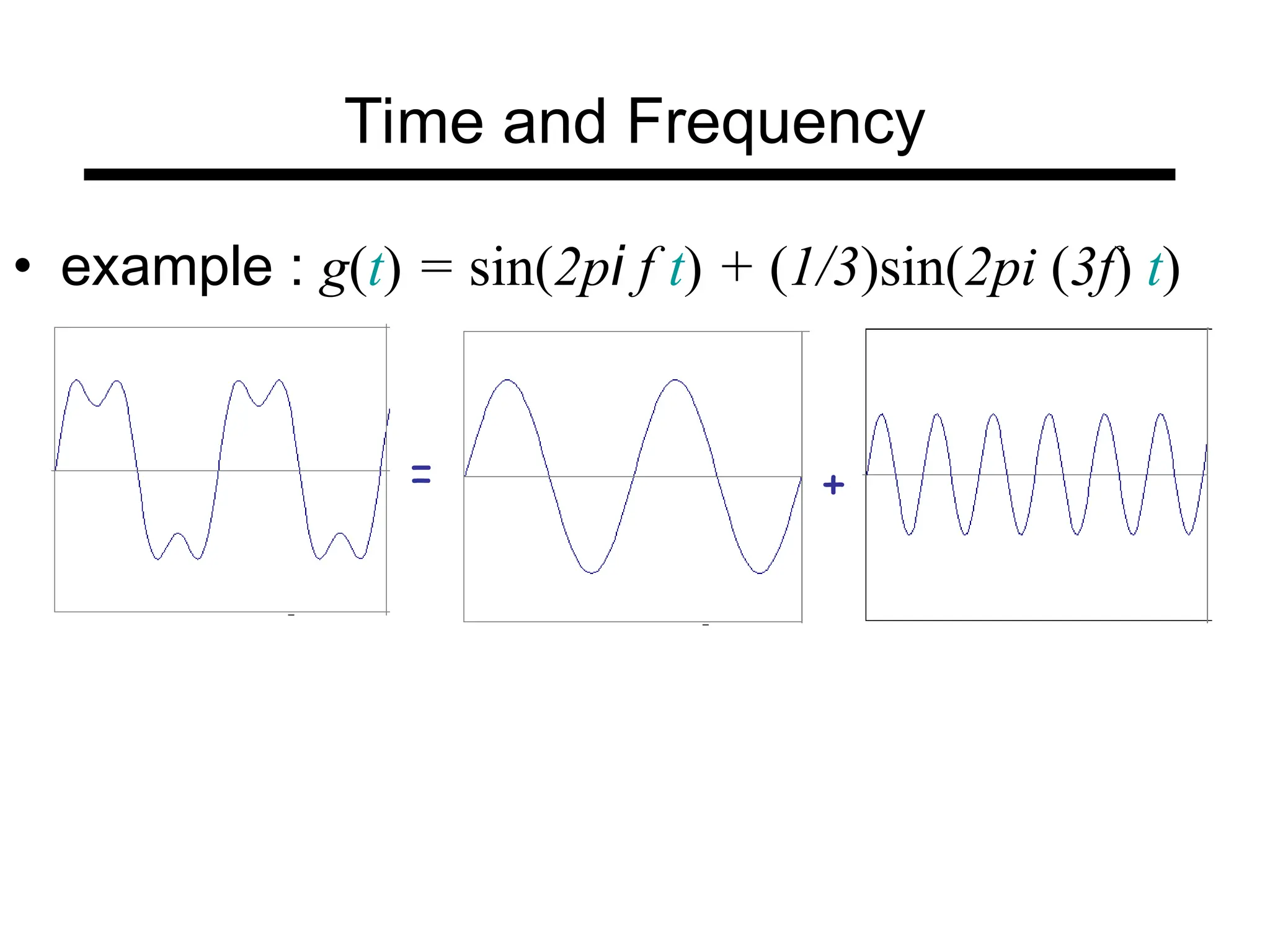
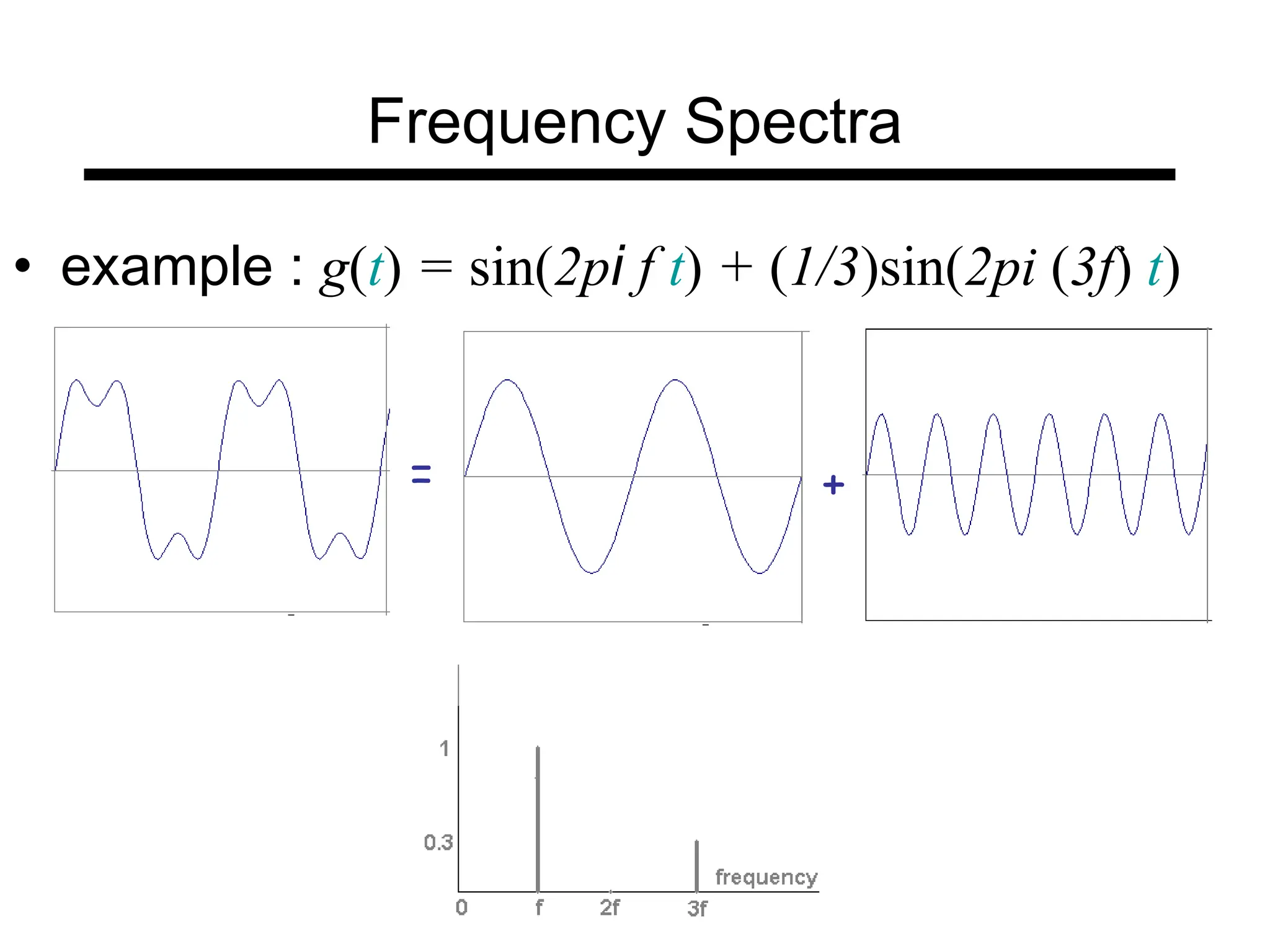
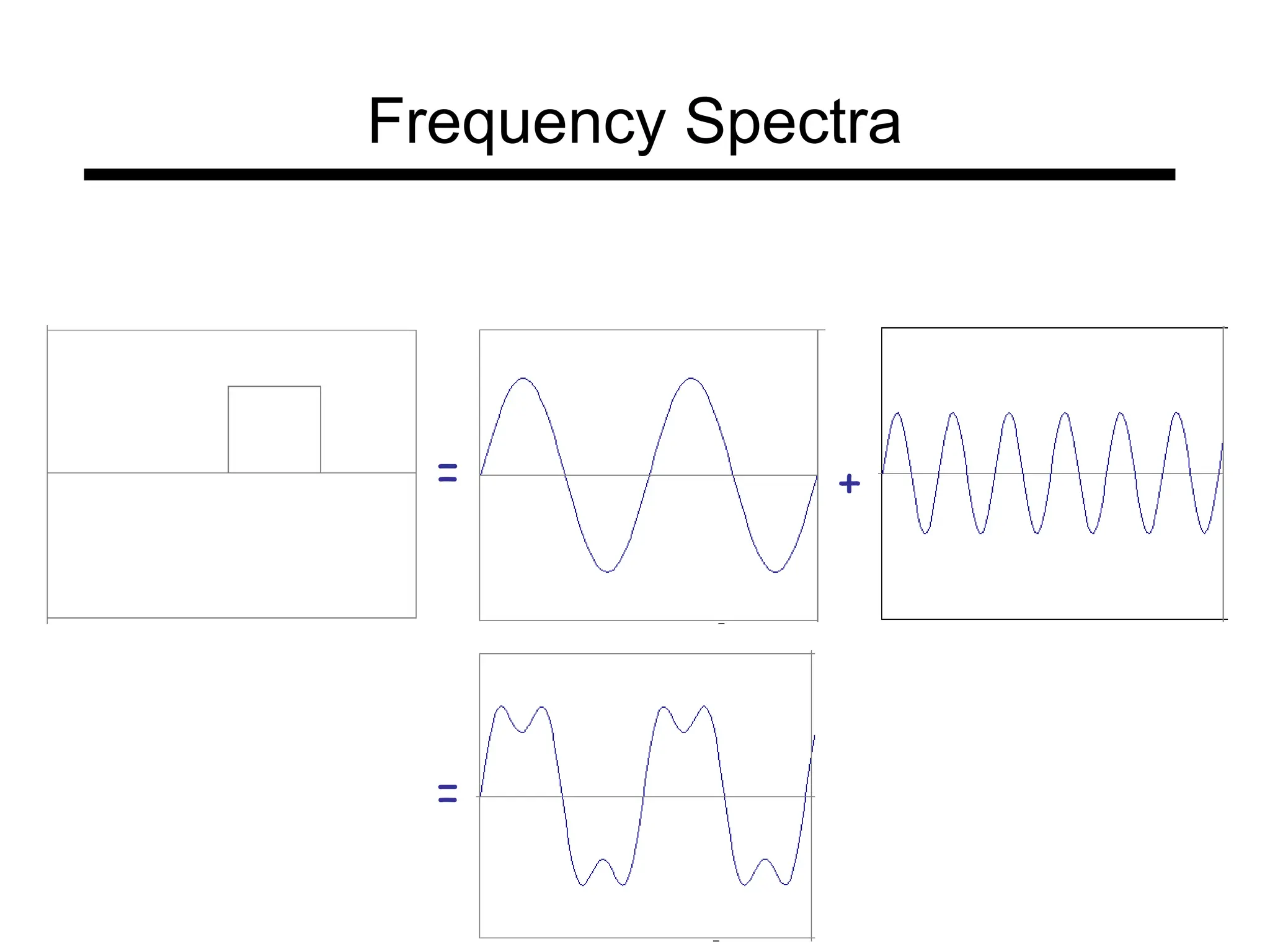
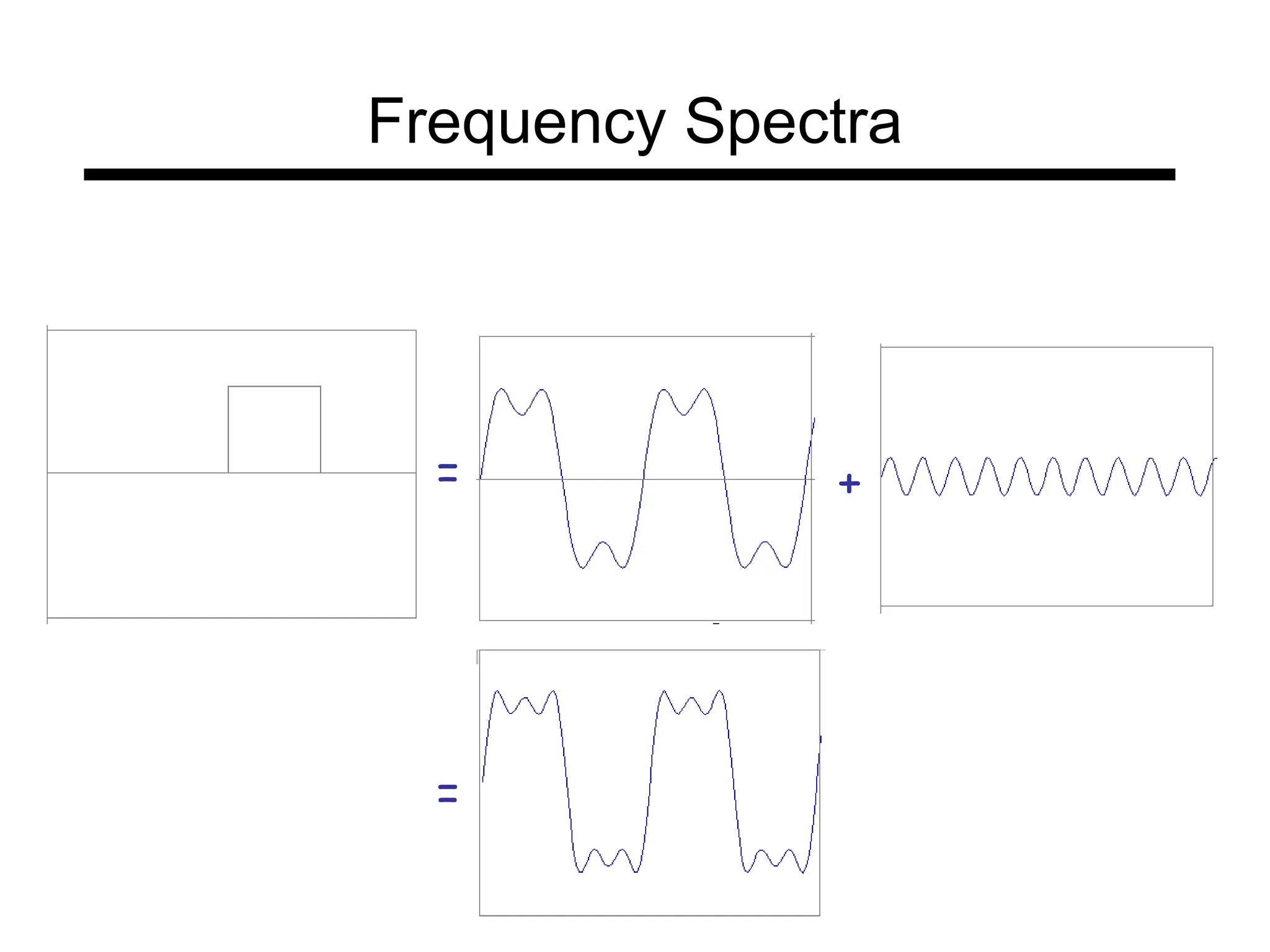
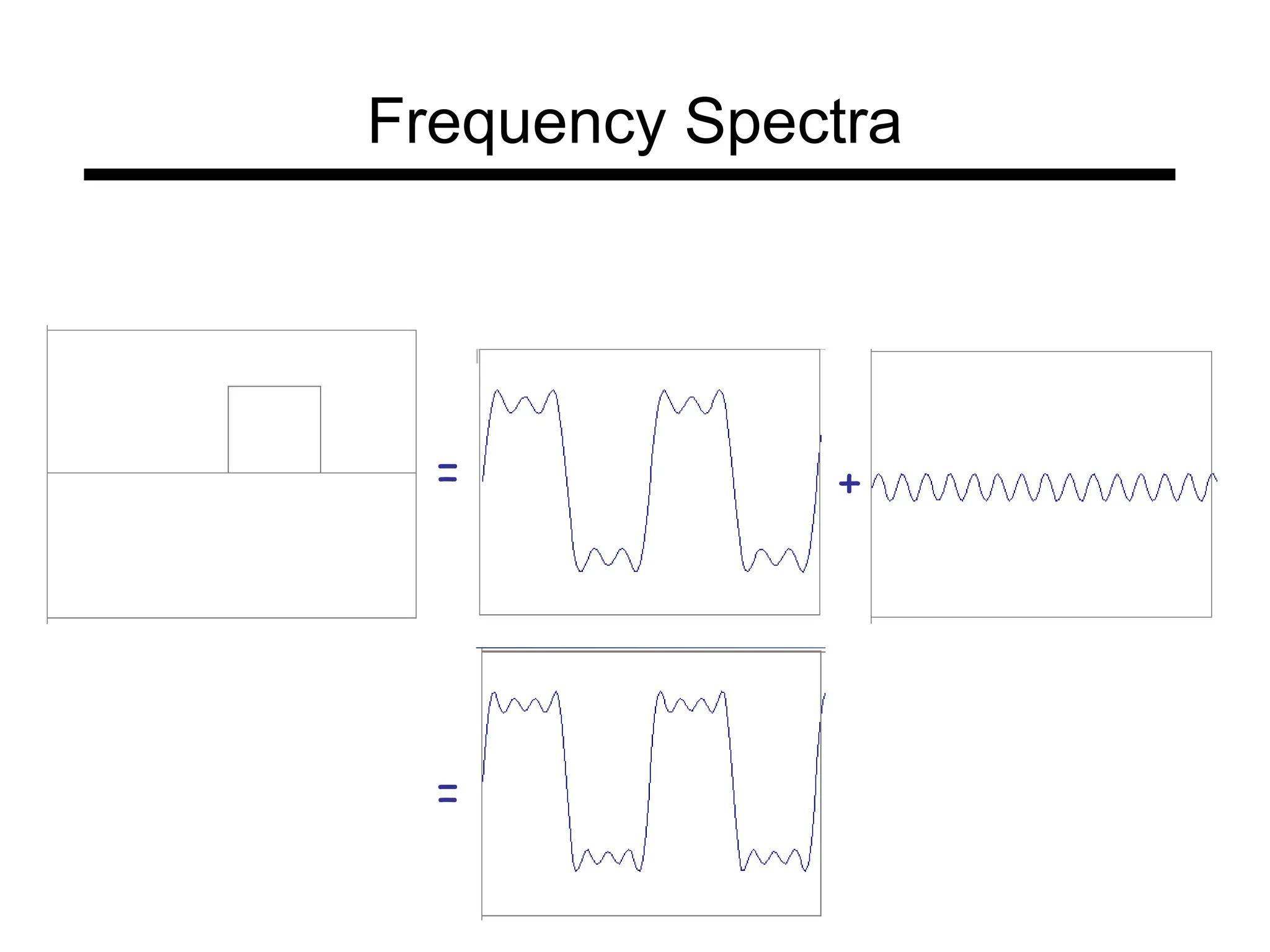
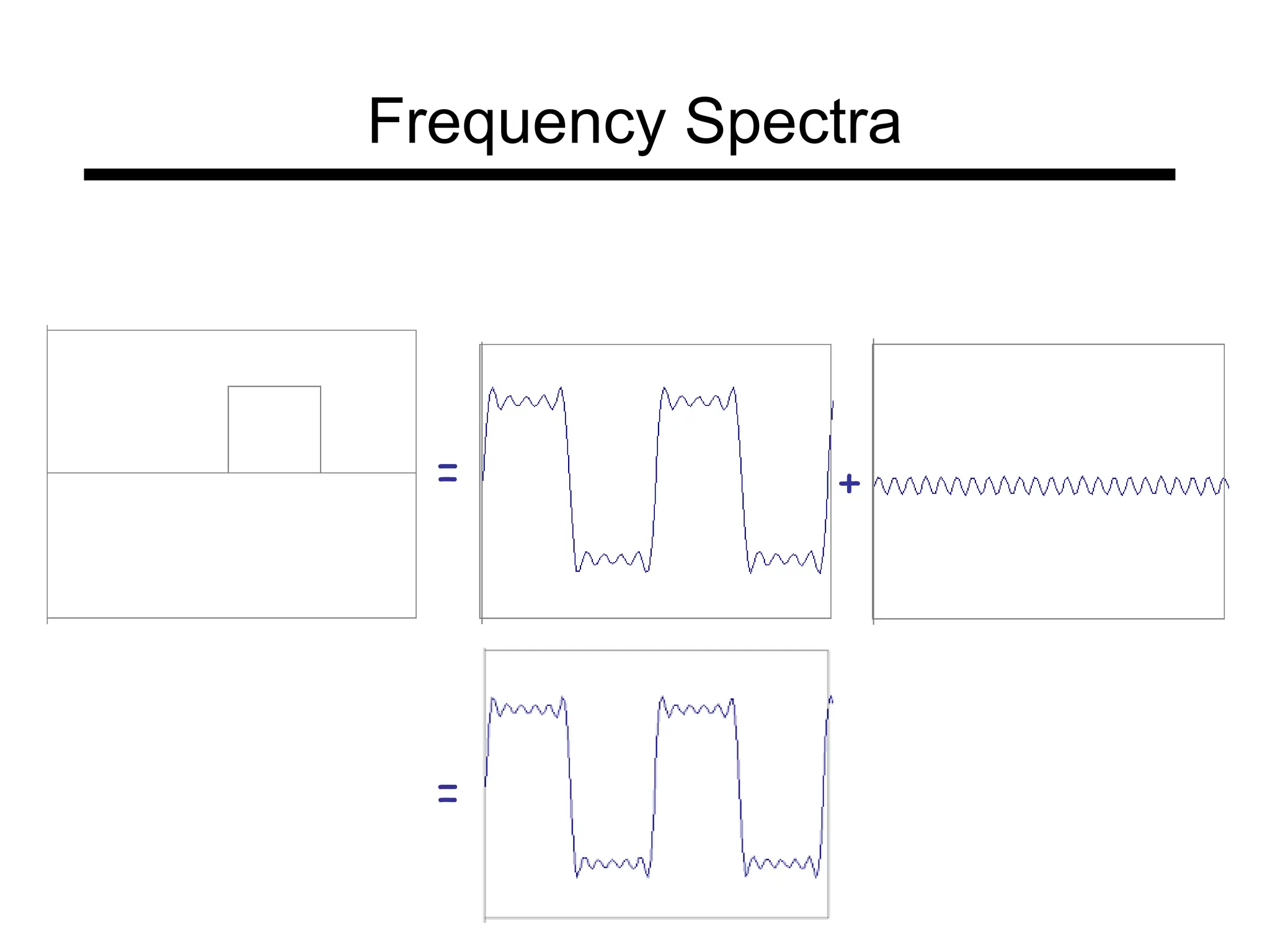
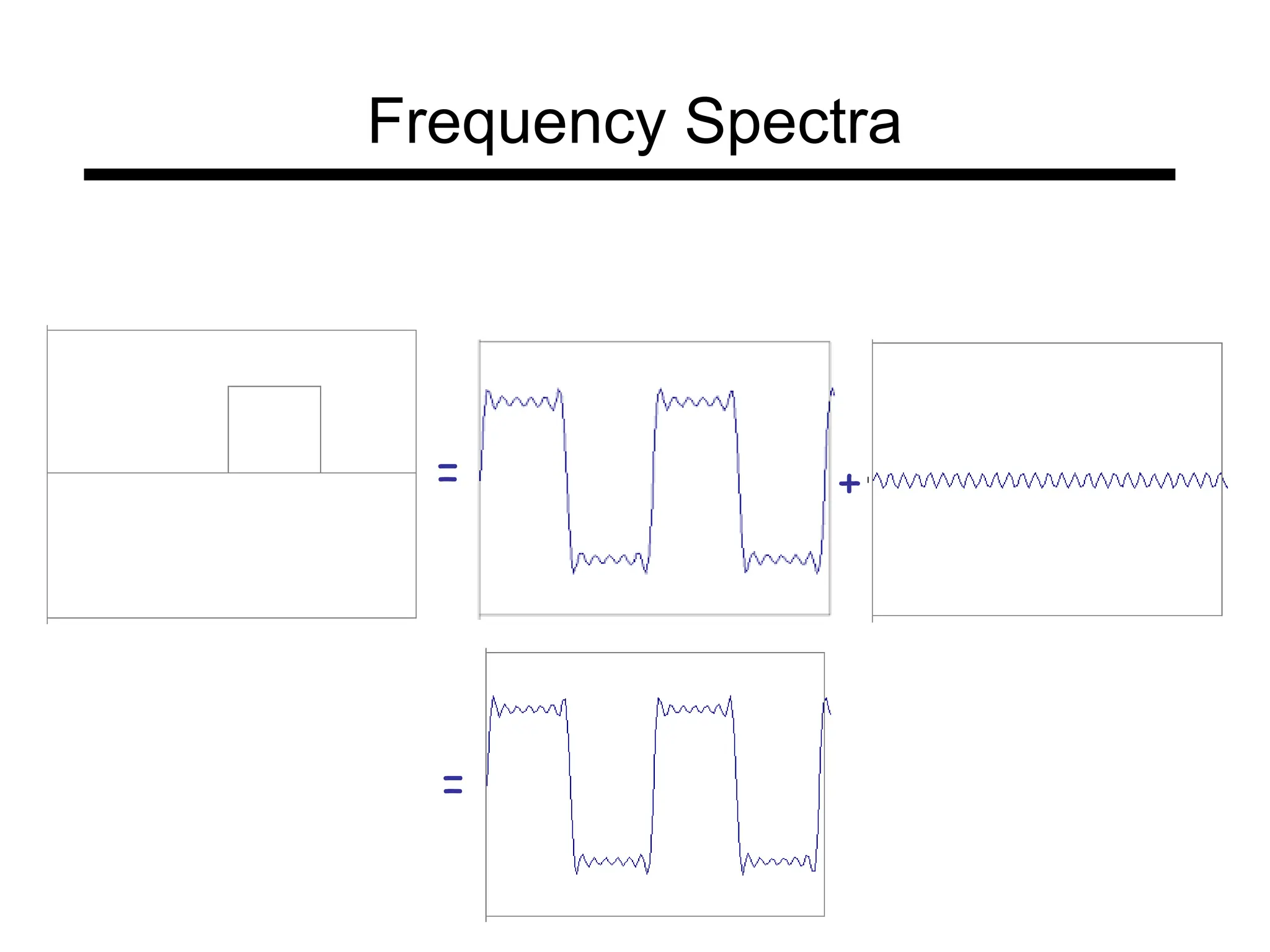
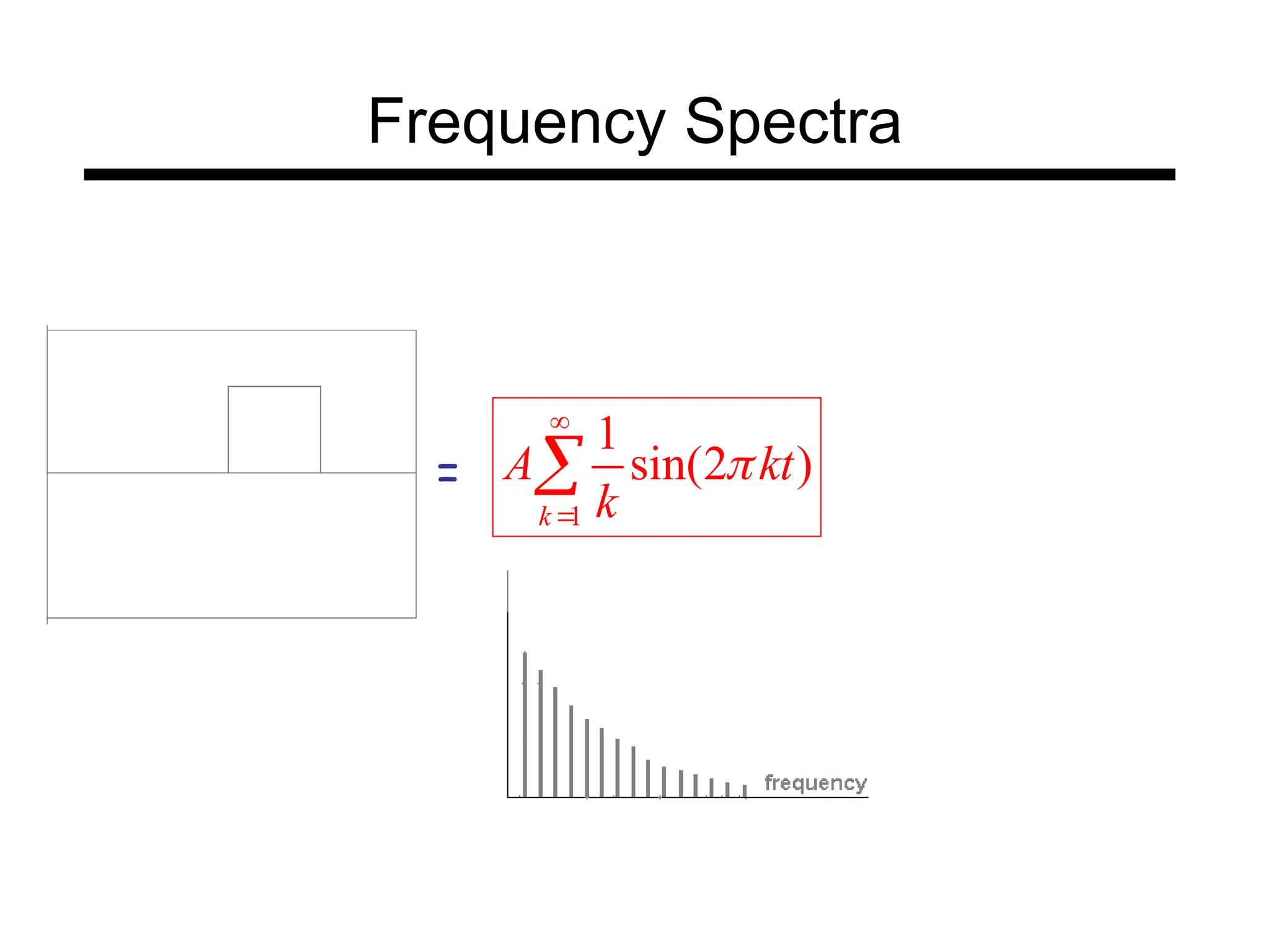
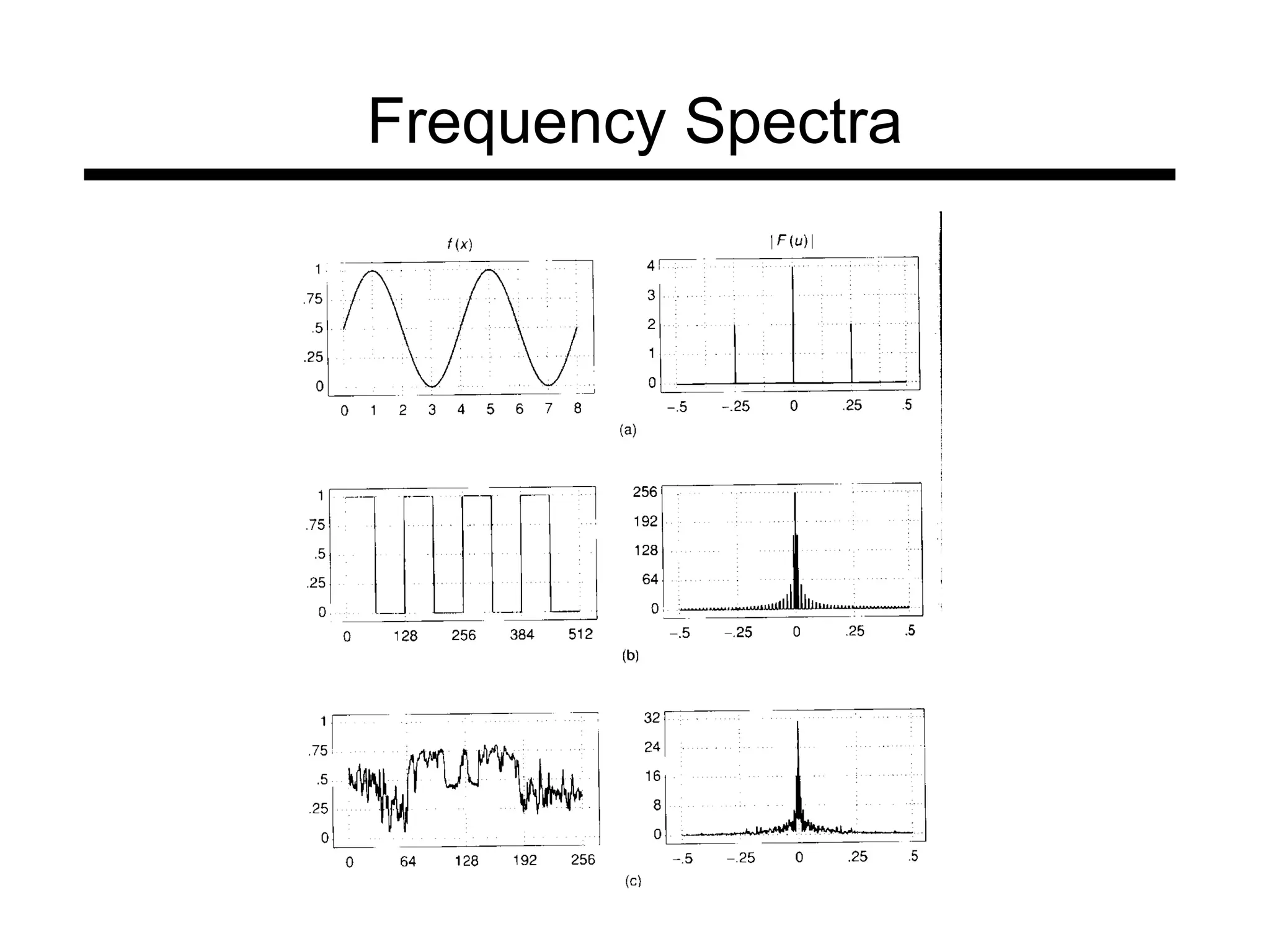
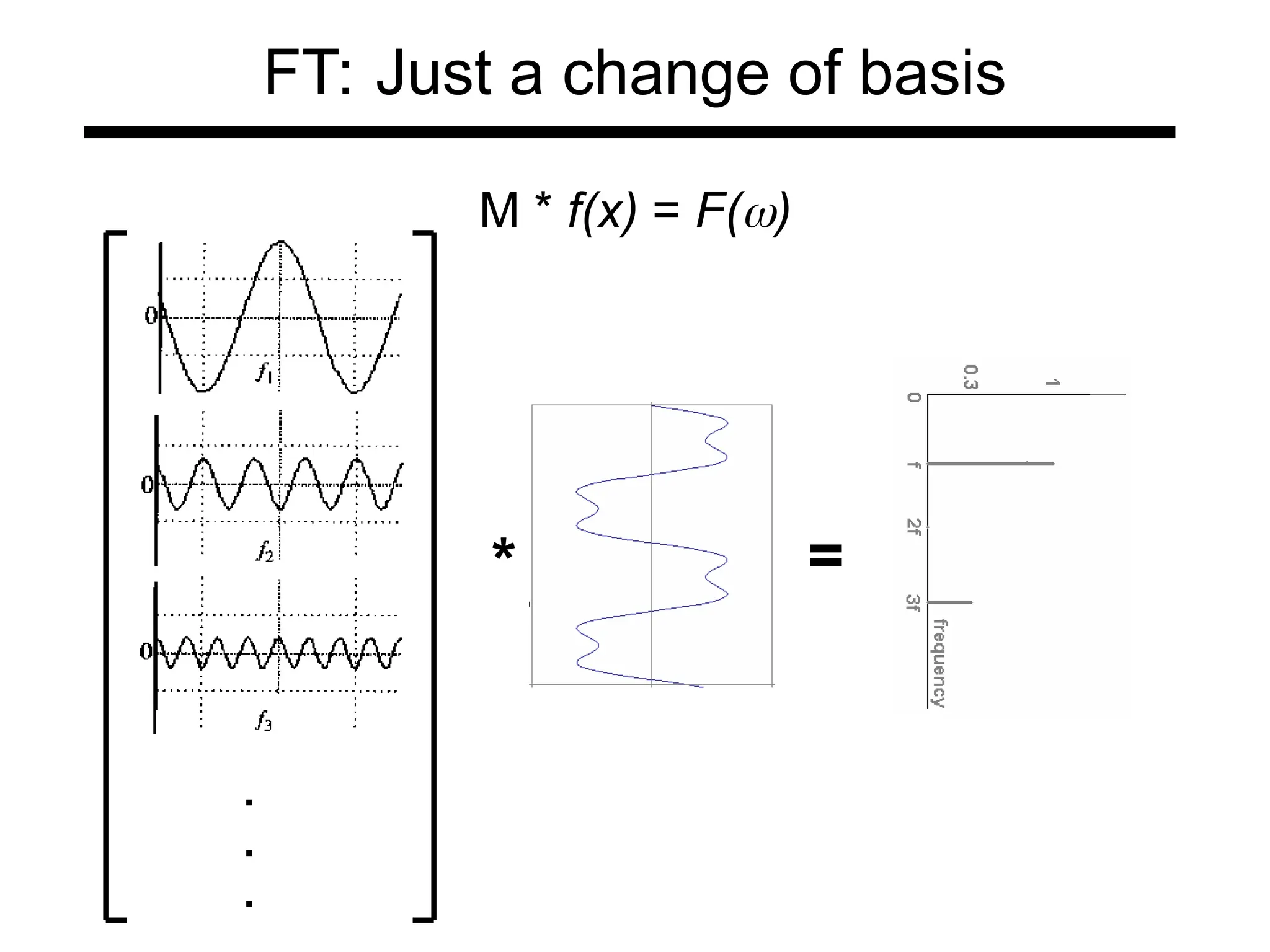
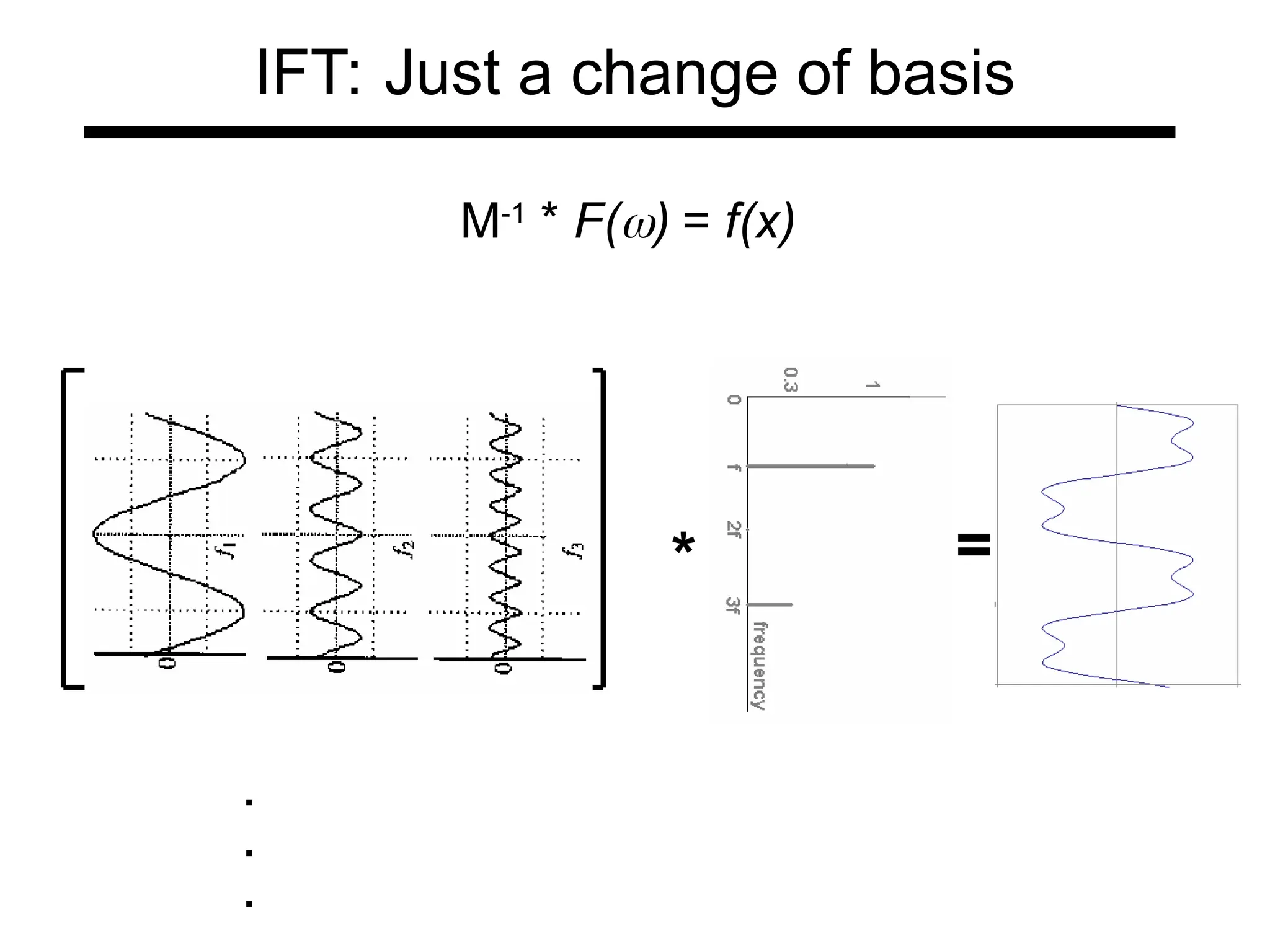
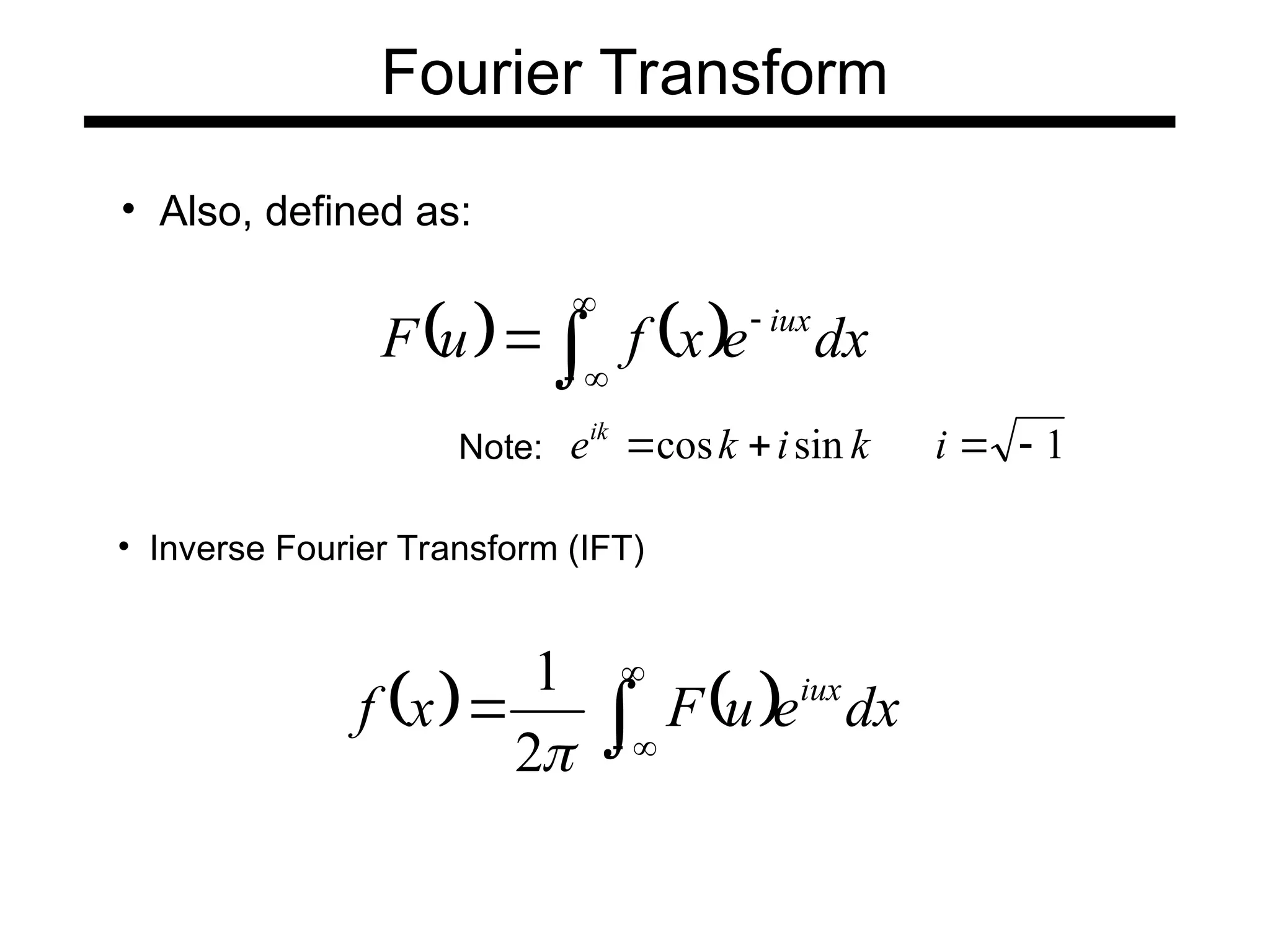
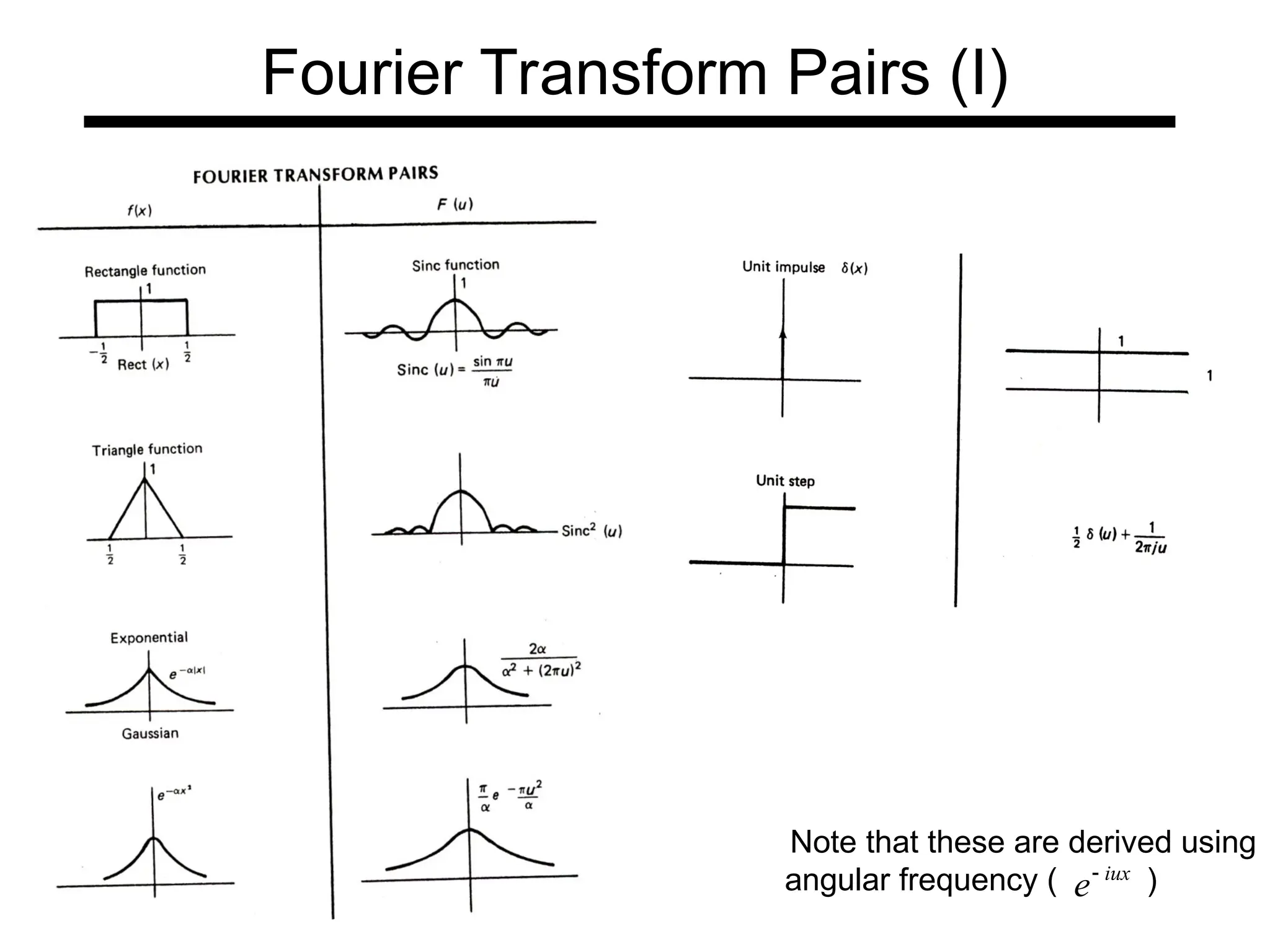
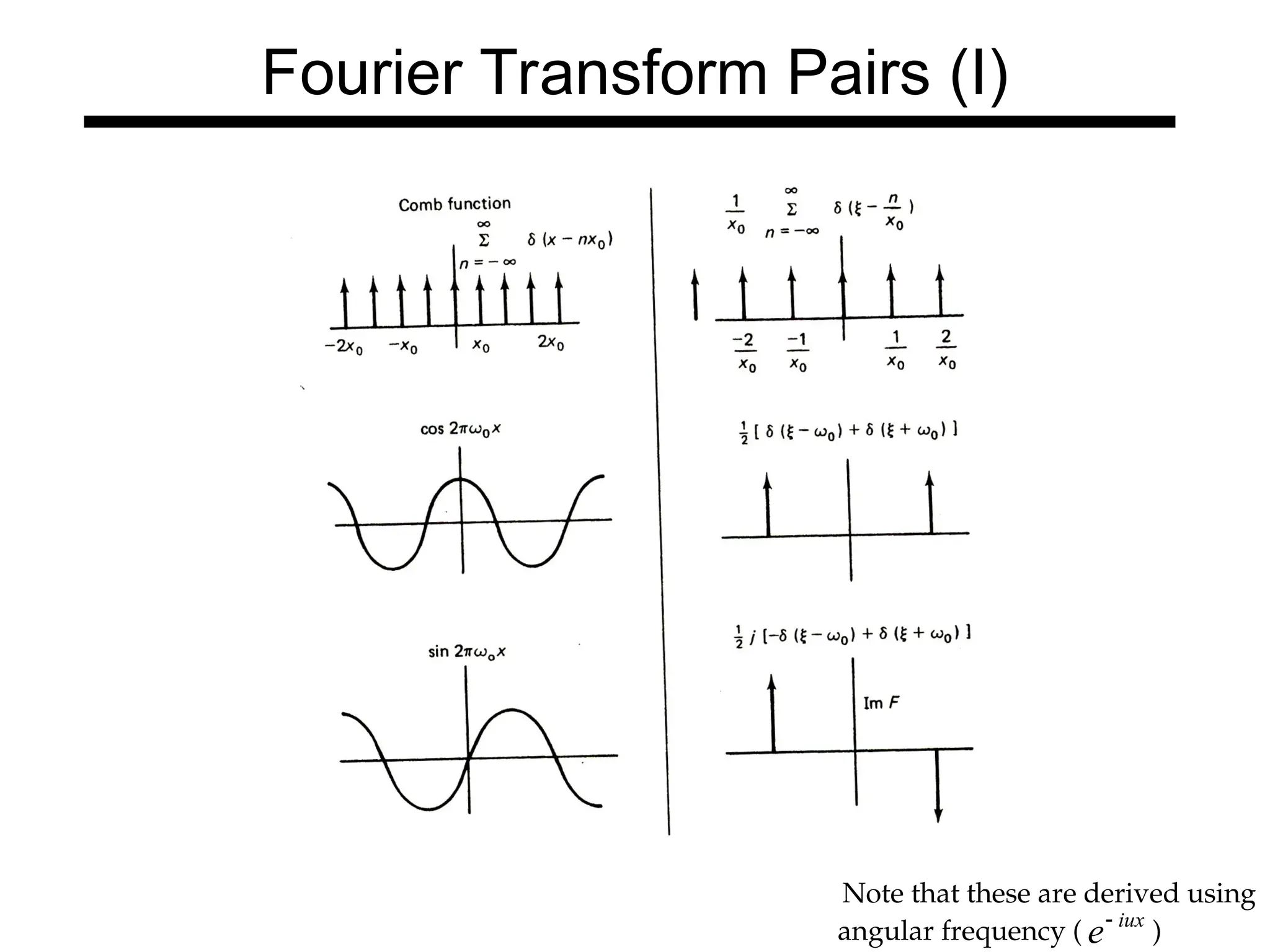
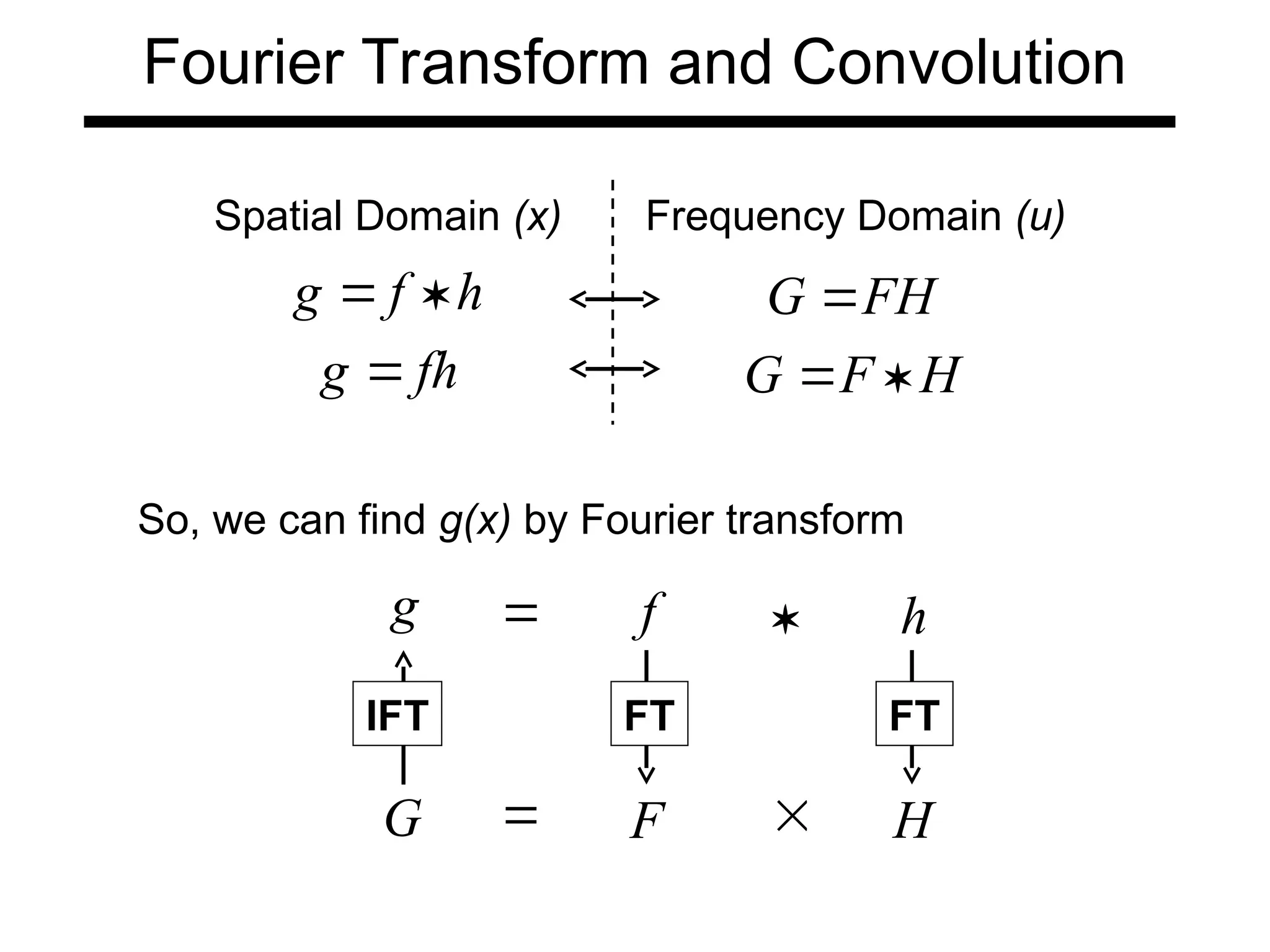
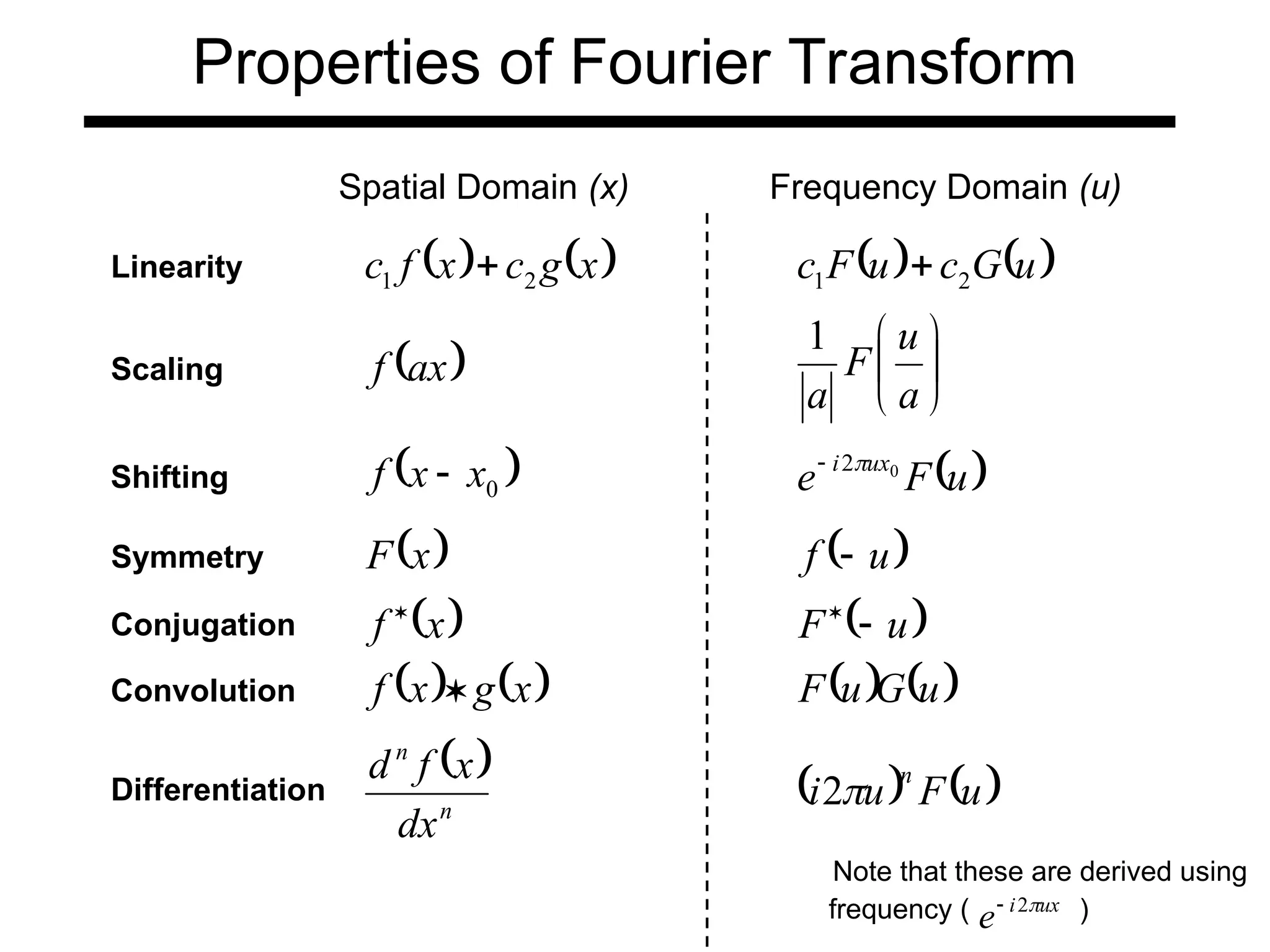
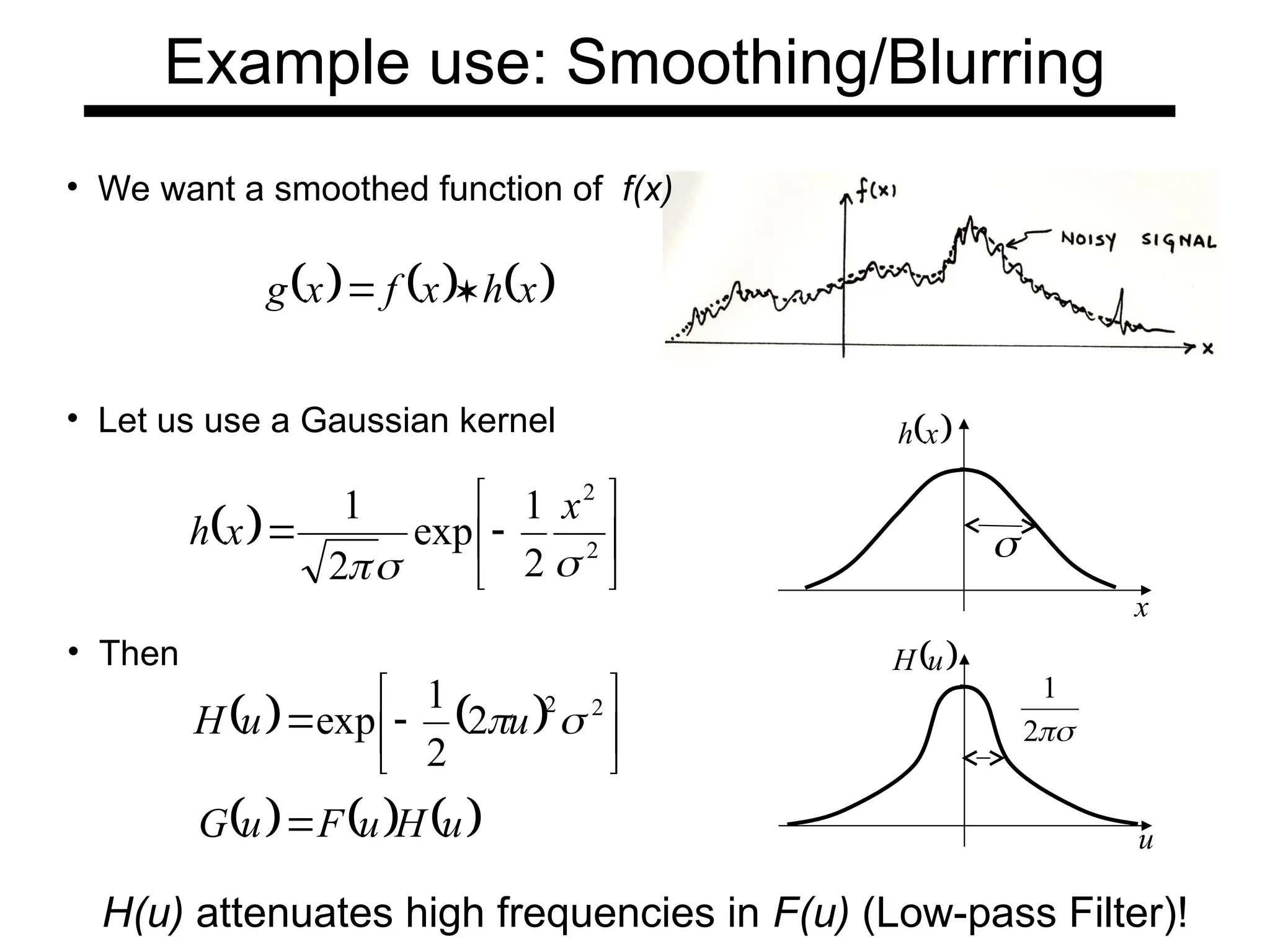
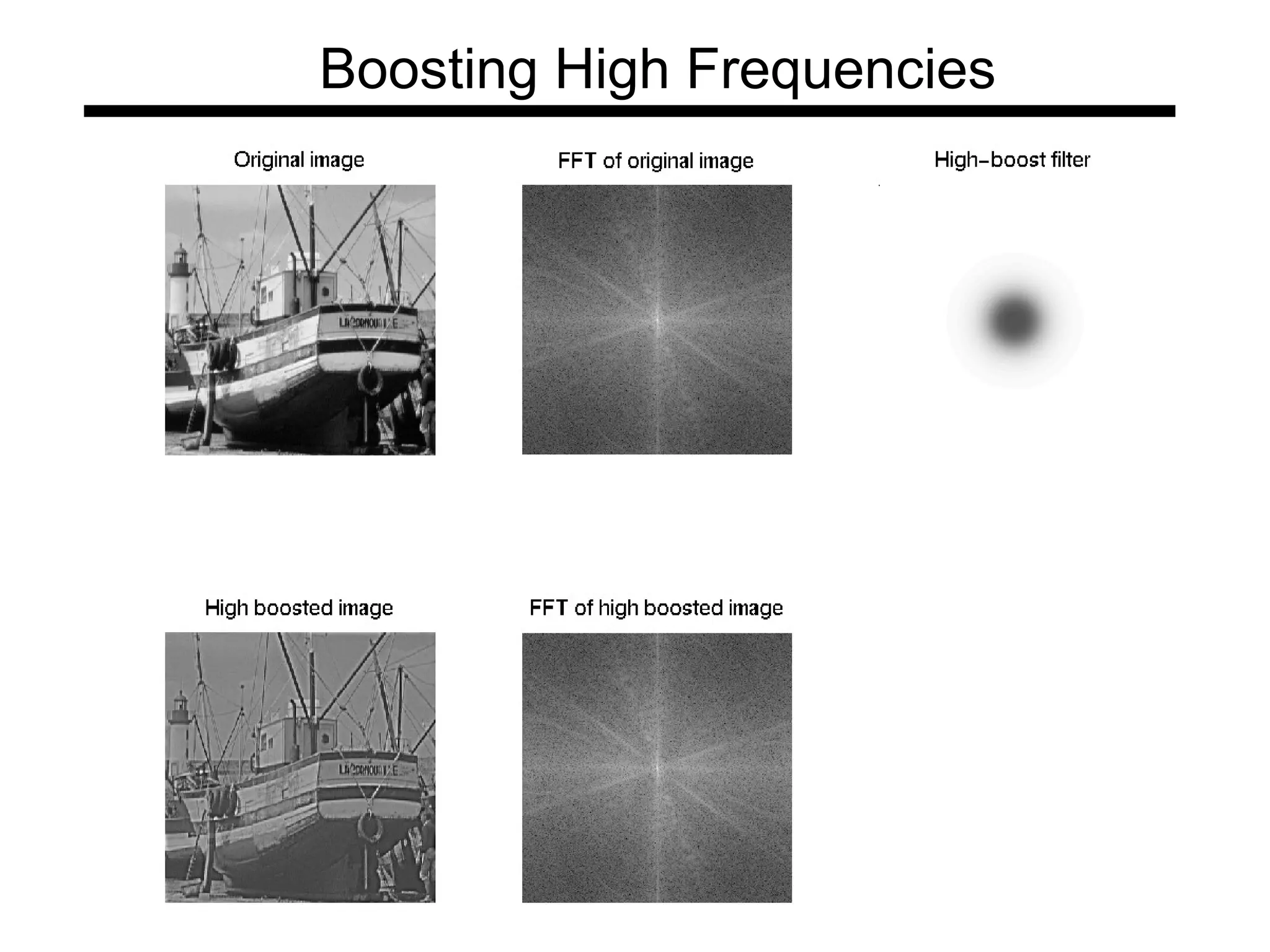
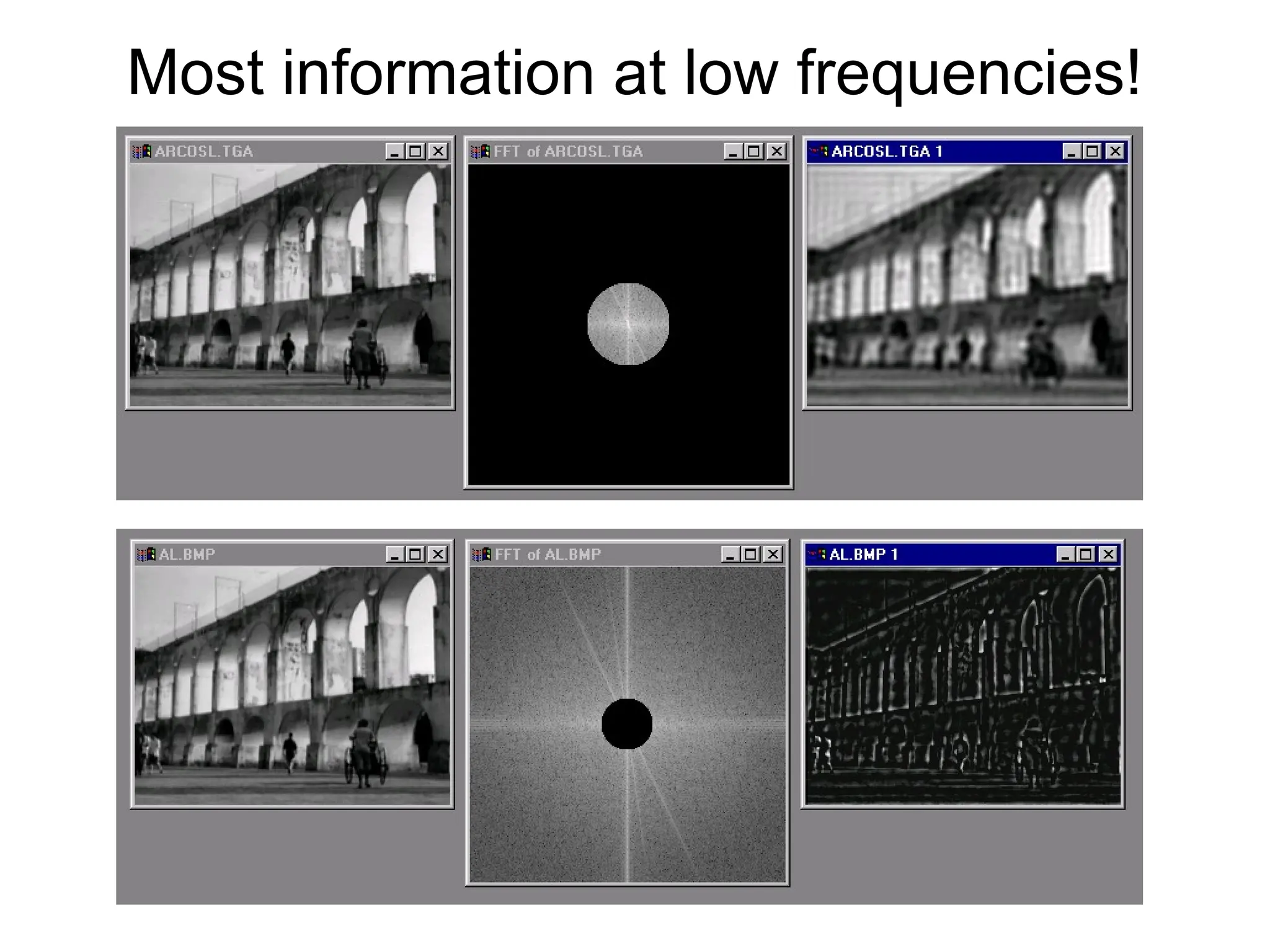
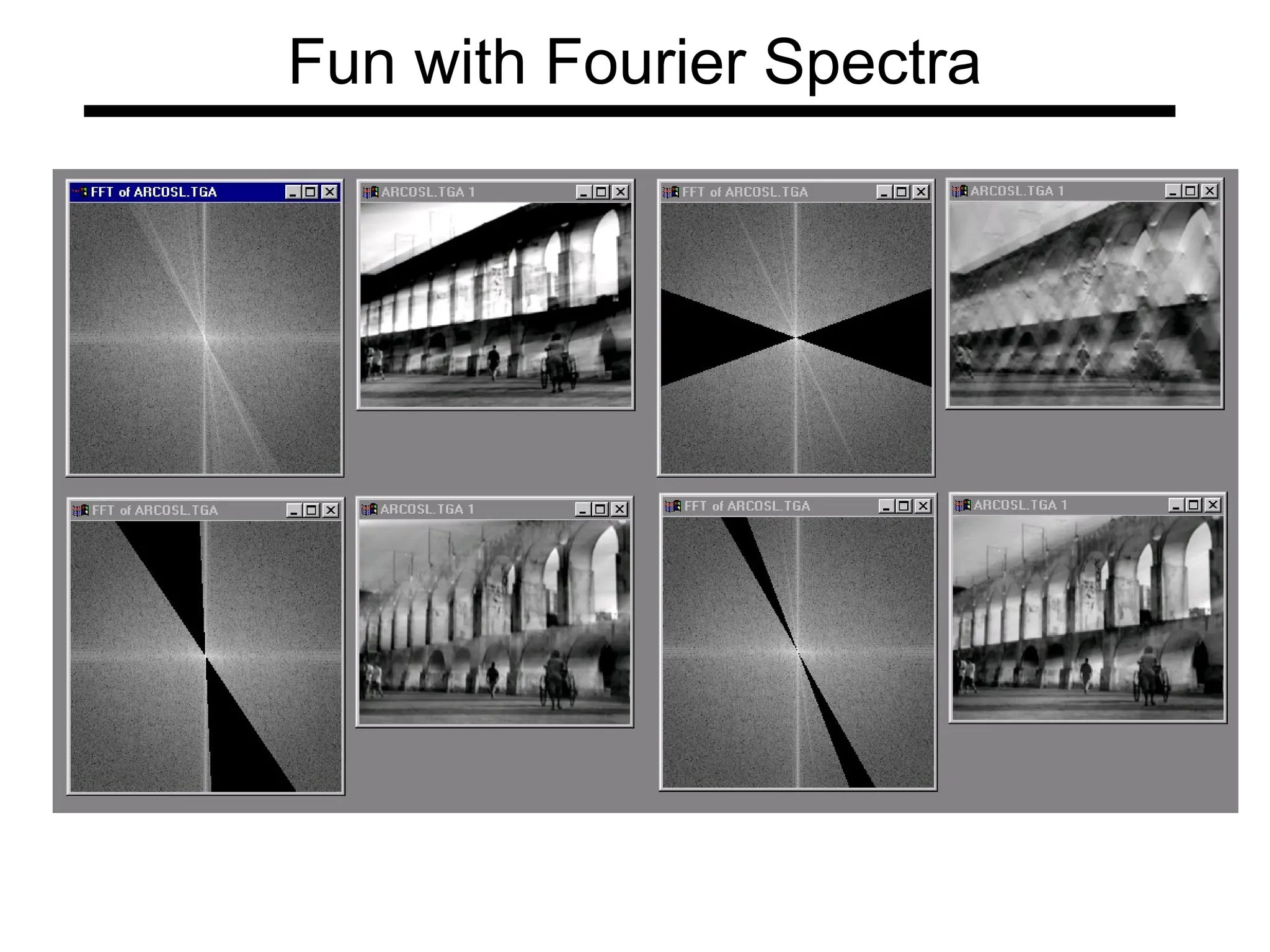
The document is a lecture on frequency domain analysis and Fourier transforms from a computer vision course. It discusses the representation of signals using Fourier series and transforms, emphasizing the significance of frequency over time in analyzing signals. It also covers properties and applications of Fourier transforms, such as convolution in spatial and frequency domains, and techniques like low-pass and high-pass filtering for image processing.

1. Computer Vision
Spring 2012 15-385,-685
Instructor: S. Narasimhan
Wean Hall 5409
T-R 10:30am – 11:50am

2. Frequency domain analysis and
Fourier Transform
Lecture #4

3. How to Represent Signals?
• Option 1: Taylor series represents any function using
polynomials.
• Polynomials are not the best - unstable and not very
physically meaningful.
• Easier to talk about “signals” in terms of its “frequencies”
(how fast/often signals change, etc).

4. Jean Baptiste Joseph Fourier (1768-1830)
• Had crazy idea (1807):
• Any periodic
function can be rewritten as
a weighted sum of Sines and
Cosines of different
frequencies.
• Don’t believe it?
– Neither did Lagrange,
Laplace, Poisson and
other big wigs
– Not translated into
English until 1878!
• But it’s true!
– called Fourier Series
– Possibly the greatest tool
used in Engineering

5. A Sum of Sinusoids
• Our building block:
• Add enough of them to
get any signal f(x) you
want!
• How many degrees of
freedom?
• What does each control?
• Which one encodes the
coarse vs. fine structure of
the signal?


x
Asin(

6. Fourier Transform
• We want to understand the frequency of our signal. So, let’s
reparametrize the signal by  instead of x:


x
Asin(
f(x) F()
Fourier
Transform
F() f(x)
Inverse Fourier
Transform
• For every  from 0 to inf, F() holds the amplitude A and phase
of the corresponding sine
– How can F hold both? Complex number trick!
)
(
)
(
)
( 

 iI
R
F 

2
2
)
(
)
( 
 I
R
A 


)
(
)
(
tan 1



R
I



7. Time and Frequency
• example : g(t) = sin(2pi f t) + (1/3)sin(2pi (3f) t)

8. Time and Frequency
= +
• example : g(t) = sin(2pi f t) + (1/3)sin(2pi (3f) t)

9. Frequency Spectra
• example : g(t) = sin(2pi f t) + (1/3)sin(2pi (3f) t)
= +

10. Frequency Spectra
• Usually, frequency is more interesting than the phase

11. = +
=
Frequency Spectra

12. = +
=
Frequency Spectra

13. = +
=
Frequency Spectra

14. = +
=
Frequency Spectra

15. = +
=
Frequency Spectra

16. =
1
1
sin(2 )
k
A kt
k




Frequency Spectra

17. Frequency Spectra

18. FT: Just a change of basis
.
.
.
* =
M * f(x) = F()

19. IFT: Just a change of basis
.
.
.
* =
M-1
* F() = f(x)

20. Fourier Transform – more formally
Arbitrary function Single Analytic Expression
Spatial Domain (x) Frequency Domain (u)
Represent the signal as an infinite weighted sum
of an infinite number of sinusoids
   





 dx
e
x
f
u
F ux
i 
2
(Frequency Spectrum F(u))
1
sin
cos 


 i
k
i
k
eik
Note:
Inverse Fourier Transform (IFT)
   




 dx
e
u
F
x
f ux
i 
2

21. • Also, defined as:
   





 dx
e
x
f
u
F iux
1
sin
cos 


 i
k
i
k
eik
Note:
• Inverse Fourier Transform (IFT)
   




 dx
e
u
F
x
f iux

2
1
Fourier Transform

22. Fourier Transform Pairs (I)
angular frequency ( )
iux
e
Note that these are derived using

23. angular frequency ( )
iux
e
Note that these are derived using
Fourier Transform Pairs (I)

24. Fourier Transform and Convolution
h
f
g 

   





 dx
e
x
g
u
G ux
i 
2
   
 








 dx
d
e
x
h
f ux
i


 
2
 
     
 
 










 dx
e
x
h
d
e
f x
u
i
u
i 





 2
2
 
   
 
 








 '
' '
2
2
dx
e
x
h
d
e
f ux
i
u
i 




Let
Then
   
u
H
u
F

Convolution in spatial domain
Multiplication in frequency domain


25. Fourier Transform and Convolution
h
f
g 
 FH
G 
fh
g  H
F
G 

Spatial Domain (x) Frequency Domain (u)
So, we can find g(x) by Fourier transform
g  f  h
G  F  H
FT FT
IFT

26. Properties of Fourier Transform
Spatial Domain (x) Frequency Domain (u)
Linearity    
x
g
c
x
f
c 2
1     
u
G
c
u
F
c 2
1 
Scaling  
ax
f 





a
u
F
a
1
Shifting  
0
x
x
f   
u
F
e ux
i 0
2

Symmetry  
x
F  
u
f 
Conjugation  
x
f 
 
u
F 

Convolution    
x
g
x
f     
u
G
u
F
Differentiation
 
n
n
dx
x
f
d
   
u
F
u
i
n

2
frequency ( )
ux
i
e 
2

Note that these are derived using

27. Properties of Fourier Transform

28. Example use: Smoothing/Blurring
• We want a smoothed function of f(x)
     
x
h
x
f
x
g 

H(u) attenuates high frequencies in F(u) (Low-pass Filter)!
• Then
    






 2
2
2
2
1
exp 
u
u
H
     
u
H
u
F
u
G 

2
1
u
 
u
H
  






 2
2
2
1
exp
2
1



x
x
h
• Let us use a Gaussian kernel

 
x
h
x

29. Does not look anything like what we have seen
Magnitude of the FT
Image Processing in the Fourier Domain

30. Image Processing in the Fourier Domain
Does not look anything like what we have seen
Magnitude of the FT

31. Convolution is Multiplication in Fourier Domain
*
f(x,y)
h(x,y)
g(x,y)
|F(sx,sy)|
|H(sx,sy)|
|G(sx,sy)|

32. Low-pass Filtering
Let the low frequencies pass and eliminating the high frequencies.
Generates image with overall
shading, but not much detail

33. High-pass Filtering
Lets through the high frequencies (the detail), but eliminates the low
frequencies (the overall shape). It acts like an edge enhancer.

34. Boosting High Frequencies

35. Most information at low frequencies!

36. Fun with Fourier Spectra

37. Next Class
• Image resampling and image pyramids
• Horn, Chapter 6