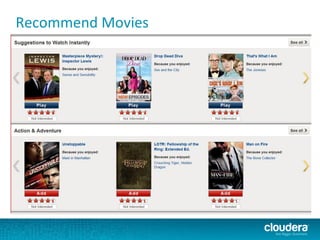
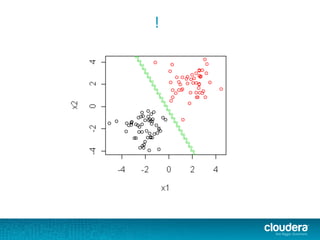
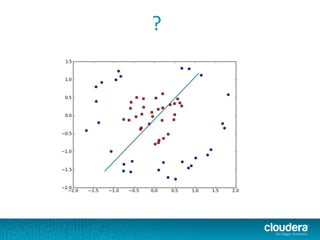
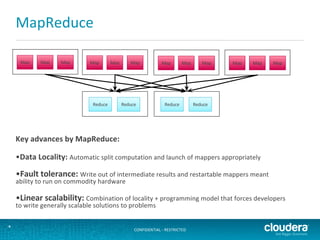
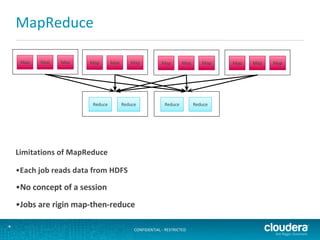
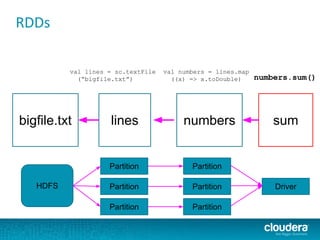
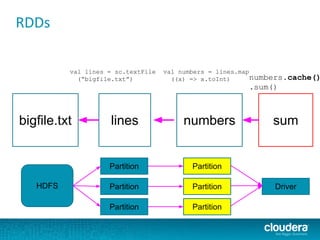
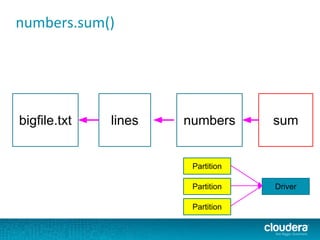
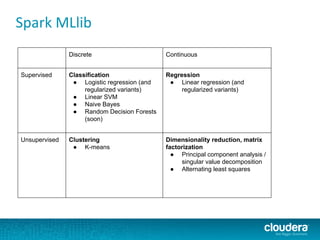
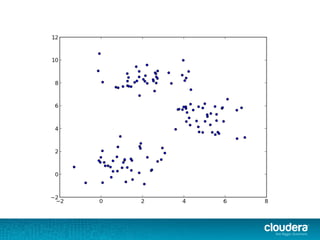
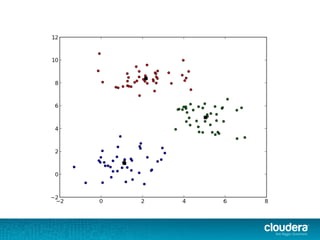
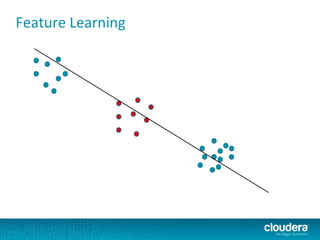
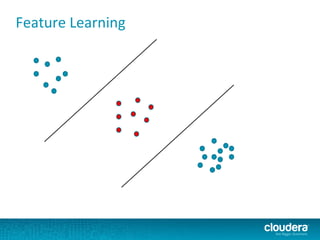
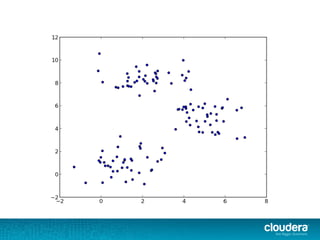
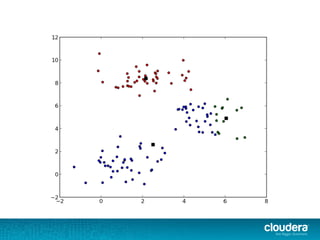
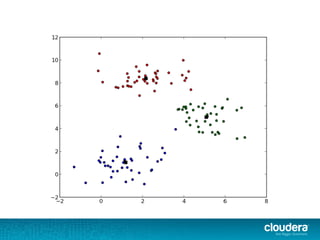
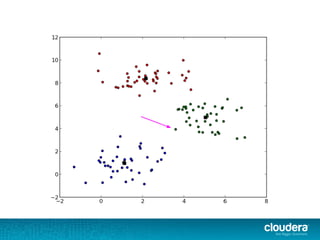
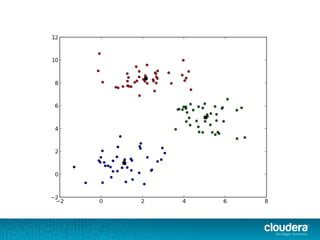
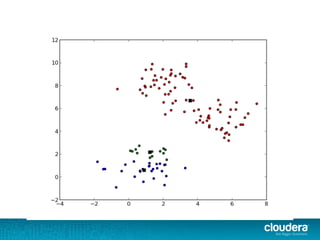
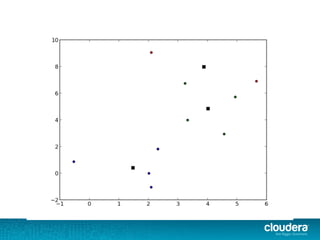
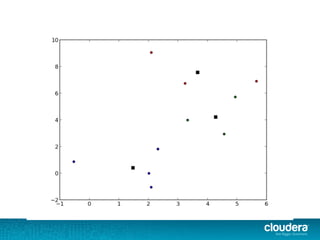
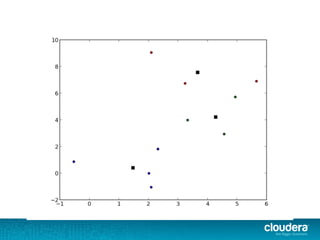
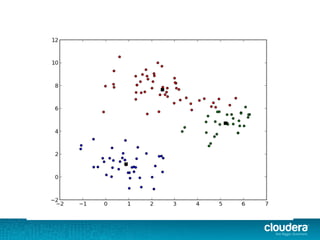
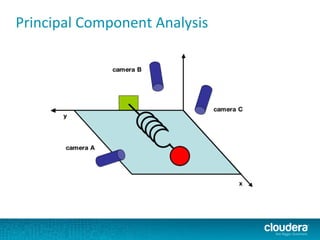
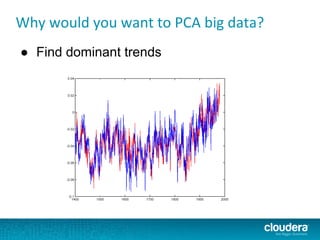
The document outlines the author's experience as a data scientist at Cloudera, focusing on developments in Apache Spark and Hadoop, as well as their academic background in combinatorial optimization and distributed systems. It discusses various data processing techniques, including clustering, dimensionality reduction, and algorithms for both supervised and unsupervised learning, notably k-means and principal component analysis. Additionally, it touches on challenges in choosing initial center points for k-means and introduces methods for feature learning and representation in high-dimensional data.

2. ● Data scientist at Cloudera
● Recently lead Apache Spark development at
Cloudera
● Before that, committing on Apache Hadoop
● Before that, studying combinatorial
optimization and distributed systems at
Brown

14. ● How many kinds of stuff are there?
● Why is some stuff not like the others?
● How do I contextualize new stuff?
● Is there a simpler way to represent this stuff?

15. ● Learn hidden structure of your data
● Interpret new data as it relates to this
structure

16. ● Clustering
○ Partition data into categories
● Dimensionality reduction
○ Find a condensed representation of your
data

17. ● Designing a system for processing huge
data in parallel
● Taking advantage of it with algorithms that
work well in parallel

21. bigfile.txt lines
val lines = sc.textFile
(“bigfile.txt”)
numbers
Partition
Partition
Partition
Partition
Partition
Partition
HDFS
sum
Driver
val numbers = lines.map
((x) => x.toDouble) numbers.sum()

23. bigfile.txt lines
val lines = sc.textFile
(“bigfile.txt”)
numbers
Partition
Partition
Partition
Partition
Partition
Partition
HDFS
sum
Driver
val numbers = lines.map
((x) => x.toInt) numbers.cache()
.sum()

24. bigfile.txt lines numbers
Partition
Partition
Partition
sum
Driver

27. Discrete Continuous
Supervised Classification
● Logistic regression (and
regularized variants)
● Linear SVM
● Naive Bayes
● Random Decision Forests
(soon)
Regression
● Linear regression (and
regularized variants)
Unsupervised Clustering
● K-means
Dimensionality reduction, matrix
factorization
● Principal component analysis /
singular value decomposition
● Alternating least squares

28. Discrete Continuous
Supervised Classification
● Logistic regression (and
regularized variants)
● Linear SVM
● Naive Bayes
● Random Decision Forests
(soon)
Regression
● Linear regression (and
regularized variants)
Unsupervised Clustering
● K-means
Dimensionality reduction, matrix
factorization
● Principal component analysis /
singular value decomposition
● Alternating least squares

31. ● Anomalies as data points far away from any
cluster

37. val data = sc.textFile("kmeans_data.txt")
val parsedData = data.map( _.split(' ').map(_.toDouble))
// Cluster the data into two classes using KMeans
val numIterations = 20
val numClusters = 2
val clusters = KMeans.train(parsedData, numClusters,
numIterations)

38. ● Alternate between two steps:
○ Assign each point to a cluster based on
existing centers
○ Recompute cluster centers from the
points in each cluster

44. ● Alternate between two steps:
○ Assign each point to a cluster based on
existing centers
■ Process each data point independently
○ Recompute cluster centers from the
points in each cluster
■ Average across partitions

45. // Find the sum and count of points mapping to each center
val totalContribs = data.mapPartitions { points =>
val k = centers.length
val dims = centers(0).vector.length
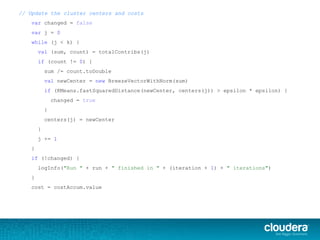
val sums = Array.fill(k)(BDV.zeros[Double](dims).asInstanceOf[BV[Double]])
val counts = Array.fill(k)(0L)
points.foreach { point =>
val (bestCenter, cost) = KMeans.findClosest(centers, point)
costAccum += cost
sums(bestCenter) += point.vector
counts(bestCenter) += 1
}
val contribs = for (j <- 0 until k) yield {
(j, (sums(j), counts(j)))
}
contribs.iterator
}.reduceByKey(mergeContribs).collectAsMap()

46. // Update the cluster centers and costs
var changed = false
var j = 0
while (j < k) {
val (sum, count) = totalContribs(j)
if (count != 0) {
sum /= count.toDouble
val newCenter = new BreezeVectorWithNorm(sum)
if (KMeans.fastSquaredDistance(newCenter, centers(j)) > epsilon * epsilon) {
changed = true
}
centers(j) = newCenter
}
j += 1
}
if (!changed) {
logInfo("Run " + run + " finished in " + (iteration + 1) + " iterations")
}
cost = costAccum.value

48. ● K-Means is very sensitive to initial set of
center points chosen.
● Best existing algorithm for choosing centers
is highly sequential.

50. ● Start with random point from dataset
● Pick another one randomly, with probability
proportional to distance from the closest
already chosen
● Repeat until initial centers chosen

51. ● Initial cluster has expected bound of O(log k)
of optimum cost

52. ● Requires k passes over the data

53. ● Do only a few (~5) passes
● Sample m points on each pass
● Oversample
● Run K-Means++ on sampled points to find
initial centers

63. Discrete Continuous
Supervised Classification
● Logistic regression (and
regularized variants)
● Linear SVM
● Naive Bayes
● Random Decision Forests
(soon)
Regression
● Linear regression (and
regularized variants)
Unsupervised Clustering
● K-means
Dimensionality reduction, matrix
factorization
● Principal
component
analysis / singular value
decomposition
● Alternating least squares

64. ● Select a basis for your data that
○ Is orthonormal
○ Maximizes variance along its axes

66. ● Find dominant trends

67. ● Find a lower-dimensional representation that
lets you visualize the data
● Feature learning - find a representation that’
s good for clustering or classification
● Latent Semantic Analysis

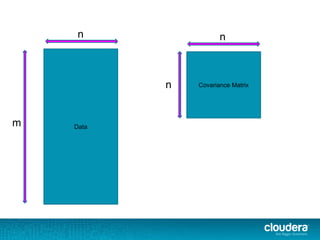
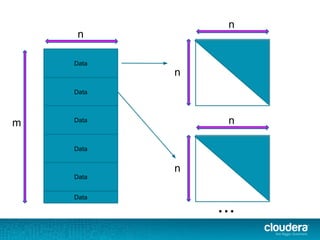
68. val data: RDD[Vector] = ...
val mat = new RowMatrix(data)
// compute the top 5 principal components
val principalComponents =
mat.computePrincipalComponents(5)
// project data into subspace
val transformed = data.map(_.toBreeze *
mat.toBreeze)

69. ● Center data
● Find covariance matrix
● Its eigenvectors are the principal
components

70. Datam
n
Covariance Matrix
n
n

71. Data
m
n
Data
Data
Data
Data
Data

72. Data
m
n
Data
Data
Data
Data
Data
n
n
n
n
...

73. Data
m
n
Data
Data
Data
Data
Data
n
n
n
n
... ...

74. n
n

75. n
n

76. n
n

77. def computeGramianMatrix (): Matrix = {
val n = numCols().toInt
val nt: Int = n * (n + 1) / 2
// Compute the upper triangular part of the gram matrix.
val GU = rows.aggregate( new BDV[Double](new Array[Double](nt)))(
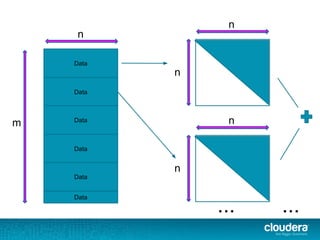
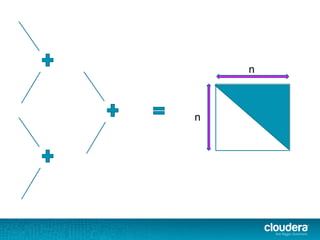
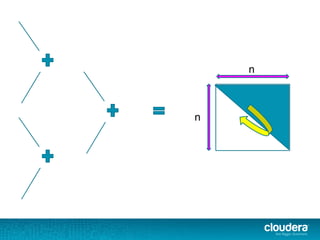
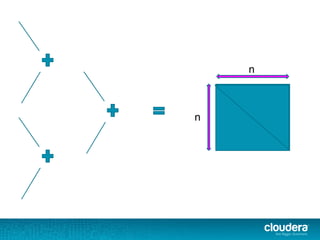
seqOp = (U, v) => {
RowMatrix.dspr( 1.0, v, U.data)
U
},
combOp = (U1, U2) => U1 += U2
)
RowMatrix.triuToFull(n, GU.data)
}

78. n
n

79. ● n^2 must fit in memory

80. ● n^2 must fit in memory
● Not yet implemented: EM algorithm can do it
with O(kn), where k is the number of
principal components