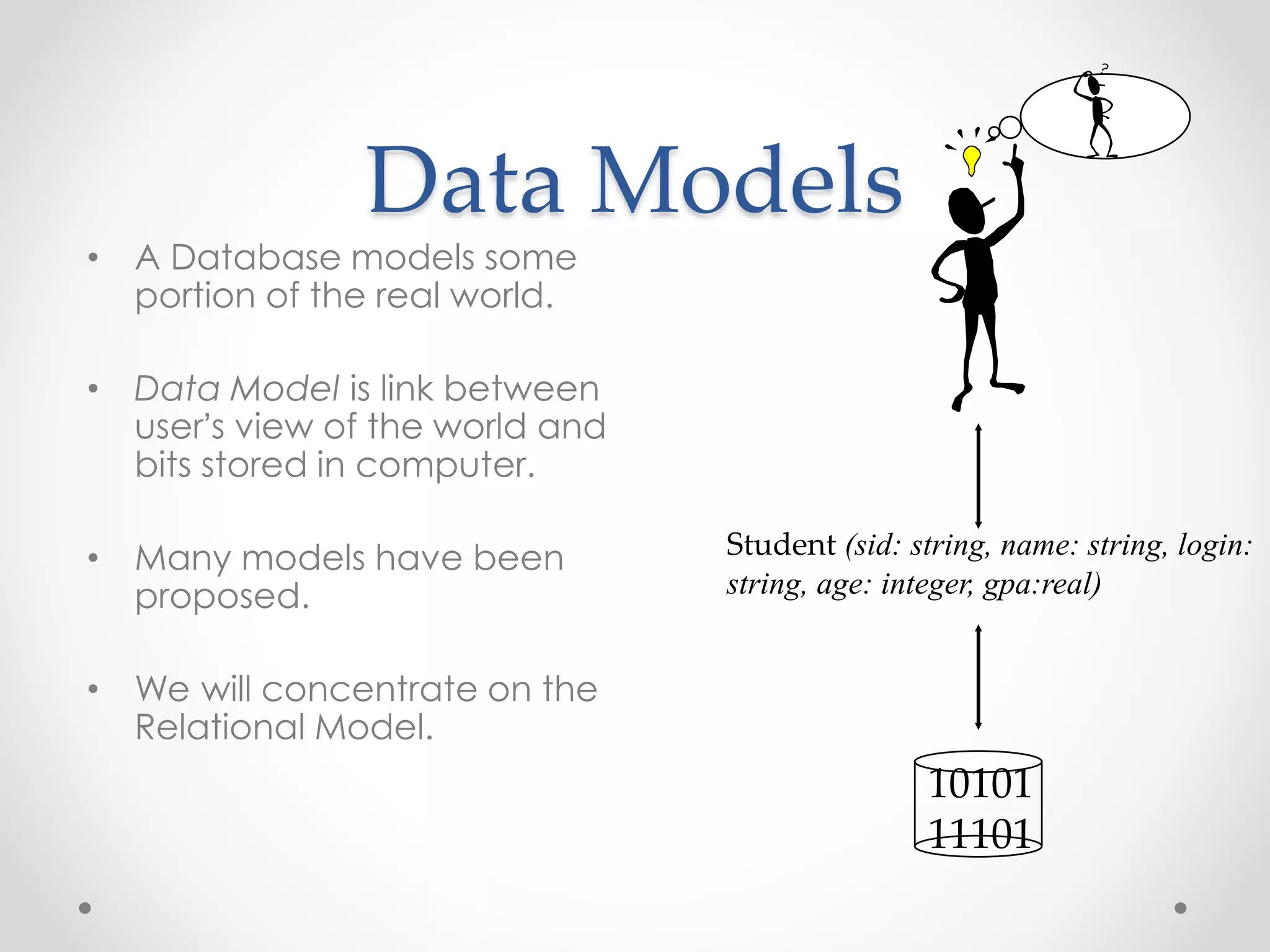
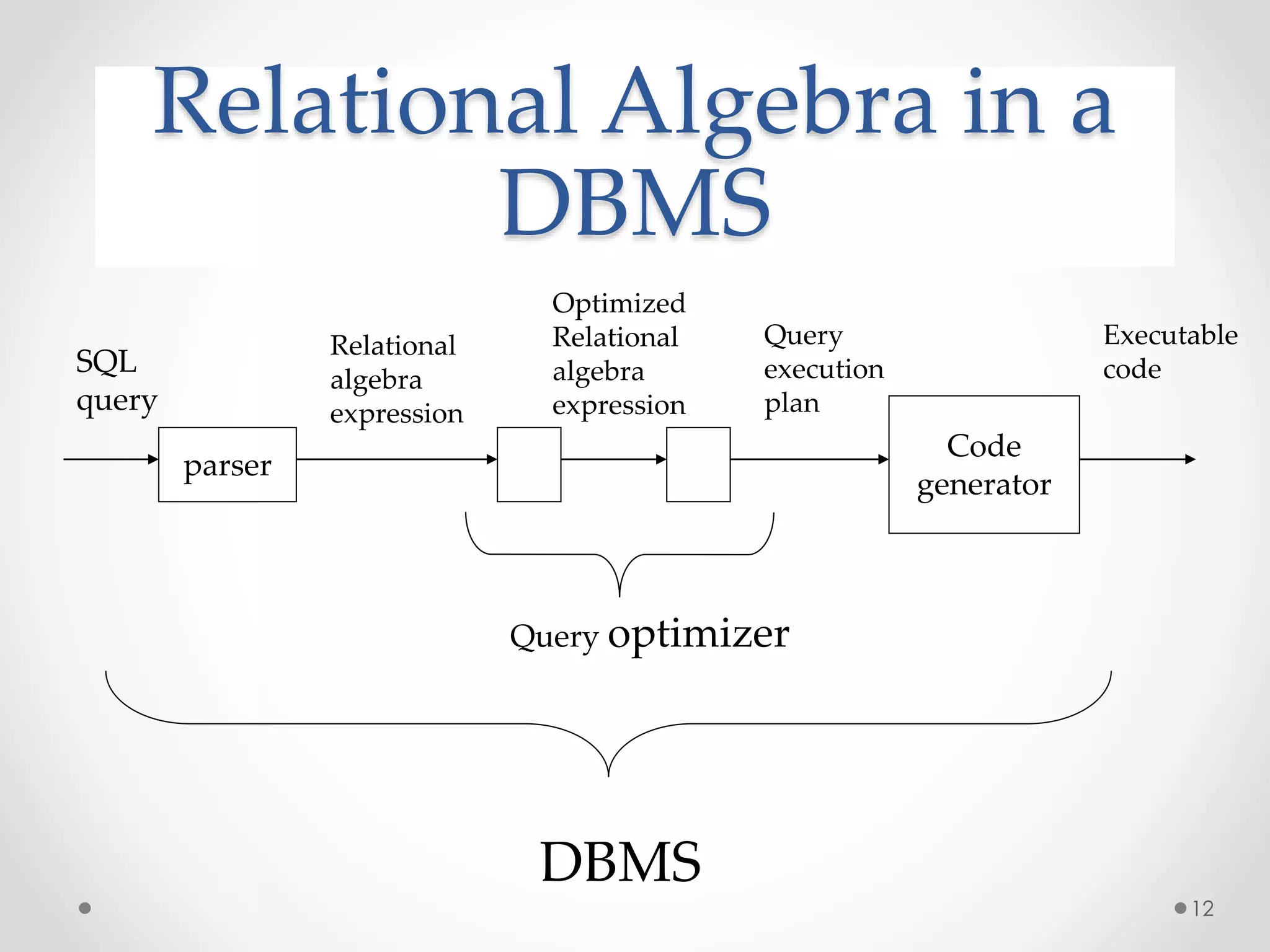
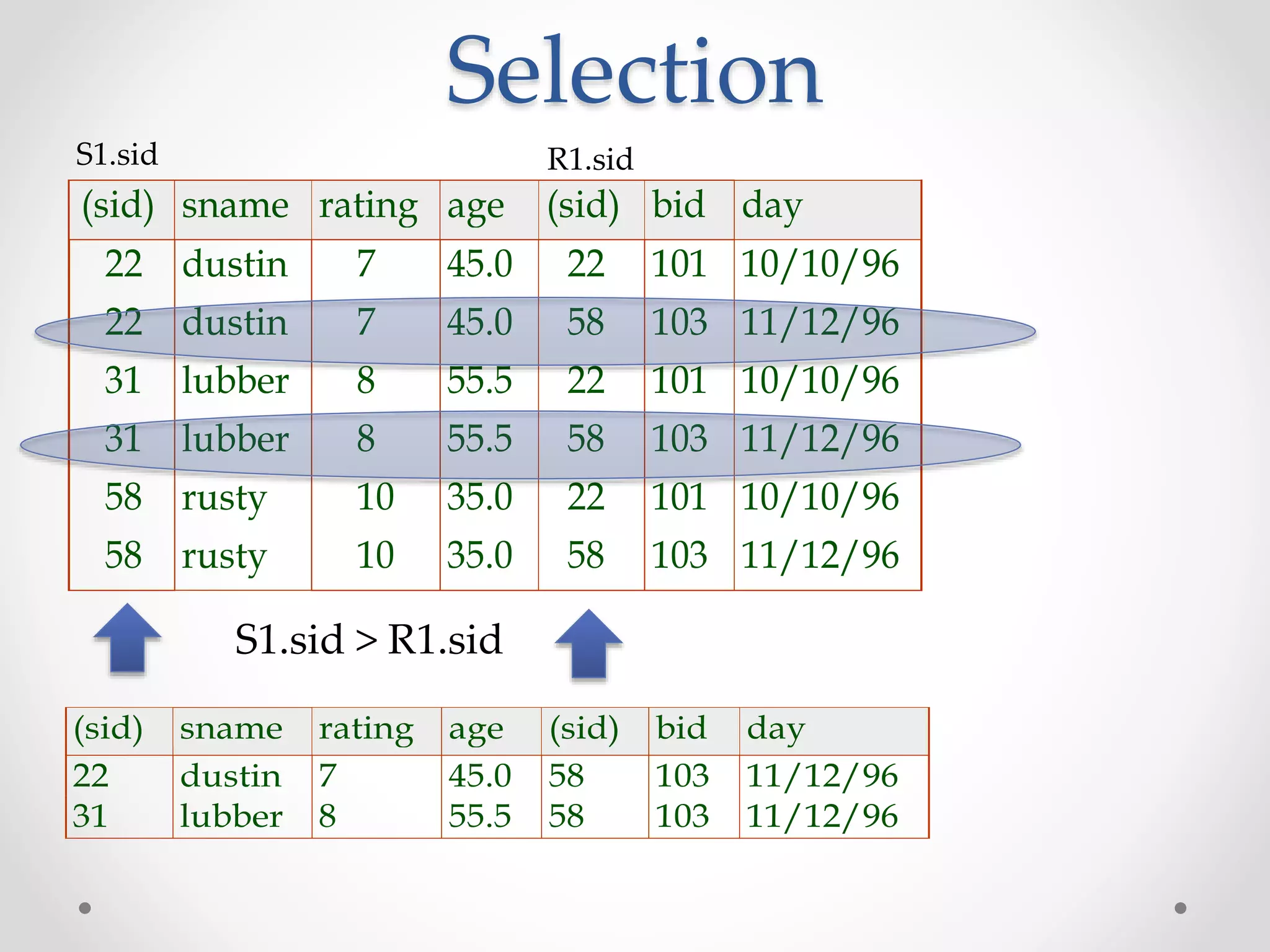
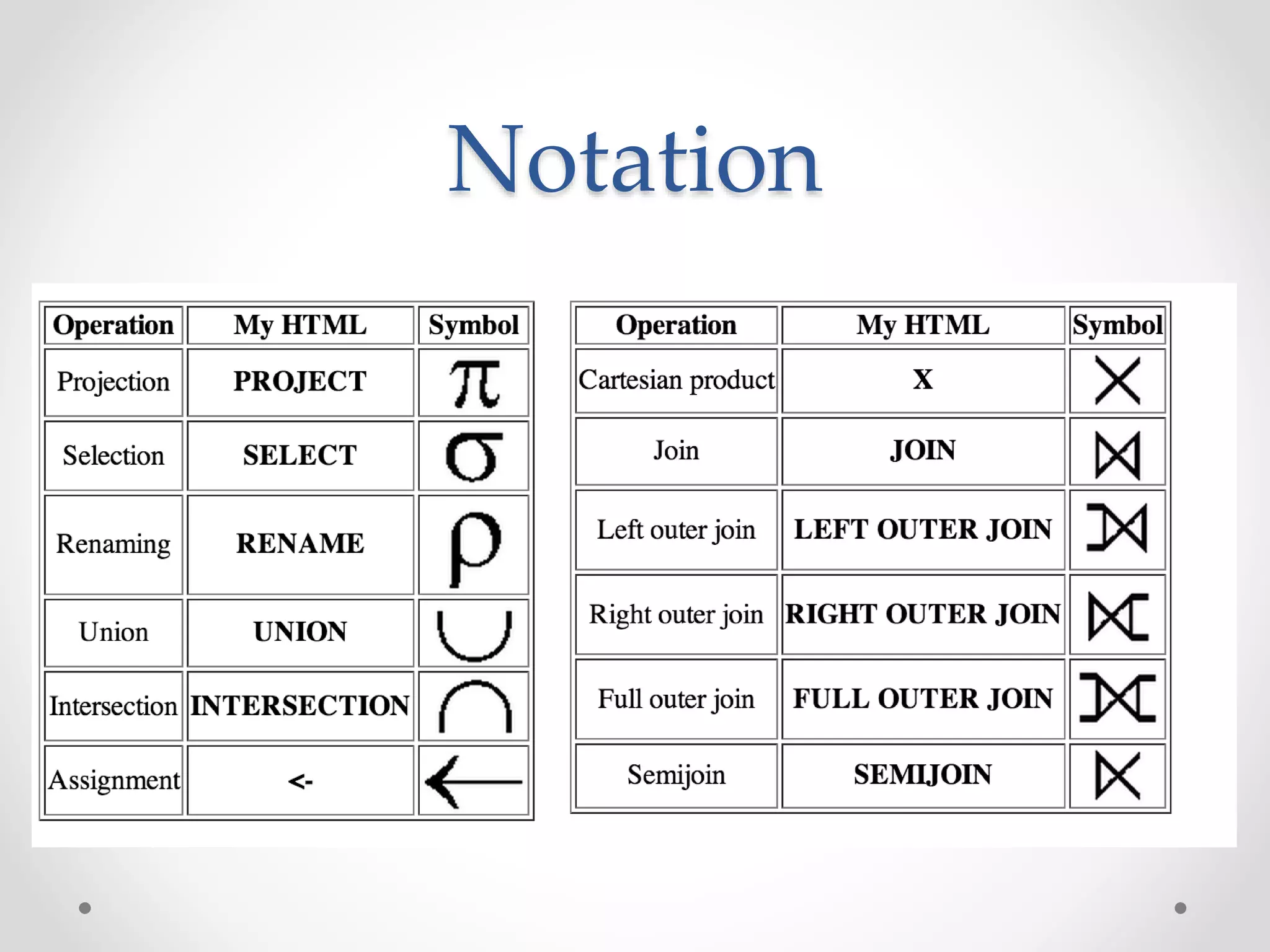
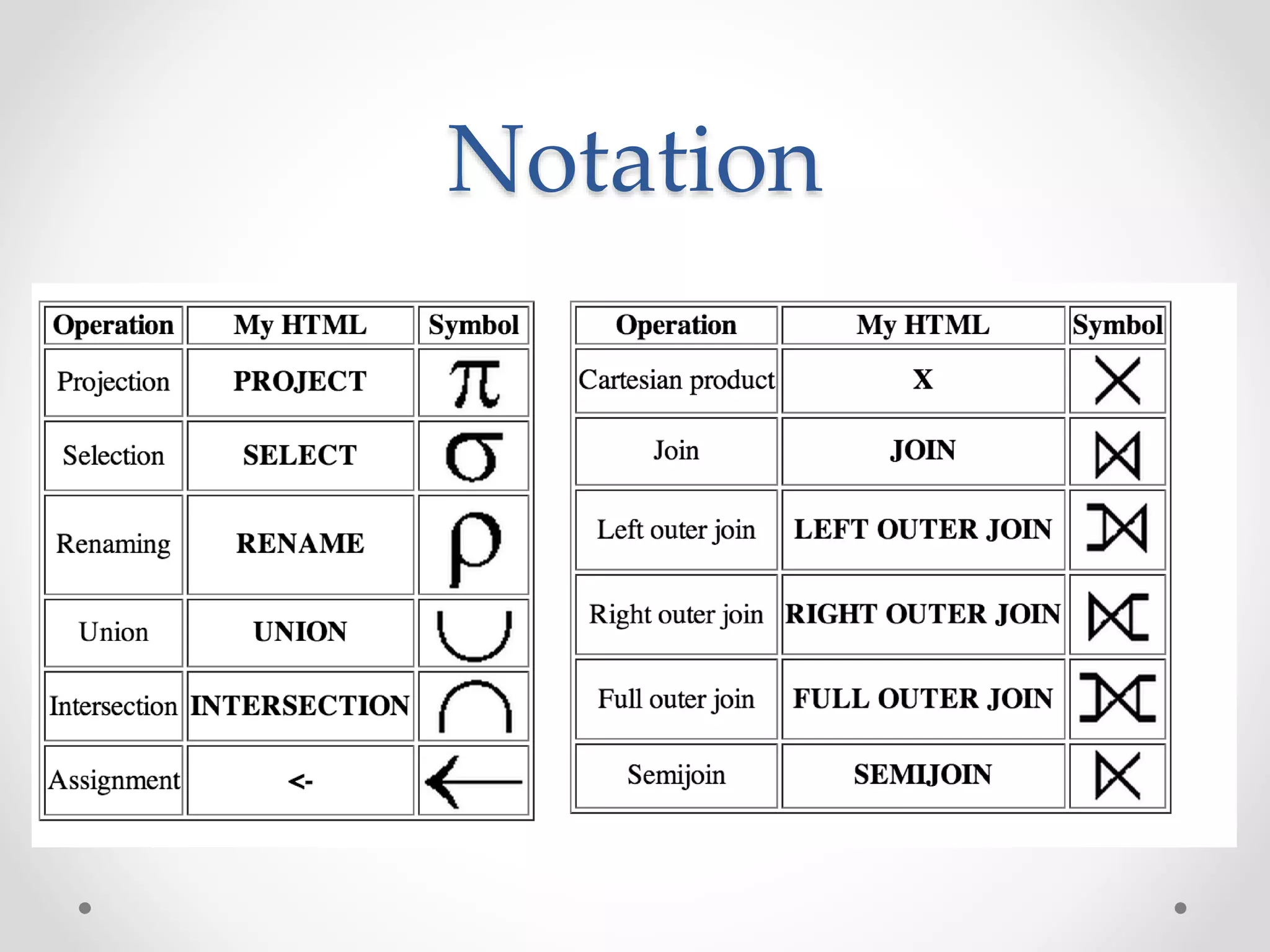
The document focuses on the relational model of data, which serves as a link between users' perceptions and stored data through tables known as relations, characterized by schemas and instances. It discusses the functionalities of relational query languages, primarily relational algebra and calculus, which provide methods for data manipulation and retrieval in a formal manner. Key operations in relational algebra include selection, projection, union, intersection, difference, and cross-product, which are closed operations, allowing for the creation of composite functions essential for effective database querying.