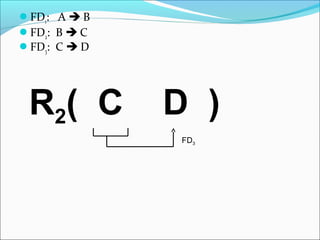
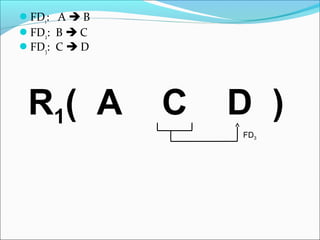
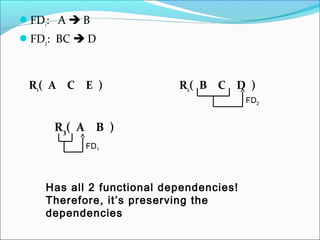
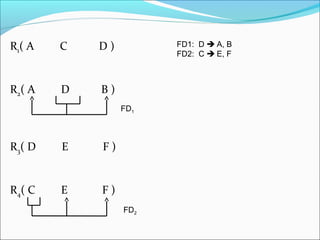
The document discusses dependency preservation in database decomposition. It defines dependency preservation as a decomposition where the union of functional dependencies (FDs) projected onto each individual relation is equivalent to the FDs of the original relation. This allows FDs to be checked locally without joins. An example shows a decomposition that preserves three FDs, while another loses an FD and is thus not dependency preserving. The document provides guidance on how to determine if a given decomposition preserves the dependencies of the original relation.

1. MANASY JAYASURYA
Dept. of Computer Science & Applications
St.Mary’s College,Thrissur

2. Why Do We Preserve The Dependency?
We would like to check easily that updates to the database
do not result in illegal relations being created.
It would be nice if our design allowed us to check updates
without having to compute natural joins.

3. Definition
A decomposition D = {R1, R2, ..., Rn} of R is
dependency-preserving with respect to F if the union
of the projections of F on each Ri in D is equivalent to
F; that is
if (F1 ∪ F2∪ … ∪ Fn)+
= F +

4. In Layman’s Term
Each Functional Dependency specified in F
either appears directly in one of the
relations in the decomposition.

5. Continue…
It is not necessary that all dependencies from the
relation R appear in some relation Ri. It is sufficient
that the union of the dependencies on all the
relations Ri be equivalent to the dependencies on R.

6. Property of Dependency-Preservation
If a decomposition is not dependency-preserving,
therefore, that dependency is lost in the
decomposition.
FD1
FD2
FD3
FD4

7. Example of Dependency Preservation
R(A B C D)
FD1: A  B
FD2: B  C
FD3: C  D
Decomposition:
R1(A B C) R2(C D)

8. FD1: A  B
FD2: B  C
FD3: C  D
FD1
FD2
R1( A B C )

9. FD1: A  B
FD2: B  C
FD3: C  D
FD3
R2( C D )

10. FD1: A  B
FD2: B  C
FD3: C  D
R1( A B C ) R2( C D )
Has all 3 functional dependencies!
Therefore, it’s preserving the
dependencies
FD1
FD2
FD3

11. Example of Non-Dependency Preservation
R(A B C D)
FD1: A  B
FD2: B  C
FD3: C  D
Decomposition:
R1(A C D) R2(B C)

12. FD1: A  B
FD2: B  C
FD3: C  D
FD3
R1( A C D )

13. FD1: A  B
FD2: B  C
FD3: C  D
FD2
R2( B C )

14. FD1: A  B
FD2: B  C
FD3: C  D
R1( A C D ) R2( B C )
Does not support FD1: A => B
Therefore, it does not preserve the
dependencies
FD3
FD2

15. More Example
R(A B C D E)
FD1: A  B
FD2: BC  D
Decomposition:
R1(A C E) R2(B C D) R3(A B)

16. FD1: A  B
FD2: BC  D
R1( A C E )
No Dependencies

17. FD1: A  B
FD2: BC  D
FD2
R2( B C D )

18. FD1: A  B
FD2: BC  D
FD1
R3( A B )

19. FD1: A  B
FD2: BC  D
R1( A C E ) R2( B C D )
Has all 2 functional dependencies!
Therefore, it’s preserving the
dependencies
FD1
FD2
R3( A B )

20. Exercise Problem

21. R(A, B, C, D, E, F )
FD1: D  A, B
FD2: C  E, F
Decomposition:
R1( A, C, D )
R2( A, D, B )
R3( D, E, F )
R4( C, E, F )

22. R1( A C D )
R2( A D B )
R3( D E F )
R4( C E F )
FD1
FD2
FD1: D  A, B
FD2: C  E, F

23. Answer
Yes!
This is a dependency-preservation