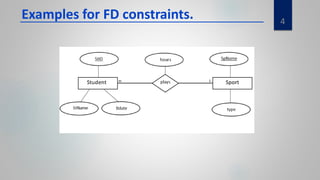
Functional dependencies (FDs) describe relationships between attributes in a database relation. FDs constrain the values that can appear across attributes for each tuple. They are used to define database normalization forms. Some examples of FDs are: student ID determines student name and birthdate; sport name determines sport type; student ID and sport name determine hours practiced per week. FDs can be trivial, non-trivial, multi-valued, or transitive. Armstrong's axioms provide rules for inferring new FDs. The closure of a set of attributes includes all attributes functionally determined by that set according to the FDs. Closures are used to identify keys, prime attributes, and equivalence of FDs.

1. Functional
Dependencies
R L D D Rajapaksha
Diploma in Software Application Development
Wayamba University of Sri Lanka, Kuliyapitiya
13 May 2018

2. 2
Functional Dependencies…?
• Functional Dependency (FD) is a constraint that describes
the relationship between attributes in the relation (table).
• FDs and Keys are used to define the normal forms for
relations.

3. 3
Functional Dependencies…? (cont…)
Definition :
Relation schema: R {A1,A2,...,An}
X , Y are subsets of R
If R: X Y then,
If t1[X]=t2[X] then,
t1[Y]=t2[Y] in any relation instance r(R)
R
t2
t1
YX

4. 4
Examples for FD constraints.

5. 5
Examples for FD constraints.
• Student ID determines Student name and Birth date.
StID  {StName, Bdate}
• Sport Name determines type of sport.
SpName  type
• Student ID and Sport Name determine the hours per week that
the student practices his sport.
{StID, SpName}  hours

6. 6
Functional Dependencies…? (cont…)
• A FD is a property of attributes in the relational schema R
(intension).
• If L is a key of the relation R, it determines all the attributes of
R.

7. 7
Inference Rules for FDs.
• Armstrong's inference rules
A1. (Reflexive) If Y subset-of X, then X  Y
A2. (Augmentation) If X  Y, then XZ  YZ
(Notation: XZ stands for X U Z)
A3. (Transitive) If X  Y and Y  Z, then X  Z
Go back Slide 14

8. 8
Additional Useful Inference Rules.
• Decomposition
If X  YZ, then X  Y and X  Z
• Union
If X  Y and X  Z, then X  YZ
• Psuedotransitivity
If X  Y and WY  Z, then WX  Z

9. 9
Types of Functional Dependencies.
1. Trivial Functional Dependency.
2. Non-Trivial Functional Dependency.
3. Multi-valued Dependency.
4. Transitivity Dependency.

10. 10
1. Trivial Functional Dependency.
• The dependency of an attribute on a set of attributes is known
as trivial functional dependency if the set of attributes includes
that attribute.
If B is a subset of A then,
ABB
AA
BB
A B

11. 11
2. Non-Trivial Functional Dependency.
• If a functional dependency X->Y holds true where Y is not a
subset of X
If B is not a subset of A then,
AB
A B

12. 12
3. Multi-valued Dependency.
• If there are more than one independent multi-valued attributes
in a relation, that is called “multi-valued dependency”.
bike_model manf_year colour
V001 2011 Black
V001 2011 Blue
V002 2012 Black
V002 2012 Blue
V003 2013 Black
V003 2013 Blue
bike_model ->> manf_year
bike_model ->> colour

13. 13
4. Transitivity Dependency.
• A functional dependency is said to be transitive if it is indirectly
formed by two functional dependencies.
Transitive dependency: XZ;
if the following three functional dependencies hold TRUE,
XY
Y does not X
YZ
• Can only occur in a relation of three or more attributes.
• Helps to normalizing the DB in 3NF.

14. 14
Example_Transitivity Dependency.
Book Author Author_Age
ABC Nimal Bandara 48
XY Sakunthala Weerasinghe 36
MNO Nimal Bandara 48
{Book}  {Author}
{Author} does not  {Book}
{Book} { Author_Age}
Therefore Transitive Dependency is;
{Book}  {Author_Age} ; inference rules

15. 15
Closure of Functional Dependency.
Closure of a set (X+) is the set of attributes functionally determined by
X.
Let S be the set of functional dependencies on relation R. Let X is set
of attributes that appear on left hand side of some FD in S and we
want to determine the set of all attributes that are dependent on X.
Thus for each such set of attribute X, we determine the set X+ of
attributes that are functionally determined by X based on S, X+ is
called closure of X under S
-www.edugrabs.com-

16. 16
Example_Closure of Functional Dependency.
Closure of A (A+)
A+ = A
A(BC) ; from (1)
AB(CD)C ; from (2)
ABCDC = ABCD
So, A+ = ABCD
A B C D
Functional Dependencies:
(1); A  BC
(2); B  CD

17. 17
Applications_Closure of Functional Dependency.
• It is used to identify the additional FDs.
• It is used to identify keys(CKs and SKs).
• It is used to identify the Prime and Non-Prime Attributes.
• It is used to identify equivalence of FD.

18. THANK YOU
18