Computability, turing machines and lambda calculus

Programming Languages and
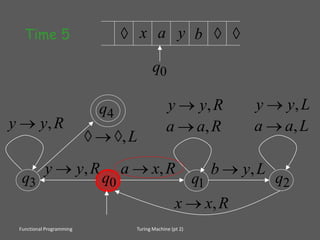
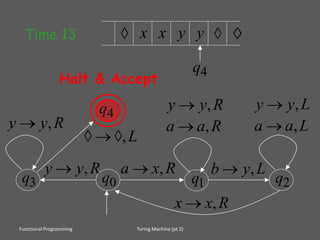
Paradigms
Functional Programming Background
(computability, turing machines, lambda calculus)
Edward (Ned) Blurock
Functional Programming Functional Programming

COMPUTABILITY
Will an algorithm be able to compute the task?
Is the task I want impossible?
Is it possible to formulate an impossible task?
What is the consequences for other algorithms
Functional Programming Computability

Computability vs Complexity
• Computability refers to whether of not in
principle it is possible to evaluate f(n) by
following a set of instructions.
• We are not for the moment worried if this
computation requires 1,000,000 or more
consecutive steps.
• The latter refers to complexity which we will
return to later.

Ensheidungsproblem
Decision problem
Hilbert 1928
The Entscheidungsproblem asks for
an algorithm
that takes as input a statement of a first-order logic
and
answers "Yes" or "No"
according to whether the statement is universally valid
(valid in every structure satisfying the axioms).
An algorithm to ask whether something is true
Is it computableFunctional Programming Computability

Ensheidungsproblem
Decision problem
Hilbert 1928
• Before the question could be answered, the
notion of "algorithm" had to be formally
defined.
– This was done by Alonzo Church in 1936 with the
concept of "effective calculability" based on his λ
calculus
– and by Alan Turing in the same year with his
concept of Turing machines.
– It was recognized immediately by Turing that
these are equivalent models of computation.

Alan Turing
(1912 – 1954)
Alonzo Church
(1903-1995)
Turing Machine Lambda calculus
Two mathematical ways to ask questions about
“computability”

Equivalent Computers
z z zz z z z
1
Start
HALT
), X, L
2:
look
for (
#, 1, -
), #, R
(, #, L
(, X, R
#, 0, -
Finite State Machine
...
Turing Machine

term = variable
| term term
| (term)
|  variable . term
y. M  v. (M [y v])
where v does not occur in M.
(x. M)N   M [ x N ]


Lambda Calculus

Alan Turing, 1936
• "On computable numbers, with an application
to the Entscheidungsproblem [decision
problem]”
• addressed a previously unsolved
mathematical problem posed by the German
mathematician David Hilbert in 1928:

Turing, 1936
Is there, in principal,
any definite mechanical method or process
by which
all mathematical questions
could be decided?
The Decision Problem

Turing, 1936
• To answer the question (in the negative),
• Turing proposed a simple abstract computing
machine,
• modeled after a mathematician with a pencil,
an eraser, and a stack of pieces of paper
• He asserted that any function is a computable
function if it is computable by one of these
abstract machines.

Turing, 1936
• He then investigated whether there were
some mathematical problems which could not
be solved by any such abstract machine.
• Such abstract computing machines are now
called "Turing machines".
• One particular Turing machine, called a
"Universal Turing Machine", served as the
model for designing actual programmable
computers.

Why a Turing Machine
Because Turing machines are very simple
compared with computers in practical use,
conceptually easier
to prove impossibility results
for Turing machines.
These impossibility results
apply as well to all known computers

Turing, 1936
• Startling result of Turing's 1936 paper
• assertion that there are well-defined
problems that cannot be solved by any
computational procedure.

What is Computable?
Computation is usually modelled as a mapping from inputs to outputs,
carried out by a formal “machine,” or program, which processes its
input in a sequence of steps.
An “effectively computable” function is one that can be computed in
a finite amount of time using finite resources.
…………
…………
…
input
yes
no
output
Effectively
computable
function

Unsolvable
• problems are formulated as functions
– unsolvable functions: noncomputable;
• Problems formulated as predicates
– Undecidable.
Using Turing's concept of the abstract machine,
we would say that a function is noncomputable
if there exists no Turing machine that could compute it.

TURING MACHINE
Computability
Functional Programming Turing Machine

............
Tape
Read-Write head
Control Unit

Turing Machine
............
Read-Write head
No boundaries -- infinite length
The head moves Left or Right
The
tape
OR
Functional Programming

Turing Machine
............
Read-Write head
The head at each time step:
1. Reads a symbol
2. Writes a symbol
3. Moves Left or Right

Turing Machine
............
Example:
Time 0
............
Time 1
a a cb
a b k c
1. Reads a
2. Writes k
3. Moves Left
a

Turing Machine
............
Time 1
a b k c
............
Time 2
a k cf
1. Reads b
2. Writes f
3. Moves Right
b

Add 1 to a sequence of ones
If 1, then move right If 1, then move left
Loop
If 0, replace with 1
Start: 0 0 0 1 1 1 1 0 0 0 4 ones in a row
End: 0 0 0 1 1 1 1 1 0 0 5 ones in a row

So what?
You can add a 1 to a sequence of ones
From a set of a few (a manageable number) of primitive operations
If a number is represented by a sequence of ones
then you have the x+1 operator, i.e addition
This is a/(the most) basic mathematical operator
Powerful enough to represent complex mathematics
You can derive other (all) mathematic operations and objects

Powerful “language”
From a set of a few (a manageable number) of
primitive operations
Easier enough
To formulate
Proofs about algorithms
Powerful enough
To
represent complex
mathematics
All the ingredients are there Only have to deal with a few basic operations
Not worried about complexity…. Worried about, for example, “can” we compute?

TURING MACHINE (PT 2)
Computability
Functional Programming Turing Machine (pt 2)

Turing Machine (pt 2)
The Input String
............    
Blank symbol
head
a b ca
Head starts at the leftmost position
of the input string
Input string

States & Transitions
1q 2qLba ,
Read Write Move Left
1q 2qRba ,
Move Right

Turing machine for the language }{ nn
ba
0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 ba
0q
a bTime 0 

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 bx
1q
a b Time 1

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 x
2q
a b Time 2 b

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
2q
a b Time 3

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
2q
a b Time 4

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
0q
a b Time 5

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
1q
x b Time 6

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
1q
x b Time 7

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx x y
2q
Time 8

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx x y
2q
Time 9

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
0q
x y Time 10

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
3q
x y Time 11

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
3q
x y Time 12

0q 1q 2q3q
Rxa ,
Raa ,
Ryy ,
Lyb ,
Laa ,
Lyy ,
Rxx ,
Ryy ,
Ryy ,
4q
L,
 yx
4q
x y 
Halt & Accept
Time 13

LAMBDA CALCULUS
Computability
Functional Programming Lambda Calculus

Lambda Calculus
Alonzo Church
(1903-1995)
Another formulation
of
computability

Equivalent Computers
z z zz z z z ...
Turing Machine

term = variable
| term term
| (term)
y. M  v. (M [y v])
where v does not occur in M.
(x. M)N   M [ x N ]


Lambda Calculus

What is Calculus?
• In High School:
d/dx xn = nxn-1 [Power Rule]
d/dx (f + g) = d/dx f + d/dx g [Sum Rule]
Calculus
is a branch of mathematics
that deals with limits
and the differentiation and
integration of functions
of one or more variables...

Real Definition
• A calculus is just a bunch of rules for
manipulating symbols.
• People can give meaning to those symbols,
but that’s not part of the calculus.
• Differential calculus is a bunch of rules for
manipulating symbols. There is an
interpretation of those symbols corresponds
with physics, slopes, etc.

-calculus
Alonzo Church, 1940
term = variable
| term term
| (term)

-calculus
 variable . term
F(variable) = term

Why?
• Once we have precise and formal rules for
manipulating symbols, we can use it to reason
with.
• Since we can interpret the symbols as
representing computations, we can use it to
reason about programs.

Universal Computer
• Lambda Calculus can simulate a Turing Machine
– Everything a Turing Machine can compute, Lambda
Calculus can compute also
• Turing Machine can simulate Lambda Calculus
– Everything Lambda Calculus can compute, a Turing
Machine can compute also
• Church-Turing Thesis: this is true for any other
mechanical computer also

Normal Steps
• Turing machine:
– Read one square on tape, follow one FSM
transition rule, write one square on tape, move
tape head one square
• Lambda calculus:
– One beta reduction
• Your PC:
– Execute one instruction (?)
• What one instruction does varies

-Reduction
(the source of all computation)
(x. M)N
This is the function definition
M is an expression with the variable x
N is used at the value of x
N substitutes x in the expression M

(x. x)a = a
-Reduction
(the source of all computation)
Identity operation
Function gives the argument as output
(x. xx)a = aa
(y.(x. xy)a)b =(y.ay)b=ab
(y.(x. xy) z.zy)b =(y.(z.zy)y)b
= (y. yy)b
=bb

-calculus
Useful and expression enough that a programming
language was modeled after it
LISP
was developed from -calculus
not the other way round.)
This was the “first” general language of
Artificial intelligence
Also
The “first” functional programming language

Expression Reductions
Reductions
are used in the lambda calculus to
reduce a statement to its simplest possible form.
This is, essentially, what a computation in lambda calculus does.
If you were to give a lambda calculus expression to "lambda
calculus" calculator,
it would use a combination of alpha, beta, and eta reductions
to find the simplest reduction of your expression.
https://classes.soe.ucsc.edu/cmps112/Spring03/readings/lambdacalculus/reductions.html

Expression Reduction
(𝛌x. x x) (𝛌y. y)
--> x x [𝛌y. y / x]
== (𝛌y. y) (𝛌y. y)
--> y [𝛌y. y / y]
== 𝛌y. y
How the original expression is
evaluated
Is determined the
operational semantics
of lambda calculus
(there are many ways to evaluate expressions)
Operational Semantics: how the substitutions are made:
Key concepts:
specification of free variables
specification of bound variables
Β-reduction
a formalization of simple substitution

Name Capture
Care must be taken
to avoid “name capture”
of bound variables.
For example, this reduction would be “wrong”:
(λx. (λy. x)) y ⇒ λy. y
because the outer y is presumably different
from the inner y bound by the lambda.
In cases like these, the bound variable is renamed to obtain the “correct” behavior:
(λx. (λy. x)) y ⇒ λz. y
http://www.cs.yale.edu/homes/hudak/CS201S08/lambda.pdf
Α-reduction is a formalization of renaming of variables
(without this, β-reduction can give the wrong answer)

EXAMPLES OF LAMBDA CALCULUS
Computability
Functional Programming Examples

syntax
• the identity function:
– 𝛌x.x
• 2 notational conventions:
• applications associate to the left (like in ML):
• “y z x” is “(y z) x”
• the body of a lambda extends as far as possible to the
right:
• “𝛌x.x 𝛌z.x z x” is “𝛌x.(x 𝛌z.(x z x))”

terminology
• 𝛌x.t
• 𝛌x.x y
the scope of x is the term t
(this is the part of the expression
where x can be substituted)
x is bound in the term 𝛌x.x y
(x is one of the variables that can be substituted)
y is free in the term 𝛌x.x y
(y is free to be substituted
into the expression .. In this case x)

Example
(λx. x x) (𝛌y. y)
--> x x [𝛌y. y / x]
== (𝛌y. y) (𝛌y. y)
--> y [𝛌y. y / y]
== 𝛌y. y
Substitute (𝛌y. y) into x
Substituted
Substitute (𝛌y. y) into y
Substituted

Another example
(𝛌x. x x) (𝛌x. x x)
--> x x [𝛌x. x x/x]
== (𝛌x. x x) (𝛌x. x x)
In other words,
it is simple to write non terminating computations
in the lambda calculus
what else can we do?
Substitute 𝛌x. x x into every x
The result is the same as the beginning

Computability, turing machines and lambda calculus

More Related Content

What's hot

Viewers also liked

Similar to Computability, turing machines and lambda calculus

More from Edward Blurock

Recently uploaded

Computability, turing machines and lambda calculus