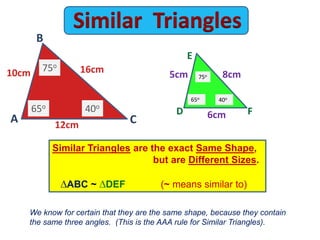
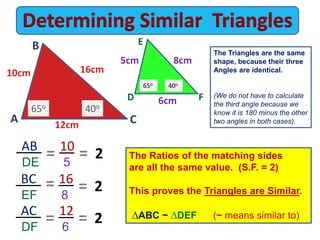
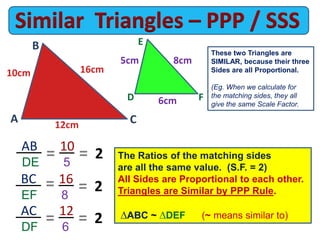
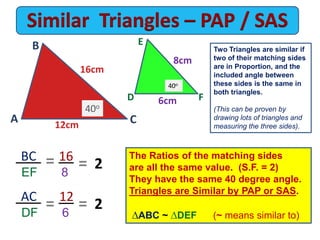
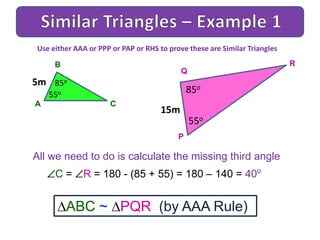
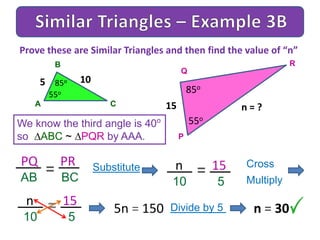
The document discusses similar triangles and scale factors. It provides examples of similar triangles in nature, art, architecture, and mathematics. It explains the different rules to determine if triangles are similar: AAA (angle-angle-angle), PPP (proportional property), PAP (proportional angles property), and RHS (right-hypotenuse-side). Examples are given applying these rules to prove triangles are similar and calculate missing side lengths or scale factors.

1. Tourmaline Crystals – Image Source: http://www.mnh.si.edu

2. When objects are the exact same shape,
but they are different sizes, we say that
they are “Similar” objects or figures.
Images from Google Images

3. When we double the Length and
Width of our Photo we ENLARGE
it using a SCALE FACTOR of 2.
When we halve the Length and
Width of our Photo we REDUCE
it using a SCALE FACTOR of 1/2.

4. If the SCALE FACTOR is Greater than 1
the resulting object is an ENLARGEMENT.
If the SCALE FACTOR is Less than 1
the resulting object is a REDUCTION.
Scale Factors less than 1 are expressed
as Fractions: ¼, ½, or as decimals: 0.3 etc
3
4
6
8

5. We calculate the SCALE FACTOR by
comparing matching sides, using Ratios.
We always Compare the New shape, with the
Original shape (Big vs Small for these Photos).
New 6 8
Old 3 4
3
4
6
8
= 2==
For our Photo Enlargement we have:
S.F. =

6. When we compare the Ratios of the
matching sides, we get “2” in both cases.
We say the two photos are “Similar” :
eg. Exact same shape, but different sizes.
New 16 9
Old 4 3
4
3
8
6
NOT ==
For Photo Enlargement 2 we have:
S.F. =
4
3
16
9
When the Ratios are not all the same,
the objects are not similar to each other.

7. We know for certain that they are the same shape, because they contain
the same three angles. (This is the AAA rule for Similar Triangles).
E
A
Similar Triangles are the exact Same Shape,
but are Different Sizes.
ABC ~ DEF (~ means similar to)
12cm
6cm
65o
65o
40o
40o
C
B
FD
16cm 8cm10cm 5cm
75o
75o

8. AC 12
DF 6
The Triangles are the same
shape, because their three
Angles are identical.
(We do not have to calculate
the third angle because we
know it is 180 minus the other
two angles in both cases).
AB 10
DE 5
E
A
= 2= The Ratios of the matching sides
are all the same value. (S.F. = 2)
This proves the Triangles are Similar.
ABC ~ DEF (~ means similar to)
12cm
6cm
65o
65o
40o
40o
C
B
FD
16cm
8cm
10cm
5cm
BC 16
EF 8
= 2=
= 2=

9. E
A
Similar Triangles are the exact Same Shape,
but are Different Sizes.
If two different triangles contain the exact
same angles, but are different sizes, then
they are similar. We call this the AAA Rule.
ABC ~ DEF (~ means similar to)
65o
65o
40o
40o
C
B
FD
75o
75o

10. AC 12
DF 6
These two Triangles are
SIMILAR, because their three
Sides are all Proportional.
(Eg. When we calculate for
the matching sides, they all
give the same Scale Factor.
AB 10
DE 5
E
A
= 2= The Ratios of the matching sides
are all the same value. (S.F. = 2)
All Sides are Proportional to each other.
Triangles are Similar by PPP Rule.
ABC ~ DEF (~ means similar to)
12cm
6cm
C
B
FD
16cm
8cm
10cm
5cm
BC 16
EF 8
= 2=
= 2=

11. AC 12
DF 6
Two Triangles are similar if
two of their matching sides
are in Proportion, and the
included angle between
these sides is the same in
both triangles.
(This can be proven by
drawing lots of triangles and
measuring the three sides).
E
A
The Ratios of the matching sides
are all the same value. (S.F. = 2)
They have the same 40 degree angle.
Triangles are Similar by PAP or SAS.
ABC ~ DEF (~ means similar to)
12cm
6cm
40o
40o
C
B
FD
16cm
8cm
BC 16
EF 8
= 2=
= 2=

12. E
A
If two different sized Right Triangles contain a 90
degree angle, and one matching side, as well
as the Hypotentuse are in the same Proportion,
then they are Similar by the RHS Rule.
ABC ~ DEF (~ means similar to)
C
B
F
D
8mm
4mm
10mm 5mm

13. Tourmaline Crystal cross sections contain Similar Triangles

14. Tourmaline is found in Mozambique, and is a gem used to
make spectacular jewellery such as these colorful cufflinks.

15. Similar Triangles can also be used to great effect in Art and
Craft, as seen in this colourful and creative patchwork quilt.
Image Source: http://www.patchworkpatterns.co.uk

16. Many Similar Triangles are present in this modern art piece.
Image Source: http://www.trianglesoflight.org

17. Many Similar Triangles are present in the structure of the
Sydney Harbour Bridge to give it strength and stability.
Image Source: Copyright 2012 Passy’s World of Mathematics

18. A
B
C
All we need to do is calculate the missing third angle
C = R = 180 - (85 + 55) = 180 – 140 = 40o
ABC ~ PQR (by AAA Rule)
Use either AAA or PPP or PAP or RHS to prove these are Similar Triangles
5m 85o
P
Q
R
15m
85o
55o
55o

19. Now we need to check the Ratios of the matching sides
C = F = 70o
ABC ~ DEF (by PAP or SAS Rule)
Use either AAA or PPP or PAP or RHS to prove these are Similar Triangles
A
B
C
8
70o
D
E
F
12
70o
3
4.5
DF 12
AC 8
= 1.5=
EF 4.5
BC 3
= 1.5=

20. A
B
C
We know the third angle is 40o
so ABC ~ PQR by AAA.
Prove these are Similar Triangles and then find the value of “n”
5 85o
P
Q
R
15
85o
55o
55o
10
n = ?
PQ 15
AB 5
= 3= This Scale Factor of S.F. = 3 tells us that
PQR is three times bigger than ABC.
Using the Scale Factor of 3:
n = 3 x 10 = 30

21. A
B
C
We know the third angle is 40o
so ABC ~ PQR by AAA.
Prove these are Similar Triangles and then find the value of “n”
5 85o
P
Q
R
15
85o
55o
55o
10
n = ?
PQ PR
AB BC
= Substitute n 15
10 5
= Cross
Multiply
n 15
10 5
= 5n = 150 Divide by 5 n = 30

22. A
B
C
We know the third angle is 40o
so ABC ~ PQR by AAA.
Prove these are Similar Triangles and then find the value of “k”
30
85o
P
Q
R
15
85o
55o
55o
10k = ?
PQ PR
AB BC
= Substitute 15 30
k 10
= Cross
Multiply
15 30
k 10
= 30k = 150 Divide by 30 k = 5

23. http://passyworldofmathematics.com/
All slides are exclusive Copyright of Passy’s World of Mathematics
Visit our site for Free Mathematics PowerPoints