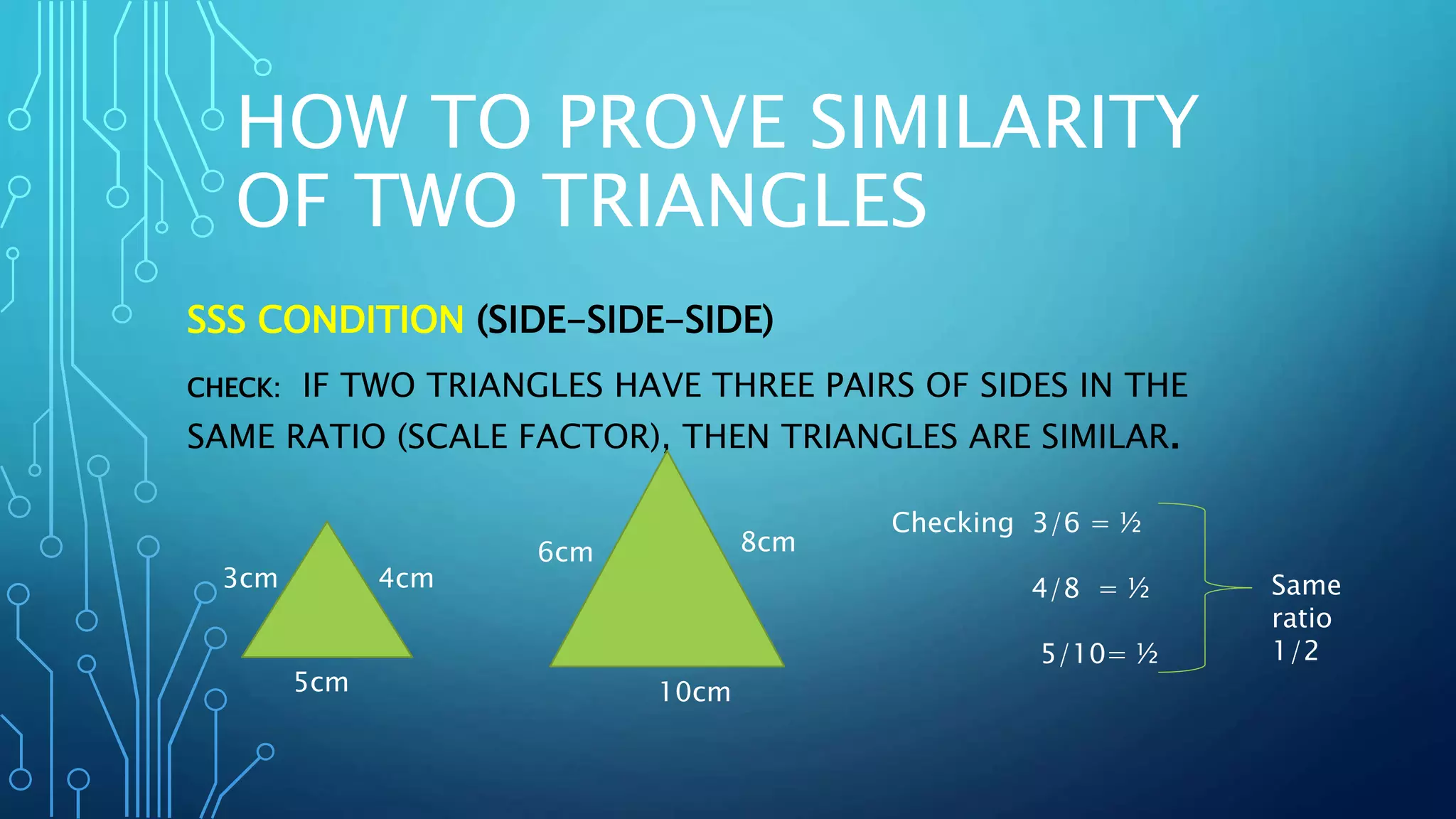
This document discusses how to prove that two triangles are similar. It provides three conditions to show similarity: SSS, where the ratios of all three pairs of corresponding sides are equal; AAA, where two or more pairs of corresponding angles are equal; and SAS, where the ratios of two pairs of corresponding sides are equal and the included angles are also equal. Examples are given for each condition to demonstrate how to check if two triangles are similar.

1. SIMILARITY (CLASS 10TH )
• When one shape can be changed into another after resizing, flipping,
sliding or turning. We can say two shapes are similar.
Properties of Similar Shapes
• In similar shapes, corresponding angles have the same measure.
• In similar shapes, the lengths of corresponding sides are proportional

2. HOW TO PROVE SIMILARITY
OF TWO TRIANGLES
SSS CONDITION (SIDE-SIDE-SIDE)
CHECK: IF TWO TRIANGLES HAVE THREE PAIRS OF SIDES IN THE
SAME RATIO (SCALE FACTOR), THEN TRIANGLES ARE SIMILAR.
3cm
5cm
4cm
6cm
10cm
8cm
Checking 3/6 = ½
4/8 = ½
5/10= ½
Same
ratio
1/2

3. HOW TO PROVE SIMILARITY OF TWO
TRIANGLES
AAA OR AA CONDITION (ANGLE- ANGLE- ANGLE)
CHECK : If two triangles have at least two of their angles equal, then
triangles are similar.
50
75
75
50
Checking:
Two angles are Same
50 and 75

4. HOW TO PROVE SIMILARITY OF TWO TRIANGLES
• SAS CONDITION (SIDE-ANGLE-SIDE)
Check If two triangles have two pairs of sides in the same ratio and the
included angles are also equal, then the triangles are similar.
Checking 5/10= ½
6cm 3/6 = ½
angle 30 (between sides)
3cm
5 cm
10cm
30
30