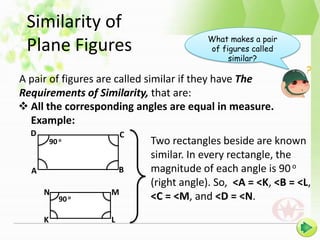
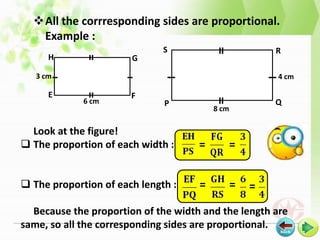
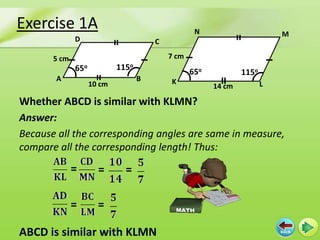
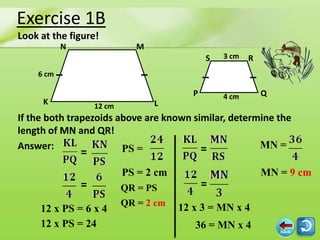
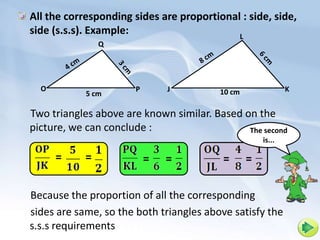
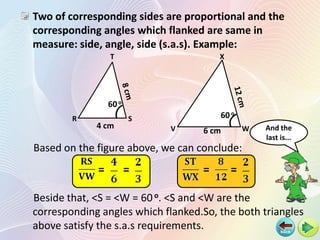
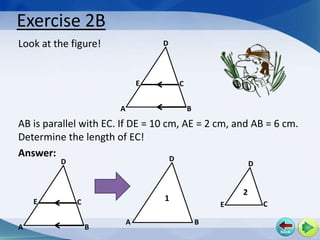
1) Two figures are similar if their corresponding angles are equal and their corresponding sides are proportional. 2) For triangles to be similar, either their corresponding angles must be equal (AAA), their corresponding sides must be proportional (SSS), or two corresponding sides and the included angle must be equal (SAS). 3) The document provides examples and exercises demonstrating similarity of figures and triangles.

1. Simila
rity
Cli
ck
thi
s!!
By :
Altafiyani
Rahmatika
Class : IX D

3. DEFINITION
Similarity is a pair of plane figures/plane objects
that are same in shape but different in size
(equivalent). Similarity is denoted by “~”

4. Similarity of
What makes a pair
Plane Figures of figures called
similar?
A pair of figures are called similar if they have The
Requirements of Similarity, that are:
 All the corresponding angles are equal in measure.
Example:
D C
90 o Two rectangles beside are known
similar. In every rectangle, the
A B magnitude of each angle is 90 o
(right angle). So, <A = <K, <B = <L,
N M
90 o <C = <M, and <D = <N.
K L

5. All the corrresponding sides are proportional.
Example :
S R
H G
3 cm 4 cm
E F
6 cm P Q
8 cm
Look at the figure!
 The proportion of each width : = =
 The proportion of each length : = = =
Because the proportion of the width and the length are
same, so all the corresponding sides are proportional.

6. Exercise 1A N M
D C
5 cm 7 cm
65o 115o
65o 115o
A B K
10 cm 14 cm L
Whether ABCD is similar with KLMN?
Answer:
Because all the corresponding angles are same in measure,
compare all the corresponding length! Thus:
= = =
= =
ABCD is similar with KLMN

7. Exercise 1B
Look at the figure!
N M
S 3 cm R
6 cm
P 4 cm Q
K 12 cm L
If the both trapezoids above are known similar, determine the
length of MN and QR!
Answer: PS = = MN =
=
PS = 2 cm MN = 9 cm
= QR = PS =
QR = 2 cm 12 x 3 = MN x 4
12 x PS = 6 x 4
12 x PS = 24 36 = MN x 4

8. Similarity of Triangles
Especially for triangles, two triangles called similar if they have
satisfy the following requirements:
All the corresponding angles are equal in measure : angle,
angle, angle (a.a.a). Example:
C Hello! I want to
H
explain about...
The first is...
50o 50o
90o 30o 90o
30o F G
A B
Two triangles above are known similar. Based on the
picture, we can conclude: <A = <F
<B = <G
<C = <H
So, the both triangles above satisfy the a.a.a requirements

9. All the corresponding sides are proportional : side, side,
side (s.s.s). Example: L
Q
O P J 10 cm K
5 cm
Two triangles above are known similar. Based on the
picture, we can conclude : The second
is...
= = = = = =
Because the proportion of all the corresponding
sides are same, so the both triangles above satisfy the
s.s.s requirements

10. Two of corresponding sides are proportional and the
corresponding angles which flanked are same in
measure: side, angle, side (s.a.s). Example:
T X
60 o
R S 60 o
4 cm V W And the
6 cm
last is...
Based on the figure above, we can conclude:
= = = =
Beside that, <S = <W = 60 o. <S and <W are the
corresponding angles which flanked.So, the both triangles
above satisfy the s.a.s requirements.

11. Exercise 2A
Which of these triangles that are similar?
G J
C
54o
8 cm 15 cm I
3 cm
54o 54o
A B E
5 cm
F H
Answer:
Use the third requirements of similarity in triangles (s.a.s) :
a. All of the corresponding angles which flanked are same in
measurement: <B = <E = <J = 54o
b. The proportion of all of the corresponding sides:
ABC and EFG :
= and =

12. EFG and HIJ :
= = and = =
ABC and HIJ : = = and =
So, the triangles
which are similar
are EFG and HIJ
or EFG ~HIJ

13. Exercise 2B
Look at the figure! D
E C
A B
AB is parallel with EC. If DE = 10 cm, AE = 2 cm, and AB = 6 cm.
Determine the length of EC!
Answer: D
D D
2
E C 1
E C
A B
A B

14. = =
12 x EC = 6 x 10
=
EC =
=
= = 5 cm
So, the length of EC is 5 cm.

15. Exercise 2C
Look at the figure!
Q
R OPQ is a right triangle and PR as
the altitude of OPQ. OR = 8 cm
and QR = 2 cm. Determine the
O P
length of PR!
P O
Answer: Q Because ROP is similar
R with RPQ, so:
Q R =
O
O P
R
PR2 = OR x QR
P
P PR =
PR =
PR =
P Q R PR = 4 cm