Uploaded byPassy World
Expanding Exponent Quotients
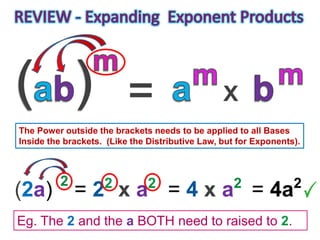
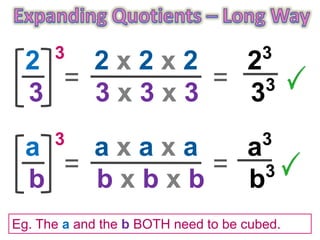
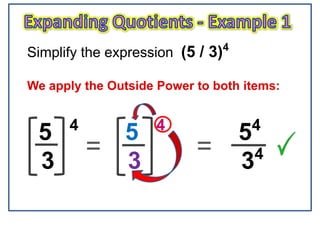
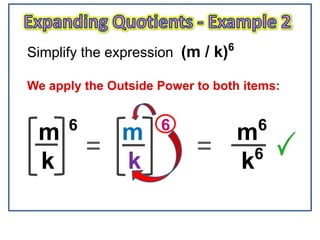
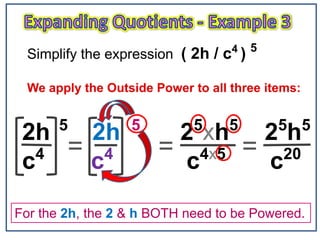
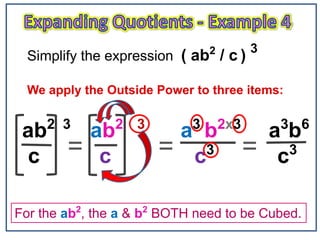
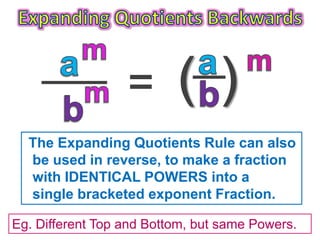
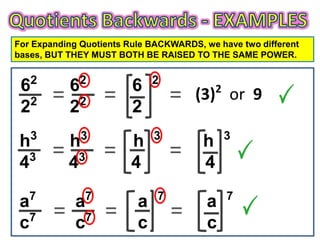
1) The document explains the expanding quotients rule for exponents, which involves applying the power outside of brackets to each term inside the brackets. 2) Examples show applying an exponent to terms like (2a), (a3/c), and (2h/c4) by raising both the numerical coefficient and variable to the same power outside the brackets. 3) The rule can also be used in reverse to combine identical exponents in a fraction into a single bracketed exponent expression.
More Related Content
Similar to Expanding Exponent Quotients
More from Passy World
Expanding Exponent Quotients
- 1.
- 2. Eg. The 2and the a BOTH need to raised to 2. The Power outside the brackets needs to be applied to all Bases Inside the brackets. (Like the Distributive Law, but for Exponents). (2a) 2 = 22 x a2 = 4 x a2 = 4a2
- 3. Eg. The aand the b BOTH need to be cubed. 2 3 2 x 2 x 2 23 3 3 x 3 x 3 33== a 3 a x a x a a3 b b x b x b b3==
- 4. Eg. The aand the b BOTH need to be Powered. The Expanding Quotients Rule involves applying the Power Outside of the brackets, onto every item that is inside the brackets.
- 5. 5 4 5 4 54 33 34 Simplify the expression (5 / 3)4 We apply the Outside Power to both items: ==
- 6. m 6 m 6 m6 kk k6 Simplify the expression (m / k)6 We apply the Outside Power to both items: ==
- 7. 2h 5 2h 5 25 xh5 25 h5 c4 c4 c4x5 c20 Simplifythe expression ( 2h / c4 ) 5 We apply the Outside Power to all three items: == = For the 2h, the 2 & h BOTH need to be Powered.
- 8. ab2 3 ab2 3 a3 b2x3 a3 b6 cc c3 c3 Simplify the expression ( ab2 / c ) 3 We apply the Outside Power to three items: == = For the ab2 , the a & b2 BOTH need to be Cubed.
- 9. Eg. Different Topand Bottom, but same Powers. The Expanding Quotients Rule can also be used in reverse, to make a fraction with IDENTICAL POWERS into a single bracketed exponent Fraction.
- 10. For Expanding QuotientsRule BACKWARDS, we have two different bases, BUT THEY MUST BOTH BE RAISED TO THE SAME POWER. 62 62 6 2 22 22 2 = = = (3)2 or 9 h3 h3 h 3 h 3 43 43 4 4 = = = a7 a7 a 7 a 7 c7 c7 c c = = =
- 11. http://passyworldofmathematics.com Visit our Sitefor Free Mathematics PowerPoints